\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
円柱まわりの低レイノルズ数流れ (渦度法)
広い領域に置かれた円柱(無限の高さ)の軸に垂直に一様流が当たっている。
この場合の流れを、非定常の方程式を定常になるまで解くことによって解く。
円柱から遠ざかるほど、流れは一様流に近づき変化は少なくなるので、格子は粗くてよい。
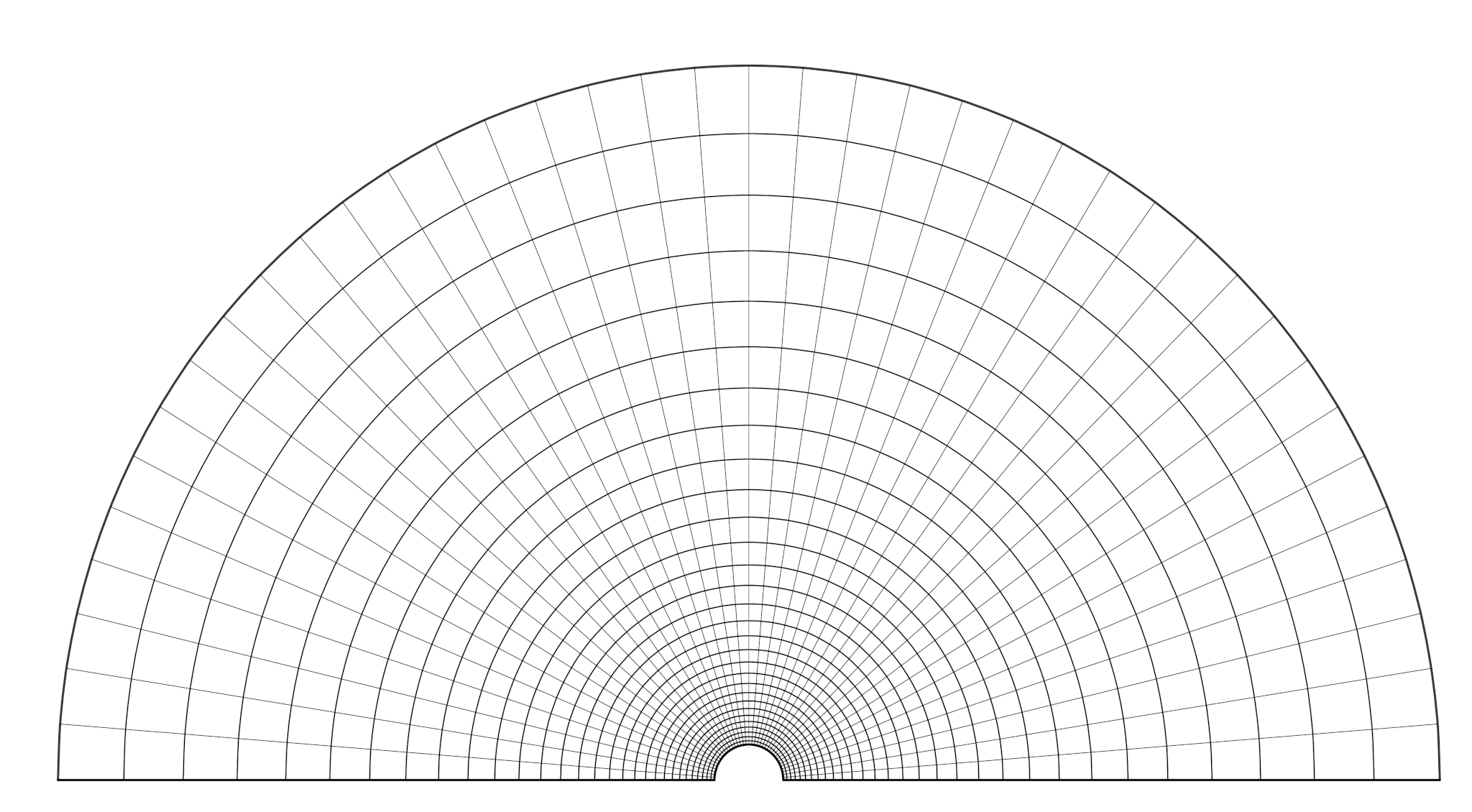
したがって、座標軸の動径方向に\( \,r=e^{\,\xi}\,\)という変換を施した。
メッシュは左図のようになる。
返還式は次のようになる。
\(\quad\left\{\begin{array}{l}x=e^{\,\xi}\cos\theta\\
y=e^{\,\xi}\sin\theta\qquad\cdots\,(1)\end{array}\right.\)
極座標の$\,\theta=0\,$の方向から一様流が当たるとするので、図の右からとなる。
式(1)から流れ関数-渦度法の基礎方程式は
\(\quad\left\{\begin{array}{l}\ppdr{\phi}{\xi^2}+\ppdr{\phi}{\theta^2}=-\omega\,e^{\,2\xi}\hspace{75mm}\cdots\,(2)\\
\pdr{\omega}{t}+e^{-2\xi}\left(\pdr{\phi}{\theta}\,\pdr{\omega}{\xi}-\pdr{\phi}{\xi}\,\pdr{\omega}{\theta}\right)=\dfrac{e^{-2\xi}}{\mathrm{Re}}\left(\ppdr{\omega}{\xi^2}+\ppdr{\omega}{\theta^2}\right)\qquad\cdots\,(3)\end{array}\right.\)
ここで、\(\omega\,,\,\phi\,\)は以下のように定義される。
\(\quad\omega=\pdr{v}{x}-\pdr{u}{y}\quad\cdots\,(4)\qquad u=\pdr{\phi}{y}\quad\cdots\,(5)\qquad v=-\pdr{\phi}{x}\quad\cdots\,(6)\)
この関係から、流れ関数と極座標における速度成分関係式が導かれる。
\(\quad\left\{\begin{array}{l}v_r=\dfrac{1}{r}\,\pdr{\phi}{\theta}=e^{-\,\xi}\pdr{\phi}{\theta}\hspace{20mm}\cdots\,(7)\\
v_{\theta}=-\pdr{\phi}{r}=-e^{-\,\xi}\pdr{\phi}{\xi}\hspace{18mm}\cdots\,(8)\end{array}\right.\)
◆ 計算
計算では、極座標の \(0\,\le\theta\,\lt\,\pi\,\)の範囲で計算し、反対側は\(\,x\,\)軸で折り返す形でコピーする事とする。
・流れ関数の境界条件
\(\quad\phi=0\hspace{30mm}\)(対称線、円柱上)
\(\quad\phi=y=e^{\,\xi}\sin\theta\hspace{25mm}\)(遠方)
・渦度の境界条件
\(\quad\omega=0\hspace{30mm}\)(遠方、対称線)
\(\quad\omega=-e^{-2\,\xi}\ppdr{\phi}{\xi^2}\quad\to\quad \omega_0=-2\phi_P\,/\,(\Delta\xi)^2\qquad\)(円柱上)
・初期条件
\(\quad\left\{\begin{array}{l}\phi=(r-(1/r))\sin\theta=(e^{\,\xi}-e^{-\,\xi})\sin\theta\\
\omega=0\end{array}\right.\hspace{40mm}\)(全域)
◆ 参考文献
- 流体解析の基礎:河村 哲也(2014)、朝倉書店
# 円柱まわりの低レイノルズ数流れ(渦度法)
#
import numpy as np
from matplotlib import pyplot as plt
import japanize_matplotlib
import warnings
# 警告非表示
warnings.simplefilter('ignore')
# ------- 条件設定
na = 40
ny = 42
nx = na * 2
nxc = na-1
nyc = ny-1
re = 40. # レイノルズ数
r1 = 1./re
dy = 0.05 # 半径の刻み幅
dt = 0.01 # 時間刻み
td = 1./dt
lmax = 2000 # 繰り返し計算回数
km = 40 # SOR法の最大反復回数
const = 1.0 # SOR法の加速係数
eps = 0.0001 # 繰り返し演算打ち切り誤差
dx = np.pi/float(na)
dxi = 1./dx
dyi = 1./dy
dx2 = dxi*dxi
dy2 = dyi*dyi
fct = .5/(dx2+dy2)
# --------- 配列初期化
psi=np.zeros((ny,na)) # ψ
omg=np.zeros((ny,na)) # ω
tmp=np.zeros((ny,na)) # ωバックアップ
u=np.zeros((ny,nx)) # 流速 u
v=np.zeros((ny,nx)) # 流速 v
omgd=np.zeros((ny,nx)) # ω表示用
# -------- 極座標
th = np.linspace(0, 2*np.pi,nx)
r = np.zeros(ny)
for j in range(nyc):
r[j+1]=np.exp(j*dy)
TH,R=np.meshgrid(th,r)
#print("th",th)
#print("r=",r)
# --- 初期条件
for i in range(na): # r 方向の最内側は円筒部分
psi[0][i]=0
omg[0][i]=0
u[0][i]=0
v[0][i]=0
for j in range(1,ny):
for i in range(na):
psi[j][i]=r[j]*np.sin(th[i]) # 遠方 e^ξ sin θ
# ----- 【 メインループ 】------
#
for l in range(1,lmax+1):
fff=(l-1)/30.
if fff>= 1.:
fff=1.
# STEP 1 境界条件
for i in range(na):
omg[1][i]=-2.*psi[2][i]*dy2*fff # 円筒上
psi[1][i]=0. # φ=0
for i in range(na):
psi[nyc][i]=r[nyc]*np.sin(th[i]) # 遠方
omg[nyc][i]=0.
for j in range(ny): # 対称線上
psi[j][0]=0.
omg[j][0]=0.
psi[j][nxc]=0.
omg[j][nxc]=0.
# STEP2 ポアソン方程式を解いて ψ を求める
for k in range(1,km):
err=0.
for j in range(2,nyc):
for i in range(1,nxc):
psx2=(psi[j][i+1]+psi[j][i-1])*dx2
psy2=(psi[j+1][i]+psi[j-1][i])*dy2
rhs=(psx2+psy2+omg[j][i]*np.exp(2.*j*dy))*fct
err=err+(rhs-psi[j][i])*(rhs-psi[j][i])
psi[j][i]=psi[j][i]*(1.-const)+rhs*const
if err < 0.00001:
break;
# STEP3 ω の時間発展を求める
for j in range(2,nyc):
for i in range(1,nxc):
tmp[j][i]=omg[j][i]
omx2=(omg[j][i+1]-2.*omg[j][i]+omg[j][i-1])*dx2
omy2=(omg[j+1][i]-2.*omg[j][i]+omg[j-1][i])*dy2
psx=(psi[j][i+1]-psi[j][i-1])*.5*dxi
psy=(psi[j+1][i]-psi[j-1][i])*.5*dyi
omx=(omg[j][i+1]-omg[j][i-1])*.5*dxi
omy=(omg[j+1][i]-omg[j-1][i])*.5*dyi
rhs=((omx2+omy2)*r1+psx*omy-psy*omx)*np.exp(-2.*j*dy)
omg[j][i]=omg[j][i]+dt*rhs
# STEP4 誤差のチェック
err1=0.
for j in range(2,nyc):
for i in range(1,nxc):
bb = np.abs(omg[j][i]-tmp[j][i])
if bb>=err1:
err1=bb
if l>10 and err1<=eps:
break;
# 結果の表示
print( "loop=",l,"(time=",l*dt,") err1=",'{:.2e}'.format(err1))
for j in range(2,nyc):
for i in range(1,nxc):
# vth=-(psi[j][i+1]-psi[j][i-1])*.5*dxi/r[j]
vth=-(psi[j][i+1]-psi[j][i-1])*.5*dxi/r[j]+np.pi
vrs=(psi[j+1][i]-psi[j-1][i])*.5*dyi/r[j]
vth2=2.*np.pi-vth
u[j][i]=vrs*np.cos(vth)
u[j][nx-i]=vrs*np.cos(vth2)
v[j][i]=vrs*np.sin(vth)
v[j][nx-i]=vrs*np.sin(vth2)
omgd[j][i]=omg[j][i]
omgd[j][nx-i]=omg[j][i]
fig=plt.figure(figsize=(10,10))
ax1 = plt.subplot(111, polar=True)
ax1.set_title('流れ',fontsize=25)
ax1.quiver(TH,R,u,v,color='blue')
ax1.axis('off')
plt.show()
fig=plt.figure(figsize=(10,10))
ax2 = plt.subplot(111, polar=True)
ax2.set_title('ω(渦度)',fontsize=26)
#ax2.contourf(TH,R,omgd,cmap='autumn_r')
ax2.contourf(TH,R,omgd,cmap='PuBu_r')
ax2.axis('off')
plt.show()
loop= 2000 (time= 20.0 ) err1= 2.67e-04