\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
◆ はじめに
非圧縮性の流れ方程式は、連続の式とナビエストークス方程式(無次元化した)を連立して解くことになる。
\(\left\{\begin{array}{l}\nabla\cdot\bm{V}=0\hspace{53mm}\cdots\,(1)\\
\pdr{\bm{V}}{t}+(\bm{V}\cdot\nabla)\bm{V}=-\nabla p+\dfrac{1}{\mathrm{Re}}\Delta\bm{V}\qquad\cdots\,(2)\end{array}\right.\)
この方程式は非線形で、かつ速度\(\,\bm{V}\,\)については時間発展形になっているが、圧力\(\,p\,\)についてはそうなっていない。そこで、速度\(\,\bm{V}\,\)を時間発展的に求める場合、各時間ステップでの連続の式(式(1))を満足するように圧力\(\,p\,\)を求める必要がある。
非圧縮性ナビエストークス方程式を数値的に解く方法はいくつかあるが、ここでは圧力を消去する渦度法をここで説明する。
◆ 導出
式(1)(2)を2次元で表すと
\(\left\{\begin{array}{l}\pdr{u}{x}+\pdr{v}{y}=0\hspace{40mm}\cdots\,(3)\\
\pdr{u}{t}+u\pdr{u}{x}+v\pdr{u}{y}=-\pdr{p}{x}+\dfrac{1}{\mathrm{Re}}\left(\ppdr{u}{x^2}+\ppdr{u}{y^2}\right)\qquad\cdots\,(4)\\
\pdr{v}{t}+u\pdr{v}{x}+v\pdr{v}{y}=-\pdr{p}{y}+\dfrac{1}{\mathrm{Re}}\left(\ppdr{v}{x^2}+\ppdr{v}{y^2}\right)\qquad\,\cdots\,(5)\end{array}\right.\)
まず、式(4)を\(\,y\,\)で偏微分する。左辺は
\(\quad\pdr{}{t}\left(\pdr{u}{y}\right)+\pdr{u^2}{x\,\partial y}+u\,\ppdr{u}{x\,\partial y}+\pdr{v}{y}\pdr{u}{y}+v\,\ppdr{u}{y^2}\qquad\)となる。変形すると
\(\quad=\pdr{}{t}\left(\pdr{u}{y}\right)+u\,\ppdr{u}{x\,\partial y}+\pdr{u}{y}\left(\pdr{u}{x}+\pdr{v}{y}\right)+v\,\ppdr{u}{y^2}\qquad\)式(3)を代入すると
\(\quad=\pdr{}{t}\left(\pdr{u}{y}\right)+u\,\ppdr{u}{x\,\partial y}+v\,\ppdr{u}{y^2}\qquad\cdots\,(6)\quad\)となる。
右辺は
\(\quad -\ppdr{p}{x\,\partial y}+\dfrac{1}{\mathrm{Re}}\,\pdr{}{y}\left(\ppdr{u}{x^2}+\ppdr{u}{y^2}\right)\qquad\cdots\,(7)\quad\)となる。
続けて、式(5)を\(\,x\,\)で偏微分する。左辺は式(4)と同様に変形すると
\(\quad\pdr{}{t}\left(\pdr{v}{x}\right)+u\,\ppdr{v}{x^2}+v\,\ppdr{v}{x\,\partial y}\qquad\cdots\,(8)\quad\)となる。
右辺は
\(\quad -\ppdr{p}{x\,\partial y}+\dfrac{1}{\mathrm{Re}}\,\pdr{}{x}\left(\ppdr{v}{x^2}+\ppdr{v}{y^2}\right)\qquad\cdots\,(9)\quad\)となる。
ここで、式(8)から式(6)を引いて偏微分の順序を入れ替えると
\(\quad\pdr{}{t}\left(\pdr{v}{x}-\pdr{u}{y}\right)+u\,\pdr{}{x}\left(\pdr{v}{x}-\pdr{u}{y}\right)+v\,\pdr{}{y}\left(\pdr{v}{x}-\pdr{u}{y}\right)\qquad\cdots\,(10)\quad\)となる。
式(9)から式(7)を引くと
\(\quad\dfrac{1}{\mathrm{Re}}\left(\pdr{}{x}\ppdr{v}{x^2}+\pdr{}{x}\ppdr{v}{y^2}-\pdr{}{y}\ppdr{u}{x^2}-\pdr{}{y}\ppdr{u}{y^2}\right)\)
\(\quad=\dfrac{1}{\mathrm{Re}}\left(\ppdr{}{x^2}\pdr{v}{x}+\ppdr{}{y^2}\pdr{v}{x}-\ppdr{}{x^2}\pdr{u}{y}-\ppdr{}{y^2}\pdr{u}{y}\right)\)
\(\quad=\dfrac{1}{\mathrm{Re}}\left[\ppdr{}{x^2}\left(\pdr{v}{x}-\pdr{u}{y}\right)+\ppdr{}{y^2}\left(\pdr{v}{x}-\pdr{u}{y}\right)\right]\qquad\cdots\,(11)\quad\)となる。
ここで渦度\(\,\omega\,\)を流速ベクトル\(\,\bm{V}\,\)の回転とする。
\(\quad\omega=\nabla\times\bm{V}=\pdr{v}{x}-\pdr{u}{y}\hspace{40mm}\cdots\,(12)\)
この式(12)を式(10)と式(11)に代入して等号で結ぶと
\(\quad\pdr{\omega}{t}+u\,\pdr{\omega}{x}+v\,\pdr{\omega}{y}=\dfrac{1}{\mathrm{Re}}\left(\ppdr{\omega}{x^2}+\ppdr{\omega}{y^2}\right)\qquad\cdots\,(13)\)
流れ関数\(\,\phi(x,y)\,\)を考える。流速ベクトルを流れ関数の回転と定義する。
\(\quad\bm{V}=\nabla\times\,(0,0,\phi)=\left(\pdr{\phi}{y}\,,\,-\pdr{\phi}{x}\,,\,0\right)\qquad\cdots\,(14)\)
2次元の場合、\(\bm{V}=(\,u\,,\,v\,,\,0)\,\)の渦度の\(\,z\,\)成分\(\,\omega\,\)は
\(\quad\omega=\pdr{v}{x}-\pdr{u}{y}=-\left(\ppdr{\phi}{x^2}+\ppdr{\phi}{y^2}\right)\qquad\cdots\,(15)\)
よって、式(1)(2)は流れ関数\(\,\phi\,\)と渦度\(\,\omega\,\)の連立方程式として、以下の形になる。
\(\left\{\begin{array}{l}\ppdr{\phi}{x^2}+\ppdr{\phi}{y^2}=-\omega\hspace{60mm}\cdots\,(16)\\
\pdr{\omega}{t}+\pdr{\phi}{y}\,\pdr{\omega}{x}-\pdr{\phi}{x}\,\pdr{\omega}{y}=\dfrac{1}{\mathrm{Re}}\left(\ppdr{\omega}{x^2}+\ppdr{\omega}{y^2}\right)\qquad\cdots\,(17)\end{array}\right.\)
◆ 解き方
式(16)、(17)を差分近似する。差分については「差分について」を参照のこと。
\(\quad a_2\phi_{i-1,j}+b_2\phi_{i,j}+c_2\phi_{i+1,j}+a_4\phi_{i,j-1}+b_4\phi{i,j}+c_4\phi_{i,j+1}=-\omega_{i,j}\qquad\cdots\,(18)\)
\(\quad\dfrac{\omega_{i,j}^{n+1}-\omega_{i,j}}{\Delta t}+(a_3\phi_{i,j-1}+b_3\phi_{i,j}+c_3\phi_{i,j+1})(a_1\omega_{i-1,j}+b_1\omega_{i,j}+c_1\omega_{i+1,j})\)
\(\hspace{28mm}-(a_1\phi_{i-1,j}+b_1\phi{i,j}+c_1\phi_{i+1,j})(a_3\omega_{i,j-1}+b_3\omega_{i,j}+c_3\omega_{i,j+1})\)
\(\hspace{15mm}=\dfrac{1}{\mathrm{Re}}(a_2\omega_{i-1,j}+b_2\omega_{i,j}+c_2\omega_{i+1,j}+a_4\omega_{i,j-1}+b_4\omega_{i,j}+c_4\omega_{i,j+1})\qquad\cdots\,(19)\)
まず、式(18)をSOR法(参照)で解くために、式(18)を\(\,\phi_{i,j}\,\)について解いて
\(\quad\phi_{i,j}^*=-\dfrac{1}{b_2+b_4}(a_2\phi_{i-1,j}^{(\nu+1)}+c_2\phi_{i+1,j}^{(\nu)}+a_4\phi_{i,j-1}^{(\nu+1)}+c_4\phi_{i,j+1}^{(\nu)}+\omega_{i,j})\qquad\cdots\,(20)\)
\(\quad\phi_{i,j}^{(\nu+1)}=(1-\alpha)\phi_{i,j}^{(\nu)}+\alpha\phi_{i,j}^*\qquad\cdots\,\,(21)\)
として、反復解法(SOR法)で求める。ただし、\(\,\nu\,\)は反復回数、\(\,\alpha\,\)は加速係数である。
◆ 参考文献
- 流体解析の基礎:河村 哲也(2014)、朝倉書店
- 流体力学第2版:杉山 弘、遠藤 剛、新井 隆景(2014)、森北出版
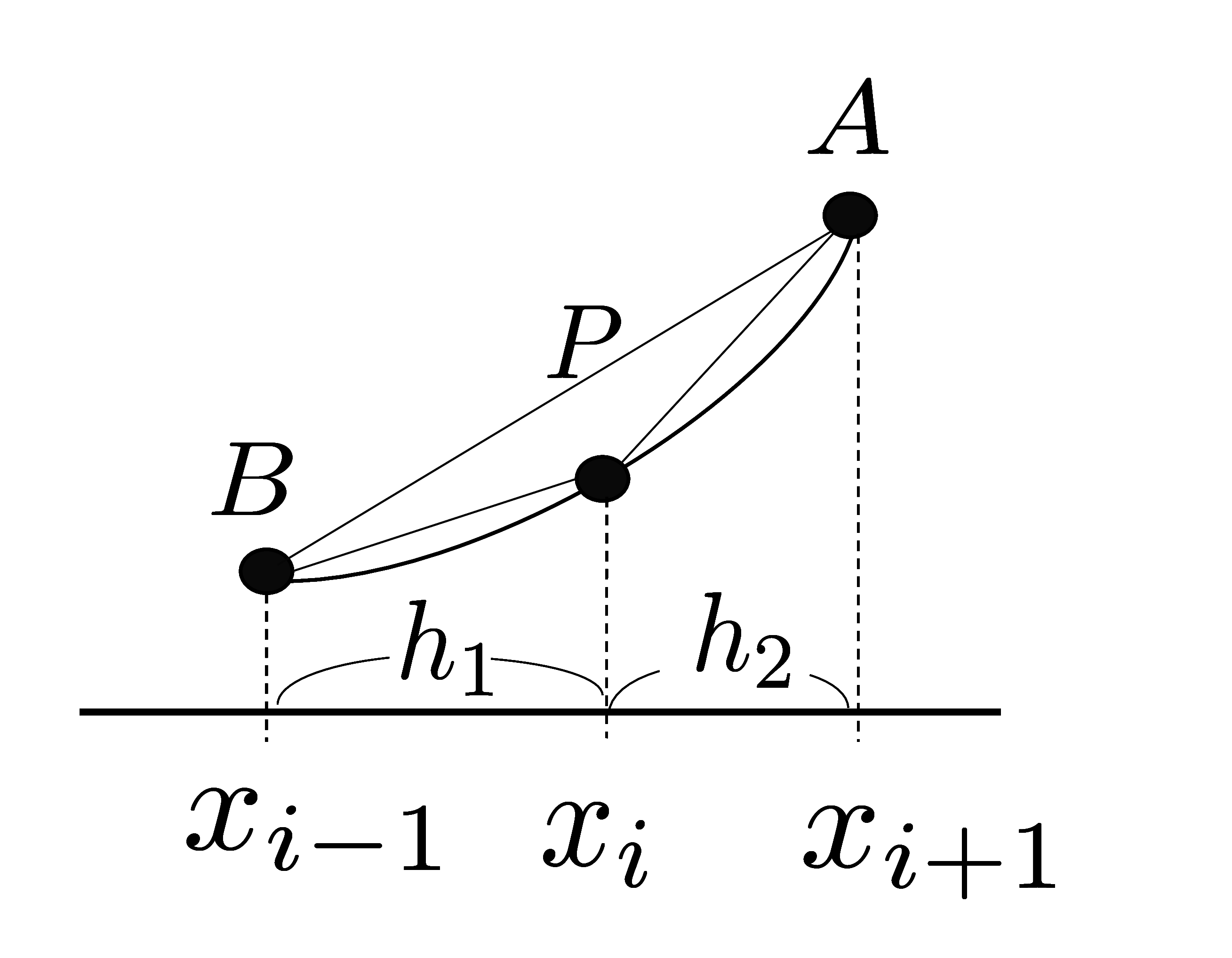 関数 \(f(x)\,\)の\(\,x=x_i\,\)における微分は
関数 \(f(x)\,\)の\(\,x=x_i\,\)における微分は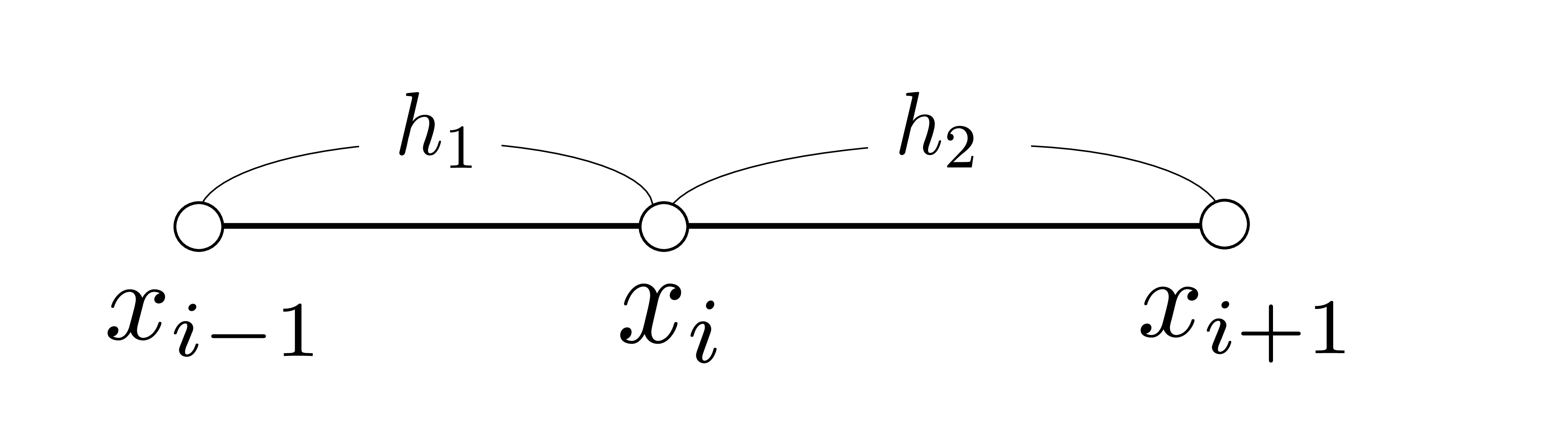 左図のような\(\,h_1\ne h_2\,\)の場合、不均等格子となる。三点の線形結合で微分を差分で表すことを考える。\(\,f(x_i)\,\)を\(\,f_i\,\)と表すこととする。
左図のような\(\,h_1\ne h_2\,\)の場合、不均等格子となる。三点の線形結合で微分を差分で表すことを考える。\(\,f(x_i)\,\)を\(\,f_i\,\)と表すこととする。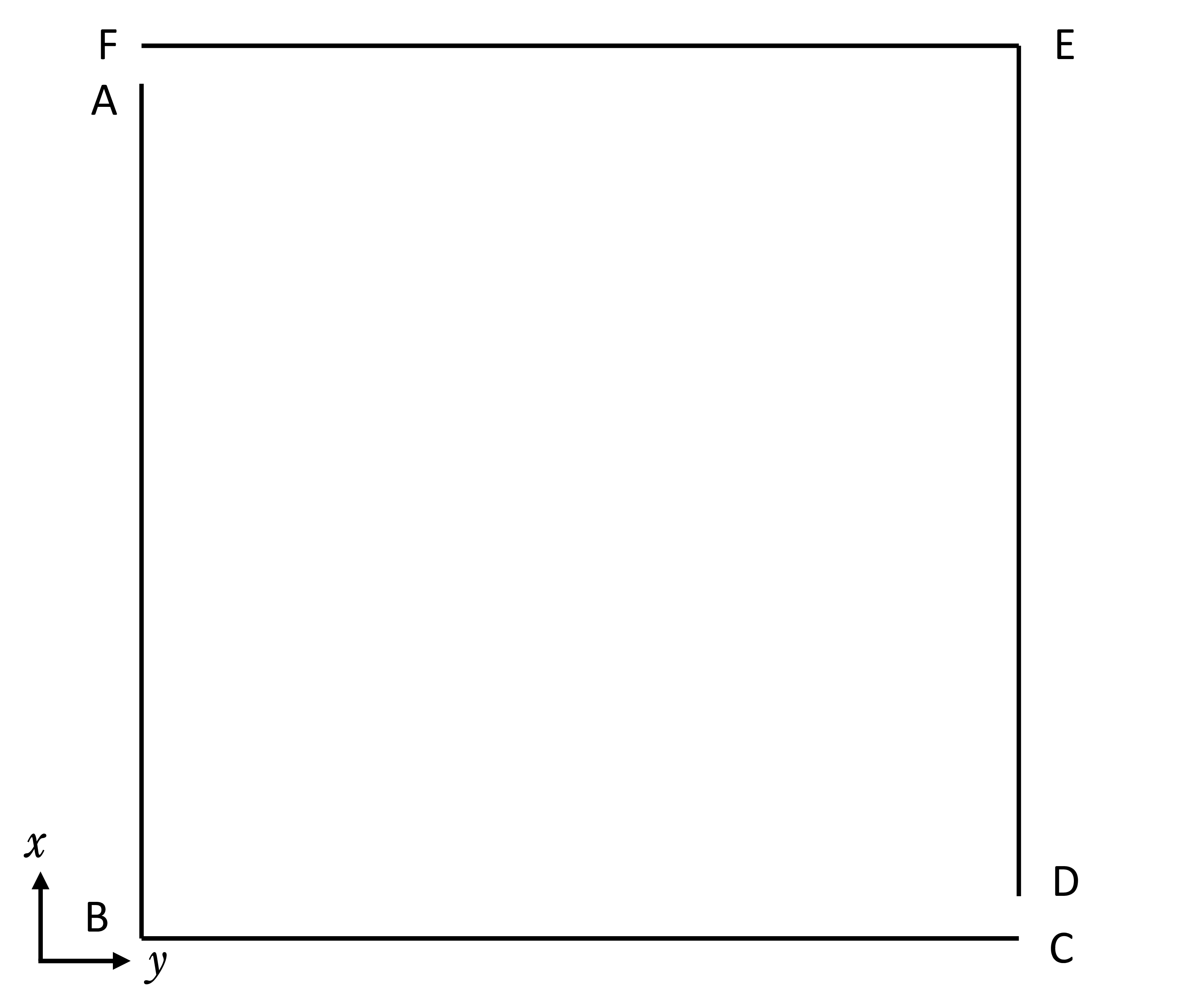 不均等格子を用いて、室内気流の層流解析を行う。河村先生の「流体解析の基礎」を参考にした。
不均等格子を用いて、室内気流の層流解析を行う。河村先生の「流体解析の基礎」を参考にした。
 小さい流入や流出口の場合、ある程度の格子点を集める必要がある。このような場合は、流出流入口周りに格子点を集めるような不均等格子を用いる。今回は左の図のような格子を使用した。
小さい流入や流出口の場合、ある程度の格子点を集める必要がある。このような場合は、流出流入口周りに格子点を集めるような不均等格子を用いる。今回は左の図のような格子を使用した。