\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
自然対流では運動方程式に浮力(重力)による外力が加わる。
\(\quad\pdr{\bm{V}}{t}+(\bm{V}\cdot\nabla)\bm{V}=-\dfrac{1}{\rho}\nabla\bm{V}+\dfrac{\mu}{\rho}\Delta\bm{V}+\bm{g}\qquad\cdots\,(1)\)
2次元問題として考える。重力の方向を\(\,y\,\)方向下方にとる。温度\(\,T\,\)、熱量\(\,Q\,\)を無次元化すると以下の方程式が得られる。
\(\left\{\begin{array}{l}\pdr{u}{x}+\pdr{v}{y}=0\hspace{86mm}\cdots\,(2)\\
\pdr{u}{t}+u\,\pdr{u}{x}+v\,\pdr{u}{y}=-\pdr{p}{x}+\dfrac{1}{\mathrm{Re}}\left(\ppdr{u}{x^2}+\ppdr{u}{y^2}\right)\hspace{23mm}\cdots\,(3)\\
\pdr{v}{t}+u\,\pdr{v}{x}+v\,\pdr{v}{y}=-\pdr{p}{y}+\dfrac{1}{\mathrm{Re}}\left(\ppdr{v}{x^2}+\ppdr{v}{y^2}\right)+\dfrac{\mathrm{Gr}}{\mathrm{Re}^2}\,T\hspace{6mm}\cdots\,(4)\\
\pdr{T}{t}+u\,\pdr{T}{x}+v\,\pdr{T}{y}=\dfrac{1}{\mathrm{Re}\,\mathrm{Pr}}\left(\ppdr{T}{x^2}+\ppdr{T}{y^2}\right)+Q\hspace{21mm}\cdots\,(5)
\end{array}\right.\)
ここで、\(\mathrm{Gr}\,,\,\mathrm{Pr}\,\)はそれぞれグラスホフ数、プラントル数と呼ばれる無次元数である。(流れ関係特性値参照)
ここに、『渦度法』を適用すると、
\(\left\{\begin{array}{l}\ppdr{\phi}{x^2}+\ppdr{\phi}{y^2}=-\omega\hspace{80mm}\cdots\,(6)\\
\pdr{\omega}{t}+\pdr{\phi}{y}\,\pdr{\omega}{x}-\pdr{\phi}{x}\,\pdr{\omega}{y}=\dfrac{1}{\mathrm{Re}}\left(\ppdr{\omega}{x^2}+\ppdr{\omega}{y^2}\right)+\dfrac{\mathrm{Gr}}{\mathrm{Re}^2}\,\pdr{T}{x}\hspace{5mm}\cdots\,(7)\\
\pdr{T}{t}+\pdr{\phi}{y}\,\pdr{T}{x}-\pdr{\phi}{x}\,\pdr{T}{y}=\dfrac{1}{\mathrm{Re}\,\mathrm{Pr}}\left(\ppdr{T}{x^2}+\ppdr{T}{y^2}\right)\hspace{24mm}\cdots\,(8)\end{array}\right.\)
ここで、\(\omega\,\,,\,\phi\,\)は、渦度および流れ関数で、次式で定義される。
\(\quad\omega=\pdr{v}{x}-\pdr{u}{y}\quad ,\qquad u=\pdr{\phi}{y}\quad ,\qquad v=-\pdr{\phi}{x}\qquad\cdots\,(9)\)
◆ 計算モデル
以下のような条件を設定する。
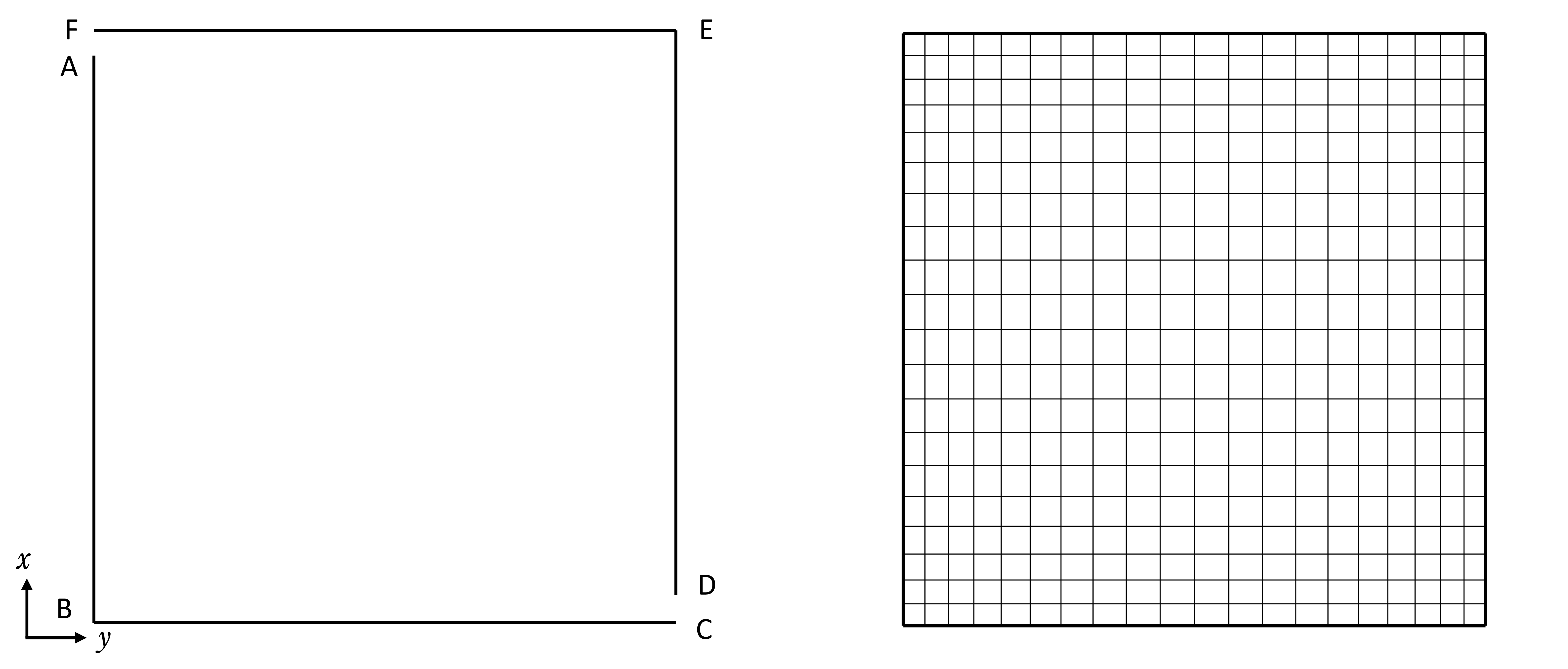
左図のような矩形領域で、FA が入口、DC が出口である。メッシュは右図のような周辺部の分割が細かい不均等格子とする。
境界条件
\(\quad \phi=\di\int_{y_A}^y\,u\,dy\qquad \)として\(\quad u=1\,\)とすると\(\quad \phi=y-y_A\quad\)(AF上)となる。
\(\quad\)ここで、壁面 DEF と ABC の流れ関数の差を\(\,q\,\)とすると、\(\,q=y_F-y_A\,\)となる。
\(\quad\)CD上での\(\,y\,\)方向速度\(\,v=0\,\)と仮定すると、\(\phi_P=\phi_Q\,\)(CD上) という条件となる。
\(\quad\)流入口 AF で渦なし一様流が流入するとすると\(\quad\omega=0\,\)。
\(\quad\)流出条件としては一応このような条件を設定する。\(\quad\omega_P=\omega_Q\)
\(\quad T=T_{wall}\,\,\)(BC上)とし、\(\partial T/\partial x=0\,\,\,\)(AB,DE上)、\(\partial t/\partial y=0\,\,\,\)(CD上)
\(\quad t=T_0\,\,\)(AF上)、\(\partial t/\partial x=0\,\,\,\)(CD上)および、\(\,T_P=T_Q\,\)の条件とする。
◆ 参考文献
- 流体解析の基礎:河村 哲也(2014)、朝倉書店
- 流体力学第2版:杉山 弘、遠藤 剛、新井 隆景(2014)、森北出版
# 室内換気 不定形格子(渦度法)
#
import numpy as np
from matplotlib import pyplot as plt
import japanize_matplotlib
import warnings
# 警告非表示
warnings.simplefilter('ignore')
# ------- 条件設定
nx = 31
ny = 31
nxc = nx-1
nyc = ny-1
nxd = nx+1
nyd = ny+1
re = 100 # レイノルズ数
r1 = 1./re
pr = 0.71 # プラントルズ数 (空気)
ar = 0.2 # Gr/Re^2
dt = 0.002 # 時間刻み
td = 1./dt
bx = 0.98 # 格子生成パラメータx
by = 0.98 # 格子生成パラメータy
ja = ny-5 # 入り口の格子 No.
jb = 5 # 出口の格子 No
km = 60 # SOR法の最大反復回数
const = 1.0 # SOR法の加速係数
eps = 0.0001 # 繰り返し演算打ち切り誤差
# --------- 配列初期化
a1=np.zeros(nx) # ∂/∂x
b1=np.zeros(nx) # ∂/∂x
c1=np.zeros(nx) # ∂/∂x
a2=np.zeros(nx) # ∂/∂x^2
b2=np.zeros(nx) # ∂/∂x^2
c2=np.zeros(nx) # ∂/∂x^2
a3=np.zeros(ny) # ∂/∂y
b3=np.zeros(ny) # ∂/∂y
c3=np.zeros(ny) # ∂/∂y
a4=np.zeros(ny) # ∂/∂y^2
b4=np.zeros(ny) # ∂/∂y^2
c4=np.zeros(ny) # ∂/∂y^2
psi=np.zeros((ny,nx)) # ψ
omg=np.zeros((ny,nx)) # ω
tmp=np.zeros((ny,nx)) # ωバックアップ
u=np.zeros((ny,nx)) # 流速 u
v=np.zeros((ny,nx)) # 流速 v
t=np.zeros((ny,nx)) # 温度 T
# -------------- 格子生成
xx=np.zeros(nx)
yy=np.zeros(ny)
x=np.zeros(nxd)
y=np.zeros(nyd)
# 不均等格子形成
fa=(np.exp(bx)+1.)/(np.exp(bx)-1.)
fb=(np.exp(by)+1.)/(np.exp(by)-1.)
# ----------- X
for i in range(nx):
bxa=bx*float(i)/float(nxc)
xq=fa*(np.exp(bxa)-1)/(np.exp(bxa)+1)
if xq<0:
xq=0.
if xq>1.:
xq=1.
x[i]=xq
x00=x[0]*2.-x[1]
x[nx]=x[nxc]*2.-x[nxc-1]
for i in range(nx):
xx[i]=x[i+1]
for i in range(nx): # 不均一格子座標差分情報 X
x1=x[i+1]-x[i]
if i==0:
x2=x[i]-x00
x3=x[i+1]-x00
x4=x[i+1]-x[i]*2.+x00
else:
x2=x[i]-x[i-1]
x3=x[i+1]-x[i-1]
x4=x[i+1]-x[i]*2.+x[i-1]
a1[i]=-x1/(x2*x3)
b1[i]=x4/(x1*x2)
c1[i]=x2/(x1*x3)
a2[i]=2./(x2*x3)
b2[i]=-2./(x1*x2)
c2[i]=2./(x1*x3)
# ----------- Y
for j in range(ny):
bya=by*float(j)/float(nyc)
yq=fb*(np.exp(bya)-1)/(np.exp(bya)+1)
if yq<0:
yq=0.
if yq>1.:
yq=1.
y[j]=yq
y00=y[0]*2.-y[1]
y[ny]=y[nyc]*2.-y[nyc-1]
for j in range(ny):
yy[j]=y[j+1]
for j in range(ny): # 不均一格子座標差分情報 Y
y1=y[j+1]-y[j]
if j==0:
y2=y[j]-y00
y3=y[j+1]-y00
y4=y[j+1]-y[j]*2.+y00
else:
y2=y[j]-y[j-1]
y3=y[j+1]-y[j-1]
y4=y[j+1]-2.*y[j]+y[j-1]
a3[j]=-y1/(y2*y3)
b3[j]=y4/(y1*y2)
c3[j]=y2/(y1*y3)
a4[j]=2./(y2*y3)
b4[j]=-2./(y1*y2)
c4[j]=2./(y1*y3)
X,Y =np.meshgrid(xx,yy) # 2次元データ表示用グリッド
#
# --- 初期条件
ps0 = y[nyc]-y[ja] # φ0 は ya から y までの u の積分 u=1.流入量
for i in range(nx):
psi[nyc][i]=ps0 # 上端の条件
for j in range(jb,ny):
psi[j][nxc]=ps0 # 出口の条件
#
# ----------- 計算ループ ----------------
#
lmax=3000 # 繰り返し計算回数
for l in range(1,lmax+1):
# STEP 1 境界条件
for j in range(ny): # 左右
omg[j][0]=(a2[0]*c1[0]/a1[0]-c2[0])*psi[j][1]
omx = (c2[nxc]*a1[nxc]/c1[nxc]-a2[nxc])*psi[j][nxc-1]
omx2= (c2[nxc]*b1[nxc]/c1[nxc]-b2[nxc])*ps0
omg[j][nxc]=omx+omx2
t[j][0]=t[j][1] # 左側面
t[j][nxc]=t[j][nxc-1] # 右側面
for j in range(ja+1,nyc): # 左側(出口より上)
omg[j][0]=0.
psi[j][0]=(y[j]-y[ja])/(y[nyc]-y[ja])*ps0
t[j][0]=.8 # 入温度
for j in range(jb): # 右側(入口より下)
omg[j][nxc]=omg[j][nxc-1]
psi[j][nxc]=(y[j]-y[0])/(y[jb]-y[0])*ps0
for i in range(nx): # 上下面
omg[0][i]=(a4[0]*c3[0]/a3[0]-c4[0])*psi[1][i]
t[0][i]=.4 # 下面温度
omy =(c4[nyc]*a3[nyc]/c3[nyc]-a4[nyc])*psi[nyc-1][i]
omy2=(c4[nyc]*b3[nyc]/c3[nyc]-b4[nyc])*ps0
omg[nyc][i]=omy+omy2
t[nyc][i]=0.1 # 上面温度
# STEP 2 ψの時間発展の計算 SOR法
for k in range(km):
for j in range(1,nyc):
for i in range(1,nxc):
pso=psi[j][i] # 前回のψ
tmp[j][i]=pso
psx = a2[i]*psi[j][i-1]+c2[i]*psi[j][i+1]
psy = a4[j]*psi[j-1][i]+c4[j]*psi[j+1][i]
pss = -(psx+psy+omg[j][i])/(b2[i]+b4[j]) # psi^* の計算
psi[j][i]=pso+const*(pss-pso)
err2=0.
for j in range(1,nyc): # 偏差のチェック
for i in range(1,nxc):
bb=np.absolute(psi[j][i]-tmp[j][i])
if bb>err2:
err2=bb
if err2<eps: # 偏差が規定値以下ならループから抜ける
break
# STEP 3 ωの時間発展の計算
for j in range(1,nyc):
for i in range(1,nxc):
omgo=omg[j][i]
psy = a3[j]*psi[j-1][i]+b3[j]*psi[j][i]+c3[j]*psi[j+1][i] # ∂ψ/∂y
omx = a1[i]*omg[j][i-1]+b1[i]*omgo+c1[i]*omg[j][i+1] # ∂ω/∂x
omy = a3[j]*omg[j-1][i]+b3[j]*omgo+c3[j]*omg[j+1][i] # ∂ω/∂y
psx = a1[i]*psi[j][i-1]+b1[i]*psi[j][i]+c1[i]*psi[j][i+1] # ∂ψ/∂x
omx2 = a2[i]*omg[j][i-1]+b2[i]*omgo+c2[i]*omg[j][i+1] # ∂^2ω/∂x^2
omy2 = a4[j]*omg[j-1][i]+b4[j]*omgo+c4[j]*omg[j+1][i] # ∂^2ω/∂y^2
tx = a1[i]*t[j][i-1]+b1[i]*t[j][i]+c1[i]*t[j][i+1] # ∂T/∂x
omg[j][i]=omgo+((omx2+omy2)*r1+tx*ar-psy*omx+psx*omy)*dt # ωの更新
# STEP 4 温度の時間発展の計算
for j in range(1,nyc):
for i in range(1,nxc):
u[j][i]= a3[j]*psi[j-1][i]+b3[j]*psi[j][i]+c3[j]*psi[j+1][i] # u= ∂ψ/∂y
v[j][i]=-(a1[i]*psi[j][i-1]+b1[i]*psi[j][i]+c1[i]*psi[j][i+1]) # v=-∂ψ/∂x
to = t[j][i]
tx = a1[i]*t[j][i-1]+b1[i]*to+c1[i]*t[j][i+1] # ∂T/∂x
ty = a3[j]*t[j][i-1]+b3[j]*to+c3[j]*t[j+1][i] # ∂T/∂y
tx2 = a2[i]*t[j][i-1]+b2[i]*to+c2[i]*t[j][i+1] # ∂^2T/∂x^2
ty2 = a4[j]*t[j-1][i]+b4[j]*to+c4[j]*t[j+1][i] # ∂^2T/∂y^2
t[j][i]=to+(-u[j][i]*tx-v[j][i]*ty+(tx2+ty2)*r1/pr)*dt # T の更新
# ------< 結果の表示 >-------------------
if l%500==0:
print("loop= ",l," Time= ",'{:.2f}'.format(l*dt)," k=",k," err2=",'{:.2e}'.format(err2))
fig=plt.figure(figsize=(7,7))
ax1 = fig.add_subplot(1, 1, 1)
ax1.set(xlabel='x',ylabel='y')
ax1.set_title('流れ & 温度')
ax1.contourf(X,Y,t,cmap='autumn_r')
ax1.quiver(X,Y,u,v,color='silver')
plt.show()
loop= 500 Time= 1.00 k= 0 err2= 3.27e-05
loop= 1000 Time= 2.00 k= 0 err2= 1.81e-05
loop= 1500 Time= 3.00 k= 0 err2= 1.03e-05
loop= 2000 Time= 4.00 k= 0 err2= 5.06e-06
loop= 2500 Time= 5.00 k= 0 err2= 1.99e-06
loop= 3000 Time= 6.00 k= 0 err2= 5.67e-07