「物理定理＆法則」カテゴリーアーカイブ

1.経緯

放送大学の「物理と化学のための数学演習」という授業のレポートの課題のひとつに「二重振り子」があったので、忘れないようにここにメモっておきます。

2.レポート課題

天井から長さ \(\ell\) の紐で吊るされた質量 \(M\) の錘に、もう一つの同じ長さ \(\ell\) の紐で同じ質量の錘が垂れ下がった、二重振り子の微小振動を考える。この問題は自由度２の連成振動となっている。以下の問いに答えよ。
\(\textbf{[1]}\) それぞれの紐が鉛直線となす角度を \(\theta_1\,,\,\theta_2\,\)とし、近似式、\(\sin\theta\simeq\theta\,\)を用いて、２つの錘の運動方程式を導き、この連成振動の基準座標と基準振動数を求めよ。紐の質量は小さいとして無視する。
\(\textbf{[2]}\) ２つの紐を変形しない同じ質量 \(m\) の棒で置き換えるとどうなるか。棒の重心はその真ん中にあるとする。

※　2. の問題は、私のやり方が拙かったせいか、解析解が得られませんでした。そこで、1. だけをここにメモります。

3.方程式の導出

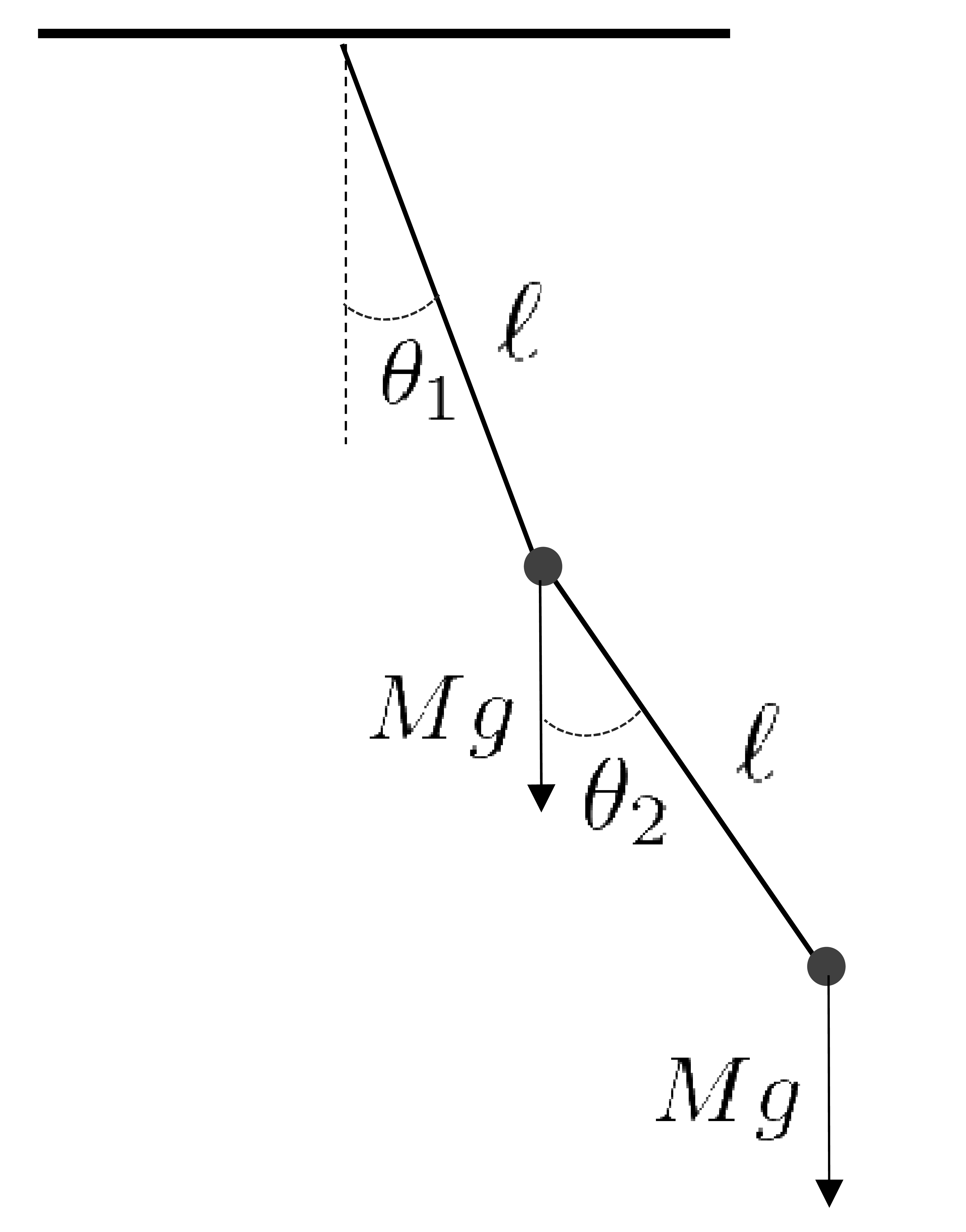最初のオモリの座標を \((x_1,y_1)\,\) , そこから垂れ下がったオモリの座標を \((x_2,y_2)\,\) とする。

\(x_1=\ell\sin\theta_1\qquad y_1=-\ell\cos\theta_1\)
\(x_2=x_1+\ell\sin\theta_2=\ell(\sin\theta_1+\sin\theta_2)\)
\(y_2=y_1-\ell\cos\theta_2=-\ell(\cos\theta_1+\cos\theta_2)\)
\(\dot{x}_1=\ell\cos\theta_1\dot{\theta}_1\simeq\ell\dot{\theta}_1\)
\(|\dot{x}_1|^2=\ell^2\dot{\theta}_1^2\)
\(\dfrac{1}{2}|\dot{x}_1|^2=\dfrac{\ell^2}{2}\dot{\theta}_1^2\)
\(\dot{x}_2=\ell(\cos\theta_1\dot{\theta}_1+\cos\theta_2\dot{\theta}_2)\simeq\ell(\dot{\theta}_1+\dot{\theta}_2)\)
\(\dfrac{1}{2}|\dot{x}_2|^2=\dfrac{\ell^2}{2}(\dot{\theta}_1+\dot{\theta}_2)^2\)

\(\theta_1\,,\,\theta_2\,\)が小さいとするので、運動エネルギーは \(\quad T=\dfrac{M\ell^2}{2}\dot{\theta}_1^2+\dfrac{M\ell^2}{2}(\dot{\theta}_1+\dot{\theta}_2)^2\)

ポテンシャル・エネルギーは\(\quad U=-Mg\ell(\cos\theta_1+\cos\theta_1+\cos\theta_2)\)

よって、ラグラジアン\(\,L\,\)は

\(L=T-U=\dfrac{M\ell^2}{2}(2\dot{\theta}_1^2+2\dot{\theta}_1\dot{\theta}_2+\dot{\theta}^2)+Mg\ell(2\cos\theta_1+\cos\theta_2)\)

\(\dfrac{\partial L}{\partial\theta_1}\,=-2Mg\ell\sin\theta_1\simeq -2Mg\ell\theta_1\hspace{12mm}\dfrac{\partial L}{\partial\dot{\theta}_1}=M\ell^2(2\dot{\theta}_1+\dot{\theta}_2)\)

\(\dfrac{\partial L}{\partial\theta_2}\,=-Mg\ell\sin\theta_2\simeq -Mg\ell\theta_2\hspace{16mm}\dfrac{\partial L}{\partial\dot{\theta}_2}=M\ell^2(\dot{\theta}_1+\dot{\theta}_2)\)

オイラー・ラグランジュ方程式は\(\quad\dfrac{d}{dt}\left(\dfrac{\partial L}{\partial\dot{q}_1}\right)=\dfrac{\partial L}{\partial q}\,\,\)なので

\(2\ddot{\theta}_1+\ddot{\theta}=-2\dfrac{g}{\ell}\theta_1\qquad \ddot{\theta}_1+\ddot{\theta}_2=-\dfrac{g}{\ell}\theta_2\quad\)の関係が得られる。
これより
\(\left(\begin{array}{@{\,}c@{\,}}\ddot{\theta}_1\\[2pt] \ddot{\theta}_2\end{array}\right)=\dfrac{g}{\ell}\left(\begin{array}{@{\,}rr@{\,}}-2&1\\[2pt]2&-2\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt] \theta_2\end{array}\right)\qquad\)の連立微分方程式が導かれる。
\(\hspace{28mm}\)行列\(\,\,K\,\)

4.方程式の解法

この行列 \(K\) を対角化することで、方程式を解く。まず \(K\) の固有値と固有ベクトルを求める。
固有値 \(\lambda\) は、固有ベクトル \(\textbf{x}\) と \(K\textbf{x}=\lambda\textbf{x}\) の関係にあるので、\(\det{(K-\lambda I)}=0\) より
\(\lambda^2+4\lambda+2=0\qquad \lambda=-2\pm\sqrt{2}\qquad\)が得られる。

\(\textbf{(4-1)} \,\,\lambda_1=-2+\sqrt{2}\) のとき

\(\quad(K-\lambda_1 I)=\left(\begin{array}{@{\,}rr@{\,}}-\sqrt{2}&1\\[2pt]2&-\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}x_1\\[2pt] x_2\end{array}\right)=0\qquad\) より

\(\quad x_1=\dfrac{1}{\sqrt{3}}\qquad x_2=\dfrac{\sqrt{2}}{\sqrt{3}}\qquad\quad \textbf{x}_1=\left(\begin{array}{@{\,}r@{\,}}\frac{1}{\sqrt{3}}\\[2pt]\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\)

\(\textbf{(4-2)} \,\,\lambda_2=-2-\sqrt{2}\) のとき

\(\quad(K-\lambda_2 I)=\left(\begin{array}{@{\,}rr@{\,}}\sqrt{2}&1\\[2pt]2&\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}x_1\\[2pt] x_2\end{array}\right)=0\qquad\) より

\(\quad x_1=\dfrac{1}{\sqrt{3}}\qquad x_2=-\dfrac{\sqrt{2}}{\sqrt{3}}\qquad\quad \textbf{x}_2=\left(\begin{array}{@{\,}r@{\,}}\frac{1}{\sqrt{3}}\\[2pt]-\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\)

5.正則行列の逆行列

固有ベクトルを縦に並べた行列 \(P\) を用いて \(P^{-1}KP\) として \(K\) を対角化する。

\(\quad P=\left(\begin{array}{@{\,}rr@{\,}}\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{3}}\\[3pt]\frac{\sqrt{2}}{\sqrt{3}}&-\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\qquad\quad P^{-1}=\left(\begin{array}{@{\,}rr@{\,}}\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{2\sqrt{2}}\\[3pt]\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2\sqrt{2}}\end{array}\right)\)

この \(P^{-1}\) を用いて、新しい変数 \(\Theta_1\,\,,\,\,\Theta_2\,\,\)を定義する。

\(\quad\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)=P^{-1}\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt]\theta_2\end{array}\right)=\left(\begin{array}{@{\,}rr@{\,}}\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{2\sqrt{2}}\\[3pt]\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2\sqrt{2}}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt]\theta_2\end{array}\right)\)

元の連立微分方程式は、変数　\(\Theta_1\,\,,\,\,\Theta_2$\,\,\)に対する以下の微分方程式と等価である。

\(\quad\dfrac{d}{dt}\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)=\dfrac{g}{\ell}\left(\begin{array}{@{\,}rr@{\,}}-2+\sqrt{2}&0\\[3pt]0&-2-\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)\)

最終的に、運動は２つの固有振動の足し合わせで表され、それぞれの固有振動数 \(\omega_1\,\,,\,\,\omega_2\,\,\)は、

\(\quad\omega_1=\sqrt{2+\sqrt{2}}\sqrt{\dfrac{g}{\ell}}\quad,\quad \omega_1=\sqrt{2-\sqrt{2}}\sqrt{\dfrac{g}{\ell}}\quad\) となる。

1-1. クラウジウスのビリアル定理

ビリアル定理は １９世紀に Clausius によって考案された。
「系の平均活力は、その（平均）ビリアル（の大きさ）に等しい。」
ここで登場する「活力」（”vis viva”）は、今日の運動エネルギーに相当します。 そもそも「活力」は古典力学の草創期にライプニッツが導入した量で、今日の運動エネルギーの２倍に相当する量 \(\,mv^2\,\)ですが、クラウジウスは \(\,mv^2/2\,\)とちょうど運動エネルギーと同じ量として用いています。ビリアル virial はラテン語のvis（「力」）からクラウジウスが作った造語です。ここでは、（力）×（位置ベクトル）をビリアルと呼ぶことにします。

距離の逆２乗則に従う重力やクーロン力の中心力で相互作用しあっている多体系では、長時間平均した運動エネルギー\(\,\langle\,T\,\rangle\,\)と平均の全ポテンシャルエネルギー\(\,\langle\,V\,\rangle\,\)は次の関係式を満たす。

\(\quad 2\langle\,T\,\rangle+\langle\,V\,\rangle=0\quad\cdots\,\)(1)

1-2. ビリアル定理の古典力学的証明

ここで位置ベクトル\(\,\vec{r}\,\)と運動量\(\,\vec{p}\,\)の内積の総和を以下のように考える。

\(\quad G=\displaystyle\sum_i\vec{p}_i\,\cdot\,\vec{r}_i\quad\cdot\,\)(2)

(2)式を時間\(\,t\,\)で微分する。

\(\quad\dfrac{dG}{dt}=\displaystyle\sum_i\vec{p}_i\cdot\dfrac{d\vec{r}_i}{dt}+\displaystyle\sum_i\dfrac{d\vec{p}_i}{dt}\cdot\vec{r}_i\)
\(\qquad\quad=\displaystyle\sum_i\,m_i(\vec{v}_i)^2+\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i\)
\(\qquad\quad=\displaystyle\sum_i2\times\dfrac{1}{2}m_i(\vec{v}_i)^2+\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i\)
\(\qquad\quad=2T+\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i\quad\cdots\,\)(3)

ここでは、次の関係式を使用している。

\(\quad \vec{p}_i=m_i\vec{v}_i\,,\qquad\vec{v}_i=\dfrac{d\vec{r}_i}{dt}\,,\qquad\vec{F}_i=\dfrac{d\vec{p}_i}{dt}\quad\cdots\,\)(4)

(3)式の両辺を\(\,0\,\)から時間\(\,t\,\)の範囲で積分して\(\,t\,\)で割り、\(t\to\infty\,\)の極限をとって長時間平均する。すると粒子が動き得る範囲は有限なので\(\,G\,\)も有限だから、左辺は\(\,0\,\)に収束する。

\(\quad\displaystyle\lim_{t\to\infty}\dfrac{1}{t}\displaystyle\int_0^t\dfrac{dG}{dt}=\displaystyle\lim_{t\to\infty}\dfrac{G(t)-G(0)}{t}=0\quad\cdots\,\)(5)

したがって、

\(\quad 0=2\langle\,T\,\rangle+\left\langle\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i\right\rangle\quad\cdots\,\)(6)

つまり、ビリアル定理を得る。

\(\quad\langle\,T\,\rangle=-\dfrac{1}{2}\left\langle\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i\right\rangle\quad\cdots\,\)(7)

次にポテンシャルエネルギー\(\,V\,\)が中心力ポテンシャルで、粒子間の距離に反比例する形で、系のポテンシャル\(\,V\,\)が各粒子対の相互作用の和によって書き表される場合、以下のように表される。

\(\quad V(r_1,\cdots,r_N)=\displaystyle\sum_{i\lt j}\dfrac{a_{ij}}{|\vec{r}_i-\vec{r}_j|}\quad\cdots\,\,\)(8)

粒子\(\,i\,\)に作用する力の合計\(\,\vec{F}_i\,\)は、ポテンシャルを位置座標で微分することで以下のように表すことが出来る。

\(\quad\vec{F}_i=-\nabla_{r_i}V=\displaystyle\sum_{j\ne i}\dfrac{a_{ij}(\vec{r}_i-\vec{r}_j)}{|\vec{r}_i-\vec{r}_j|^3}=\displaystyle\sum_{j\ne i}\vec{F}_{ij}\quad\cdots\,\)(9)

ここで、\(\,\vec{F}_{ij}\,\)は、粒子\(\,j\,\)から粒子\(\,i\,\)に働く力である。

\(\quad\vec{F}_{ij}=a_{ij}\dfrac{\vec{r}_i-\vec{r}_j}{|\vec{r}_i-\vec{r}_j|^3}\quad\cdots\,\)(10)

この\(\,\vec{F}_{ij}\,\)を用いると、ビリアル（力と位置ベクトルの内積）は次のように表せる。

\(\quad\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i=\displaystyle\sum_{i,j(i\lt j)}\vec{F}_{ij}\cdot\vec{r}_i+\displaystyle\sum_{i,j(j\lt i)}\vec{F}_{ij}\cdot\vec{r}_i\)
\(\qquad\qquad\quad=\displaystyle\sum_{i,j(i\lt j)}\vec{F}_{ij}\cdot\vec{r}_i+\displaystyle\sum_{i,j(i\lt j)}\vec{F}_{ji}\cdot\vec{r}_j\qquad\because\,i\leftrightarrow j\)
\(\qquad\qquad\quad=\displaystyle\sum_{i,j(i\lt j)}\vec{F}_{ij}\cdot(\vec{r}_i-\vec{r}_j)\quad\because\,\vec{F}_{ji}\!=\!-\vec{F}_{ij}\,\,\cdots\,\)(11)

(10)式を(11)式に代入すると

\(\quad\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i=\!\displaystyle\sum_{i,j(i\lt j)}\dfrac{a_{ij}}{|\vec{r}_i-\vec{r}_j|}\)
\(\qquad\qquad\qquad=\displaystyle\sum_{i,j(i\lt j)}\!V_{ij}=\!\displaystyle\!\sum_{i,j(i\lt j)}\!V_{ji}\quad\cdots\,\)(12)

よって(6)式は以下のように表すことが出来る。

\(\quad 0=2\langle\,T\,\rangle+\left\langle\displaystyle\sum_i\vec{F}_i\cdot\vec{r}_i\right\rangle=2\langle\,T\,\rangle+\left\langle\displaystyle\sum_{i,j(i\lt j)}V_{ij}\right\rangle\)
\(\qquad\qquad=2\langle\,T\,\rangle+\langle\,V\,\rangle\quad\cdots\,\)(13)

1. ミクロの世界の量子状態

1-1. 箱の中の粒子

一次元の粒子の波動方程式を考える。\(\,x\,\)軸上に、\(\,x=0\,\)から\(\,x=L\,\)までの長さが\(\,L\,\)の区間(\(\,0\ge\,x\ge\,L\,\))を考え、この区間の内部でだけ粒子が運動できるモノとする。このような状況の粒子を、1次元の箱の中の粒子と呼ぶ。
箱の外に出られないように、箱の外の位置エネルギーを\(\,\infty\,\)とする。また、箱の中では粒子に力が働かず自由に運動できるように、位置エネルギーを\(\,0\,\)とする。
解くべき方程式は、定常状態の波動方程式 \(\,\hat{H}\phi(x)=E\phi(x)\,\) であり、粒子の質量を\(\,m\,\)とするとハミルトニアン\(\,\hat{H}\,\)は以下のようになる。

\(\quad \hat{H}=-\dfrac{\hbar^2}{2m}\Delta+U(x)\quad\cdots\,\)(1.1)

変数は\(\,x\,\)のみの1次式なので、ラプラシアン\(\,\Delta\,\)は\(\,x\,\)の2次微分 \(\,d^2/dx^2\,\)に等しい。箱の外では位置エネルギーが無限大だから、\(\,\hat{H}\phi=E\phi\,\)が成り立つためには、\(\phi=0\,\)にならなければならない。
すなわち、箱の外の確率密度は\(\,0\,\)になり、粒子は箱の外には存在しない。次に箱の中では、位置エネルギーを\(\,U(x)=0\,\)としたので、波動方程式は次のような2次微分を含む方程式になる。

\(\quad -\dfrac{\hbar^2}{2m}\ \dfrac{d^2\phi}{dx^2}=E\phi\quad\cdots\,\)(1.2)

この式では\(\,\phi\,\)と\(\,x\,\)以外はすべて定数であり、次の形の基本的な微分方程式となっている

\(\quad \dfrac{d^2\phi}{dx^2}=-k^2\phi\quad\cdots\,\)(1.3)

ここで右辺の\(\,k\,\)は、求めるべきエネルギー\(\,E\,\)を含み、次式で与えられる定数である

\(\quad k=\left(\dfrac{2mE}{\hbar^2}\right)^{1/2}\quad\cdots\,\)(1.4)

式 (1.3)の一般解は指数関数または三角関数を含む次式の形に表される

\(\quad \phi(x)=ae^{ikx}+be^{-ikx}=A\sin kx+B\cos kx\quad\cdots\,\)(1.5)

波動関数の重要な性質として、連続性の条件があり、境界条件を考慮しなければならない。
箱の外では\(\,\phi=0\,\)であるから、箱の中(\(\,0\ge x\ge L\,)\)の\(\,\phi\,\)も箱の両端で値が\(\,0\,\)にならなくてはいけない。
そこで境界条件として \(\,\phi(0)=\phi(L)=0\,\) を使うと、\(\,x=0\,\)で\(\,\cos\,\)関数の部分は\(\,0\,\)にならないので、\(\sin\,\)の関数部分だけが残る。
また、\(\,x=L\,\)で\(\,\sin kx\,\)の値が\(\,0\,\)になるには \(\,kL=n\pi\,\)となり、その結果、波動関数とエネルギーがそれぞれ次のように決まる。

\(\quad\phi(x)=A\sin(n\pi x/L)\quad\cdots\,\)(1.6)

\(\quad E=\dfrac{(n\pi\hbar/L)^2}{2m}\quad\cdots\,\)(1.7)

ここで整数\(\,n\,\)は\(\,1,2,3\,\)などの自然数であり、これは量子数と呼ばれる。

(1.7) 式から、箱の中の粒子に許されるエネルギーは、図のように飛び飛びのエネルギー準位になる。

この結果は有限な空間に閉じ込められた粒子のエネルギーが飛び飛びになって量子化されることを示している。
ここで注目するべきことは、エネルギーが最低の基底状態、すなわち\(\,n=1\,\)の状態でも、エネルギーが\(\,0\,\)にならないことである。このエネルギーをゼロ点エネルギーという。

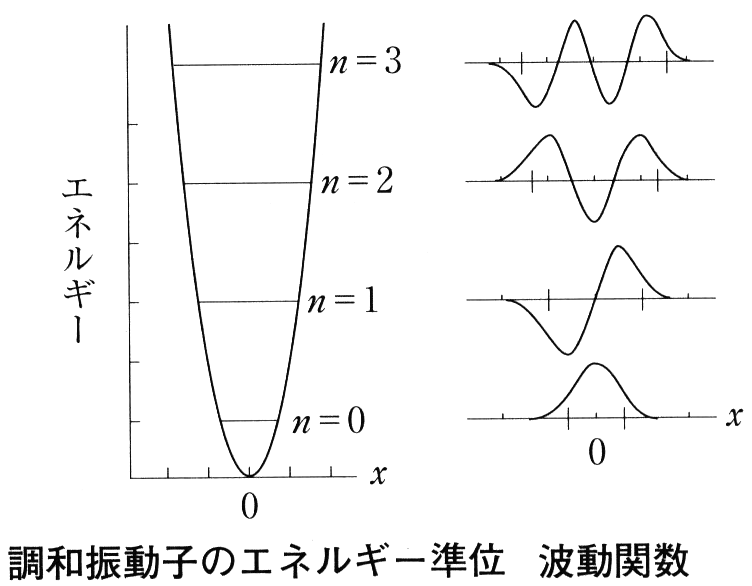(1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。

節になる位置は、\(\phi\,\)でも\(\,\phi^2\,\)も同じであり、図の右に示した\(\,\phi^2\,\)の図から明らかなように、節の位置に粒子が観測される確率は\(\,0\,\)である。

1-2. 調和振動子

波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。

この場合のハミルトニアンの運動エネルギーは箱の中の粒子の場合と同じになり、位置エネルギーは\(\,U(x)=\frac{1}{2}kx^2\,\) であるから、この調和振動子の波動方程式は次のように表される。

\(\left(-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2}+\dfrac{1}{2}kx^2\right)\Psi=E\Psi\quad\cdots\,\)(1.8)

この微分方程式は、次のように波動関数を仮定すると解くことができる。

\(\quad\Psi(x)=e^{-ax^2}\,\displaystyle\sum_{i=0}b_ix^i\quad\cdots\,\)(1.9)

解いた結果、次式に従うエネルギー準位が得られる。

\(\quad E_n=\left(n+\dfrac{1}{2}\right)h\nu\qquad(n=0,1,2,\cdots)\quad\cdots\,\)(1.10)

ここで、\(\,n=0,1,2,\cdots\,\) は振動の量子数(振動量子数)であり、\(h\,\)はプランク定数で、\(\nu\,\)はこの振動の固有振動数である。

調和振動子に許されるエネルギー準位は図の左に示すように等間隔になる。その間隔は、振動のエネルギー量子\(\,h\nu\,\)であり,固有振動数\(\,\nu\,\)はバネの力の定数が\(\,k\,\)で質量が\(\,m\,\)の古典力学の振動子と全く同じで、次式によって与えられる。

\(\quad\nu=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}\quad\cdots\,\)(1.11)

量子論の振動子には、古典力学と明らかに違った注目すべき特徴がある。エネルギーが最低の状態(基底状態)でも、そのエネルギーは\(\,0\,\)にならず、\(\,\dfrac{1}{2}h\nu\,\)というエネルギーをもって振動する。このエネルギーをゼロ点エネルギーといい、その時の振動をゼロ点振動という。

図の左に示したように、調和振動子の波動関数は中心の周りで振動子、遠くに行くと減衰する。値が\(\,0\,\)になる節の数は量子数\(\,n\,\)に等しく、エネルギーが高いほど多くなる。

1-3. 2粒子系の運動方程式

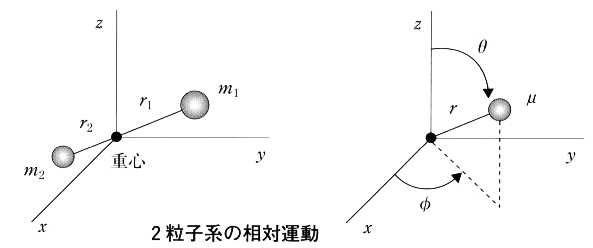2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。
ここで重心を座標原点に固定すると、\(\,r_1\,\)と\(\,r_2\,\)の和が\(\,r\,\)になり、2個の粒子の相対運動は長さが\(\,r\,\)の棒の先端につけた1つの球の運動の問題に単純化される。そのとき先端の粒子の質量\(\,\mu\,\)は、2個の粒子の質量の逆数の和の逆数になる。

\(\quad\)換算質量\(\quad\mu=\dfrac{1}{\frac{1}{m_1}+\frac{1}{m_2}}\)

こうして2個の粒子の相対運動は、換算質量をもつ1つの粒子の運動として取り扱うことが出来る。したがって、その波動方程式は次のように、1つの粒子の方程式と同じになる。

\(\quad\left(-\dfrac{\hbar^2}{2\mu}\Delta+U\right)\Psi=E\Psi\quad\cdots\,\)(1.13)

このような問題では、原点からの距離\(\,r\,\)が特別に重要なので、直交座標系\(\,(x,y,z)\,\)の代わりに、図の右に示す3次元の極座標\(\,(r,\theta,\varphi\,)\,\)を変数にとる。すると体積要素\(\,dxdydz\,\)とラプラシアン\(\,\Delta\,\)は、以下のように表される。

\(\quad\)体積要素\(\quad dxdydz=r^2\sin\theta dr d\theta d\varphi\quad\cdots\,\)(1.14)

\(\quad\)ラプラシアン\(\quad \Delta=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}\left(r^2\dfrac{\partial}{\partial r}\right)+\dfrac{1}{r^2}\Lambda\quad\cdots\,\)(1.15)

\(\quad\)ルジャンドリアン\(\quad \Lambda=\dfrac{1}{\sin\theta}\dfrac{\partial}{\partial\theta}\left(\sin\theta\dfrac{\partial}{\partial\theta}\right)+\dfrac{1}{\sin^2\theta}\dfrac{\partial^2}{\partial\varphi^2}\quad\)(1.16)

ここで、(1.15)式のラプラシアンに含まれる\(\,\Lambda\,\)は角度に依存する演算子であり、ルジャンドリアンと呼ばれる。

1-4. 剛体回転子

2量子系の波動方程式は、換算質量\(\,\mu\,\)を使うと原点から距離\(\,r\,\)のところに繋がれた1個の粒子の回転運動になる。距離\(\,r\,\)が一定なので\(\,r\,\)に関する微分は消えてしまい、また位置エネルギーも\(\,0\,\)とおいてよいので、その波動方程式は次のように単純な式になる。

\(\quad-\dfrac{\hbar^2}{2I}\Delta\Psi=E\Psi\quad\cdots\,\)(1.17)

ここで、次式で表される\(\,I\,\)は、重心を軸とする回転運動の慣性モーメントである。

\(\quad I=\mu r^2\quad\cdots\,\)(1.18)

(1.17)式の波動方程式は三角関数を組み合わせた式を仮定して解くことが出来、その結果、剛体回転子に許されるエネルギーは次式のように、整数値をとる回転量子数\(\,J\,\)によって飛び飛びの準位になる。

\(\quad E=\dfrac{J(J+1)\hbar^2}{2I}\qquad (J=0,1,2,\cdots)\quad\cdots\,\)(1.19)

剛体回転子の波動方程式は、数学でよく知られている球面調和関数\(\,Y_{J,m}(\theta,\varphi)\,\)というものになり、それは\(\,J\,\)のほかにもう一つの量子数\(\,m\,\)にも依存している。\(\,J\,\)が決まれば、それに従って\(\,m\,\)のとりうる範囲が決まる。\(\,m\,\)は\(\,J\,\)から\(\,J-1,J-2,\cdots,0,\cdots,-J\,\)まで、合計\(\,2J+1\,\)通りの値が可能である。

\(\quad Y_{00}(\theta,\varphi)=\left(\dfrac{1}{4\pi}\right)^{1/2}\quad\cdots\,\)(1.20)
\(\quad Y_{10}(\theta,\varphi)=\left(\dfrac{3}{4\pi}\right)^{1/2}\cos\theta\quad\cdots\,\)(1.21)
\(\quad Y_{1\pm1}(\theta,\varphi)=\mp\left(\dfrac{3}{8\pi}\right)^{1/2}\sin\theta\ e^{\pm i\varphi}\quad\cdots\,\)(1.22)
\(\quad Y_{20}(\theta,\varphi)=\left(\dfrac{5}{16\pi}\right)^{1/2}(3\cos^2\theta-1)(\quad\cdots\,\)(1.23)
\(\quad Y_{2\pm1}(\theta,\varphi)=\mp\left(\dfrac{15}{8\pi}\right)^{1/2}\sin\theta\ \cos\theta\ e^{\pm i\varphi}\quad\cdots\,\)(1.24)
\(\quad Y_{2\pm2}(\theta,\varphi)=\mp\left(\dfrac{15}{32\pi}\right)^{1/2}\sin^2\theta\ e^{\pm i2\varphi}\quad\)(1.25)

2.分子の回転

2-1. 回転運動のエネルギー

質量\(\,m\,\)、速度\(\,v\,\)の直線運動の大きさが運動量\(\,p=mv\,\)で、運動に伴うエネルギーは

\(\quad E=\dfrac{1}{2}mv^2=\dfrac{1}{2}\dfrac{p^2}{m}\quad\cdots\,\)(2.1)

である。一方、回転運動の大きさを表す量が角運動量であり、回転の軸から距離\(\,r\,\)にあって、運動量\(\,p\,\)で運動している物体の角運動量\(\,p_{\theta}\,\)は、

\(\quad p_{\theta}=r\times p\quad\cdots\,\)(2.2)

と表される。\(\,p_{\theta}\,\)は運動量を含むベクトルである。この角運動量を用いて、回転運動のエネルギーは

\(\quad E=\dfrac{1}{2}\dfrac{p_{\theta}^2}{I}\quad\cdots\,\)(2.3)

のように表される。式(2.1)と(2.3)を比較すると対応していることが分かる。

直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは

\(\quad I=\sum_im_ir_i^2=\sum_im_i(x_i^2+y_i^2+z_i^2)\quad\)(2.4)

であるが、2原子分子では換算質量\(\,\mu\,\)と原子間の距離\(\,r\,\)を使うと、以下の簡単な式で表すことが出来る

\(\quad \mu=\dfrac{m_1\cdot m_2}{m_1+m_2}\quad\cdots\,\)(2.5)

\(\quad I=\mu r^2\quad\cdots\,\)(2.6)

式(2.3)には運動量\(\,p_{\theta}\,\)が含まれており、この式を量子の世界にもちこむには、その\(\,p_{\theta}\,\)を演算子に置き換えればよい。その結果

\(\quad p_{\theta}=\sqrt{J(J+1)}\hbar\quad\cdots\,\)(2.7)

と置き換えることが出来る。従って、式(2.3)の2原子分子の場合の量子論的な表現は式(1.19)のように

\(\quad E=\dfrac{J(J+1)\hbar^2}{2I}=BJ(J+1)\qquad (J=0,1,2,\cdots)\quad\cdots\,\)(2.8)

となる。ここで\(\,J\,\)は回転量子数であり、\(\,0\,\)を含む整数のみが許される。すなわち回転エネルギーは量子化されており、飛び飛びの準位のみが許されることになる。\(\,B\,\)は回転定数と呼ばれるもので次式で表される。

\(\quad B=\dfrac{h}{8\pi^2I}\quad\)周波数単位}\(\qquad \dfrac{h}{8\pi^2c_0I}\quad\)波数単位\(\quad\cdots\,\)(2.9)

2-2. 観測される回転スペクトル

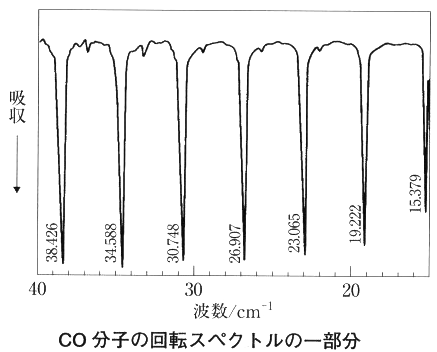回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。

回転量子数の\(\,J=0,1,2,3,\cdots\,\)に対して、エネルギー準位は\(\, 0,2B,6B,12B,\cdots\,\)となる。従って隣接するエネルギー準位間の大きさは \(\,2B,4B,6B,\cdots\,\)である。これを横軸にエネルギーをとってプロットすると図の下に示したようにスペクトルの位置が\(\,2B\,\)の間隔で並ぶ。これは実測のスペクトルとぴったり一致する。

このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。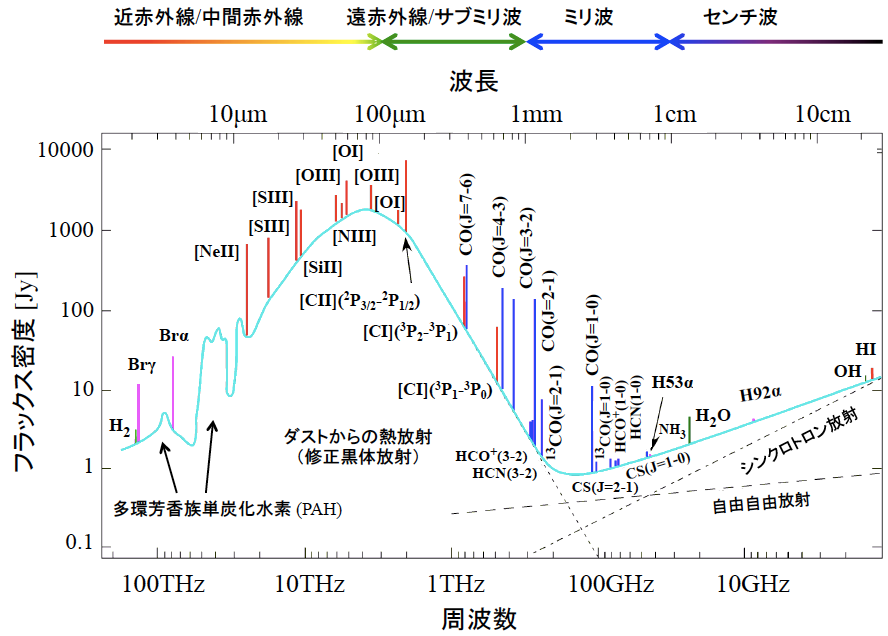

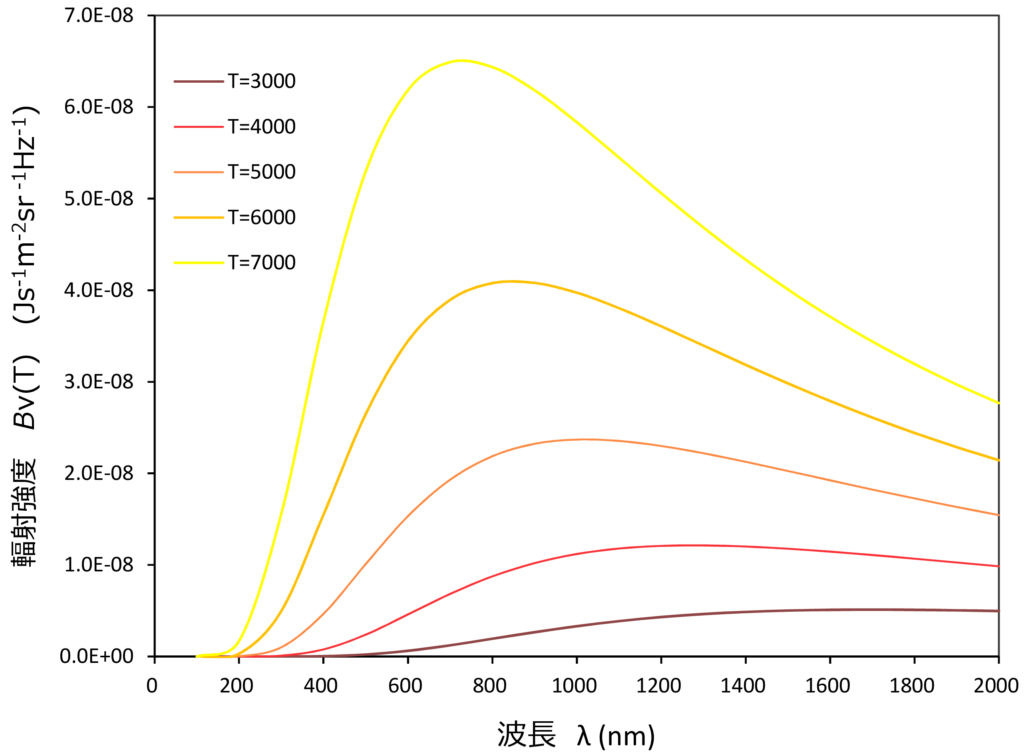
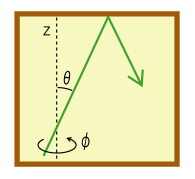
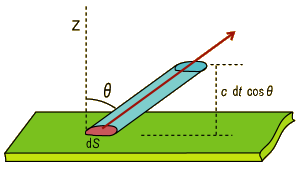以上のようにして、実測スペクトルの間隔から回転定数\(\,B\,\)が決定できる。この\(\,B\,\)は(2.9)式に定義された量であるから、\(\,B\,\)がわかるということは慣性モーメント\(\,I\,\)が実験的に求められたことを意味する。これより\(\,B\to I\to r\,\)のようにして、分子の構造を与える情報\(\,r\,\)が得られることになる。

2原子分子であるNO分子についても同様な解析が可能であり、実測スペクトルから分子構造に関する情報を導くことができる。それらの結果を以下の表にまとめる。

COの場合、\(J\!=\!1\!-\!0\,\)の回転遷移では、\(E=BJ(J+1)\,\) より、\(115.9\)GHz となり、\(^{13}\)COでは、\(110.8\)GHzとなる。\(J\!=\!2\!-\!1\,\)の場合は \(\,6B-2B=4B\,\)なので、\(^{12}\)CO は\(231.7\)GHzで、\(^{13}\)COは\(\,221.5\,\)GHzになる。

2-3. 観測されたスペクトル

爆発的星形成銀河（starburst銀河）M82の中心数100pc領域における、赤外線から電波に至る波長領域のスペクトル。大別して、(1)周波数に対して、連続的に放射強度が変化している「連続波放射」と、(2)ある特定の周波数でのみ、強い放射を示す「スペクトル線放射」とに分けられる。
連続波放射は、主に波長の長い電波域におけるシンクロトロン放射(磁場の中を高速で運動している電子からの放射)と、サブミリ波～赤外線域にかけて、大きな山をつくっている成分、すなわち、星間ダスト(星間空間中に存在する、シリケイトなどの固体微粒子)からの熱放射の重ね合わせとしてよく説明でできる。
この他、ミリ波付近には自由・自由遷移放射(電離領域中を運動する自由電子からの放射)も見られる。一方、この波長帯のスペクトル線放射としては、原子からの再結合線(桃色)・微細構造線(赤)・超微細構造線、分子からの回転線(青)などがみられる。

特殊相対論の質量とエネルギーの関係式を確認してみる

1．前準備

1-1. テイラー展開

閉区間 [\(\,a\,,\,b\,\)]で\(\,n\,\)回微分可能な関数\(\,f(x)\,\)において、\(n\to\infty\,\)にて

\(f(b)=f(a)\!+\!\dfrac{f'(a)}{1!}(b\!-\!a)\!+\!\dfrac{f”(a)}{2!}(b\!-\!a)^2\cdot\!+\!\dfrac{f^{(n)}(a)}{n!}(b\!-\!a)^n\,\)(1)

とできる。この (1)式を\(\,b=x\,\)とするのが別形である。
そして\(\,a=0\,\)とするのが　マクローリン展開( Maclaurin expansion )　である。

\(\quad f(x)=\displaystyle\sum_{n=0}^{\infty}\dfrac{f^{(n)}(0)}{n!}\,x^n\quad\cdots\,\)(2)

ここでは、ローレンツ変換で用いる関数\(\,\,f(x)=(1-x^2)^{-1/2}\,\,\)をマクローリン展開する。

1-2. \(\,\,f(x)\,\)の微分

\(\quad f(x)=\dfrac{1}{\sqrt{1-x^2}}=(1-x^2)^{-\frac{1}{2}}\quad\cdots\,\)(3)

を微分する。まず１回微分すると

\(\quad f'(x)=(-\dfrac{1}{2})(-2x)(1-x^2)^{-\frac{3}{2}}=x(1-x^2)^{-\frac{3}{2}}\quad\cdots\,\)(4)

２回微分では

\(\quad f^{\prime\prime}(x)=(1-x^2)^{-\frac{3}{2}}+(-\dfrac{3}{2})(-2x)x(1-x^2)^{-\frac{5}{2}}\)
\(\qquad=(1-x^2)^{\frac{3}{2}}+3x^2(1-x^2)^{-\frac{5}{2}}\quad\cdots\,\)(5)

さらに微分すると

\(\quad f^{\prime\prime\prime}(x)=(-\dfrac{3}{2})(-2x)(1-x^2)^{-\frac{5}{2}}+6x(1-x^2)^{-\frac{5}{2}}\)
\(\qquad +3x^2(-\dfrac{5}{2})(-2x)(1-x^2)^{-\frac{7}{2}}\)
\(\qquad =3x(1-x^2)^{-\frac{5}{2}}+6x(1-x^2)^{-\frac{5}{2}}+15x^3(1-x^2)^{-\frac{7}{2}}\)
\(\qquad =9x(1-x^2)^{-\frac{5}{2}}+15x^3(1-x^2)^{-\frac{7}{2}}\quad\cdots\,\)(6)

\(\quad f^{(4)}(x)=9(1-x^2)^{-\frac{5}{2}}+9x(-\dfrac{5}{2})(-2x)(1-x^2)^{-\frac{7}{2}}\)
\(\qquad+45x^2(1-x^2)^{-\frac{7}{2}}+15x^3(-\dfrac{7}{2})(-2x)(1-x^2)^{-\frac{9}{2}}\)
\(\qquad =9(1-x^2)^{-\frac{5}{2}}+90x^2(1-x^2)^{-\frac{7}{2}}+105x^4(1-x^2)^{-\frac{9}{2}}\quad\)(7)

\(\quad f^{(5)}(x)=225x(1-x^2)^{-\frac{7}{2}}+1050x^3(1-x^2)^{-\frac{9}{2}}\)
\(\qquad +945x^5(1-x^2)^{-\frac{11}{2}}\quad\cdots\,\)(8)

\(\quad f^{(6)}(x)=225(1-x^2)^{-\frac{7}{2}}+4725x^2(1-x^2)^{-\frac{9}{2}}\)
\(\qquad +7875x^4(1-x^2)^{-\frac{11}{2}}+10395x^6(1-x^2)^{-\frac{13}{2}}\quad\cdots\,\)(9)

1-3. \(\,\,f(x)\,\)のマクローリン展開

\(\quad f^{(n)}(x)\,\)に\(\,x=0\,\)を代入すると、

\(\quad f(0)=1\,,\quad f'(0)=0\,,\quad f^{\prime\prime}(0)=1\,,\quad f^{\prime\prime\prime}(0)=0\)
\(\quad f^{(4)}(0)=9\,,\quad f^{(5)}(0)=0\,,\quad f^{(6)}(0)=225\)

なので、それぞれの値を(2)式に代入すると

\(\quad f(x)=(1-x^2)^{-\frac{1}{2}}=1+\dfrac{1}{2}x^2+\dfrac{3}{8}x^4+\dfrac{5}{16}x^6+\cdots\,\,\)(10)

のように展開することが出来る

2．４次元時空での運動

2-1. 固有時間

慣性系\(\,S(t,x,y,z)\,\)と慣性系\(\,S'(t’,x’,y’,z’)\,\)において、
\(\quad dt=t’-t\,,\quad dx=x’-x\,,\quad dy=y’-y\,,\quad dz=z’-z\)

とすると、事象の隔たりを　世界距離( world distance :\(\,ds\,\) )といい、次の式で表される。

\(\quad ds^2=c^2dt^2-dx^2-dy^2-dz^2\quad\cdots\,\)(11)

ここで空間座標をまとめて\(\,\mathbf{x}\,\)で表すと

\(\quad ds^2=c^2dt^2-d\mathbf{x}^2\quad\cdots\,\)(12)

慣性系\(\,S’\,\)が\(\,S\,\)に対して、速度\(\,v\,\)で等速運動しているとすると、

ローレンツ変換 (Lorentz transformation )は

\(\quad\left(\begin{array}{c}\bf{x’}\\ct’\end{array}\right)=\gamma\left(\begin{array}{cc}1&\beta\\ \beta&1\end{array}\right)\left(\begin{array}{c}\bf{x}\\ct\end{array}\right)\quad\cdots\,\)(13)

ここで、\(\beta=\dfrac{v}{c}\,\)であり\(\quad \gamma=\dfrac{1}{\sqrt{1-\beta^2}}\,\)である。

この\(\,ds^2\,\)はローレンツ変換で不変である。

\(\quad ds^2=-c^2dt^2+d\mathbf{x}^2=-c^2dt’^2+d\mathbf{x}’^2\quad\cdots\,\)(14)

世界線の長さは\(\,\int\sqrt{-ds^2}\,\)として定義出来る。パラメータとして慣性系\(\,S\,\)の時間座標\(\,t\,\)そのものを選ぶことが出来る。

\(\quad\displaystyle\int\sqrt{-ds^2}=c\displaystyle\int dt\sqrt{1-\dfrac{1}{c^2}\left|\dfrac{d\mathbf{x}}{dt}\right|^2}=c\displaystyle\int d\tau\quad\cdots\,\)(15)

ここで時間定数\(\,\tau\,\)を定義する。固有時 (proper time )。

\(\quad d\tau=dt\sqrt{1-\dfrac{1}{c^2}\left|\dfrac{d\mathbf{x}}{dt}\right|^2}=dt’\sqrt{1-\dfrac{1}{c^2}\left|\dfrac{d\mathbf{x}’}{dt’}\right|^2}\quad\cdots\,\)(16)

式(15)は世界線に沿っての固有時間の長さを距離の単位で与える。これは、質点の軌道の形そのものによって定まる量なので、ローレンツ変換で不変である。

2-2. ４元速度

時間\(\,t\,\)を加えた４次元で固有時間に対する速度を考える。

\(\quad u_t=\dfrac{dct}{d\tau}\,,\,u_x=\dfrac{dx}{d\tau}\,,\,u_y=\dfrac{dy}{d\tau}\,,\,u_z=\dfrac{dz}{d\tau}\quad\cdots\,\)(17)

ここで、速度の大きさを考える場合、世界距離の計算と同様に時間成分の２乗はマイナスとなる。大きさを計算(内積をとる)する。

\(\quad-u_t^2+u_x^2+u_y^2+u_z^2=\dfrac{1}{d\tau^2}(-dct^2+dx^2+dy^2+dz^2)\)
\(\qquad =\dfrac{1}{d\tau^2}(-c^2d\tau^2)=-c^2\quad\cdots\,\)(18)

となり、４元速度の大きさは一定値になってしまう。
ここで、四元速度の表記を以下のようにする。

\(\quad u^{\mu}\equiv\dfrac{dx^{\mu}}{d\tau}\quad\cdots\,\)(19)

なお、\(u^0=u_t\,,\,u^1=u_x\,,\,u^2=u_y\,,\,u^3=u_z\,\)である。

式(16)、(17)より

\(\quad u^{\mu}=\dfrac{1}{\sqrt{1-\beta^2}}\dfrac{dx^{\mu}}{dt}=\dfrac{1}{\sqrt{1-\beta^2}}v^{\mu}\quad\cdots\,\)(20)

また、

\(\quad u^0=c\dfrac{dt}{d\tau}=\gamma\dfrac{cdt}{dt}=c\dfrac{1}{\sqrt{1-\beta^2}}\quad\cdots\,\)(21)

2-3. ４元運動量
４元速度を用いて４元運動量を\(\,m\,\)を静止質量として以下のように定義する。

\(\quad p^{\mu}=m\,u^{\mu}=m\gamma v^{\mu}\quad\cdots\,\)(22)

これにより、\(p^0\,\)は

\(\quad p^0=mu^0=mc\gamma=\dfrac{mc}{\sqrt{1-\beta^2}}\quad\cdots\,\)(23)

ここで、前準備の式(10)より

\(\quad\dfrac{1}{\sqrt{1-\beta^2}}=1+\dfrac{1}{2}\beta^2+\dfrac{3}{8}\beta^4+\dfrac{5}{16}\beta^6+\cdots\quad\cdots\,\)(24)

\(\,\beta=v/c\,\)なので、式(23)と(24)より

\(\quad p^0=mc+\dfrac{mc}{2}\dfrac{v^2}{c^2}+\dfrac{3mc}{8}\dfrac{v^4}{c^4}+\cdots\quad\cdots\,\)(25)

ここで、\(v/c\to 0\,\)の低速において、式(25)の両辺に光速\(\,c\,\)をかけると

\(\quad p^0c=mc^2+\dfrac{1}{2}mv^2+\cdots\qquad\cdots\,\)(26)

\(\,p^0c\,\)は質点のエネルギーを表しており、運動エネルギーと
静止エネルギー\(\,mc^2\,\)の和として表される。

1.プランクの法則 (Planck’s law)
物理学における黒体から輻射(放射)される電磁波の分光放射輝度、もしくはエネルギー密度の波長分布に関する公式。プランクの公式とも呼ばれる。ある温度\(\,T\,\)における黒体からの電磁輻射の分光放射輝度を全波長領域において正しく説明することができる。1900年、ドイツの物理学者マックス・プランクによって導かれた。

プランクはこの法則の導出を考える中で、輻射場の振動子のエネルギーが、あるエネルギー素量(現在ではエネルギー量子と呼ばれている)\(\,\epsilon=h\nu\,\)の整数倍になっていると仮定した。このエネルギーの量子仮説（量子化）はその後の量子力学の幕開けに大きな影響を与えている。
 プランクの放射式では、単位振動数\(\,\nu\,\)あたりの黒体輻射強度を以下のように表す。

\(\quad B_{\nu}(T)=\dfrac{2h}{c^2}\dfrac{\nu^3}{e^{h\nu/kT}-1}\quad\cdots\,\)(1)

なお、ここで\(\,c\,\)は光速、\(\,h\,\)はプランク定数、\(\,k\,\) はボルツマン定数である。このプランクの放射式に温度\(\,T\,\)に3000K\(\sim\)7000Kを代入してプロットしたのが下図である。

2.全黒体輻射強度 (Total blackbody radiation intensity)
このプランクの放射式を全振動数で積分したものを、全黒体輻射強度\(\,B(T)\,\) という。(1)式で、\(\,x=h\nu/kT\,\)とおくと、

\(\quad B_x(T)=\dfrac{2k^3T^3}{c^2h^2}\dfrac{x^3}{e^x-1}\quad\cdots\,\)(2)

となり、全振動数で積分すると

\(\quad \displaystyle\int_0^{\infty}B_{\nu}(T)d\nu=\displaystyle\int_0^{\infty}B_x(T)\,\dfrac{kT}{h}\,dx\quad\cdots\,\)(3)

\(\quad B(T)=\dfrac{2k^4T^4}{c^2h^3}\displaystyle\int_0^{\infty}\dfrac{x^3}{e^x-1}\,dx\quad\cdots\,\)(4)

(4)式の積分は\(\,\pi^4/15\,\)となるので、
全黒体輻射強度(放射輝度)[単位 Wm\(^{-2}\)sr\(^{-2}\)K\(^{-4}\)] は

\(\quad B(T)=\dfrac{2\pi^4k^4T^4}{15c^2h^3}=\dfrac{\sigma}{\pi}T^4\quad\cdots\,\)(5)
となる。

3.\(\,\,\,\,x^3/e^x-1\,\)の\(\,\,\)積分の計算

\(\quad\dfrac{x^3}{e^x-1}=\dfrac{x^3}{e^x}\dfrac{1}{1-e^{-x}}\quad\cdots\,\)(6)

(6)式の最後の項は公比\(\,e^{-x}\,\)の等比数列の和とすると

\(\quad\dfrac{1}{1-e^{-x}}=1+e^{-x}+e^{-2x}+\cdots\)
となるので

\(\quad\dfrac{x^3}{e^x-1}=x^3(e^{-x}+e^{-2x}+e^{-3x}+\cdots)\quad\cdots\,\)(7)

ここで\(\,x^pe^{-ax}\,\)の形の関数を積分するために、ガンマ関数を利用する。
ガンマ関数の定義から

\(\quad\varGamma(q)=\displaystyle\int_0^{\infty}y^{q-1}e^{-y}dy=(q-1)\,!\quad\cdots\,\)(8)

ここで、\(\,p=q-1\,\)とすると
\(\quad p\,!=\displaystyle\int_0^{\infty}y^pe^{-y}dy\quad\cdots\,\)(9)

\(\,\,y=ax\,\)とすると\(\,dy=a\,dx\,\)で、(9)式に代入すると

\(\quad p\,!=\displaystyle\int_0^{\infty}(ax)^pae^{-ax}dx=a^{p+1}\displaystyle\int_0^{\infty}x^pe^{-ax}dx\quad\cdots\,\)(10)

よって

\(\quad\displaystyle\int_0^{\infty}x^pe^{-ax}dx=\dfrac{p\,!}{a^{p+1}}\quad\cdots\,\)(11)

これを使って(7)式を積分すると

\(\quad\displaystyle\int_0^{\infty}\!\dfrac{x^3}{e^x-1}dx=\displaystyle\int_0^{\infty}\!x^3(e^{-x}+e^{-2x}+\cdots)dx=\dfrac{3!}{1^4}+\dfrac{3!}{2^4}+\cdots\quad\)

ここでゼータ関数より

\(\quad\zeta(4)=\displaystyle\sum_{n=1}^{\infty}\dfrac{1}{n^4}=\dfrac{1}{1^4}+\dfrac{1}{2^4}+\cdots=\dfrac{\pi^4}{90}\quad\cdots\,\)(12)

なので

\(\quad\displaystyle\int_0^{\infty}\dfrac{x^3}{e^x-1}dx=\dfrac{3!}{1^4}+\dfrac{3!}{2^4}+\cdots=3\,!\,\zeta(4)=\dfrac{\pi^4}{15}\quad\cdots\,\)(13)

4.放射エネルギー
全立体角に対する積分は
\(\quad\displaystyle\int\cos\theta\,d\Omega=\displaystyle\int_0^{2\pi}\displaystyle\int_0^{\frac{\pi}{2}}\cos\theta\,\sin\theta\,d\theta\,d\phi=\pi\quad\cdots\,\)(14)

よって黒体の単位面積当たりの放射エネルギー\(\,I\,\)は

\(\quad I=\pi\displaystyle\int B_{\nu}d\nu=\dfrac{2\pi^5k^4}{15c^2h^3}T^4=\sigma T^4\quad\cdots\,\)(15)

ここで、\(\,\sigma\,\)はステファン・ボルツマン係数である

\(\quad\sigma=\dfrac{2\pi^5k^4}{15c^2h^3}=5.67\times 10^{-8}\)W/m\(^2\)K\(^4\quad\cdots\,\)(16)

1. あらゆる物体は光を放っている
 電磁波というのは電荷を持った粒子が振動することで発生する。そして電荷を持った粒子は、どこからか飛んできた電磁波を受けると、その影響で振動する。そこらじゅうにある原子は内部に電荷を持っているのだから、何らかの方法で電磁波を放出し、また受け止めていると考えられる。

例えば太陽の光だって電磁波の一種だが、それを受け止めた物体は熱くなる。電磁波の形で遠くから届いたエネルギーが熱に変わるからだ。逆のことも起きている。キャンプファイヤーが終わった後で火を消すと辺りは真っ暗になるが、その真っ暗闇の中で、さっきまで焼かれていた石がぼんやりと赤黒く光っていることがある。そこらにある普通の石が、内部から光を放っているように見えて、少し不気味ではあるが、何だか綺麗だ。

他にも色んな例がある。ストーブの中で焼けた鉄板が赤く光っている。焚き火のときに炭が赤く光っている。ハロゲンヒーターが赤熱している。その光を浴びると、すぐに暖かく感じる。これは間にある空気を伝わって暖められるわけではない。光によって直接暖められるせいだ。このように、熱せられた物体から光や電磁波が出る現象を「熱放射」と呼ぶ。

では物体は何度くらいから光を出し始めるのだろう。実は目に見えないだけで、低い温度の物体でも電磁波を出しているらしい。体温の高い人が近くに来ると直接触らなくても暖かさを感じることがあるだろう。それはその人の体から、可視光線よりも低いエネルギーの光である赤外線が放射されているのだ。

2. ステファン・ボルツマンの法則
では物体は一体どれほどのエネルギーを熱放射の形で放出しているのだろうか？それを調べたのはヨーゼフ・ステファンという 19 世紀の科学者であり、実はあのボルツマンの師である。彼は他の学者たちが過去に行った幾つかの実験結果をまとめた上で、自らも白金の針金に電流を流して赤熱させる実験を行ったりして、熱放射のエネルギー\(\,K\,\)と物体の温度\(\,T\,\)との間に次のような関係があるのではないかという提案を行った。 (1879)

\(\quad K=\sigma T^4\quad\cdots\,\)(1)

この式は「ステファン・ボルツマンの法則」と呼ばれている。なぜボルツマンの名前が入っているかというと、後に、弟子のボルツマンが、当時の最新理論である電磁気学と熱力学を使って、この法則の根拠を説明することに成功したからである。 (1884)

にもかかわらず、この結果はしばらくの間認められることはなかった。多くの科学者がこの実験結果を確認しようとしたが、追試がうまくいかなかったのである。今ではその理由ははっきり分かっているのだが、この法則には少しばかり適用条件があって、当時はそのことがまだ良く分かっていなかったのである。ステファンの実験がうまく行ったのは偶然の幸運であろうと言われている。

3. 理論的導出
 電磁波はエネルギーだけでなく運動量をも持つのだということを、電磁気学で学んだ。そこで、こんなことを考えてみよう。容器の壁が温度\(\,T\,\)の物質で出来ていて、そこから放出された電磁波で容器の中が一様に満たされており、そのエネルギー密度が\(\,u\,\)になっていたとする。

 この仮定は次のような考えを根拠にしている。もし容器の壁から内側へ向けて電磁波が放出される一方だとすると、容器内部の電磁場のエネルギーは無限に増える一方となるだろう。しかしそうならないのは、容器の壁は電磁場を放出すると同時に吸収も行っていて、一定の状態で安定しているせいだと考えられる。容器の中の電磁場と容器の壁とは熱平衡に達しているというわけだ。電磁場に対しても、温度という概念が使えるということでもある。というわけで、\(\,u\,\)は\(\,T\,\)の関数だと言えるだろう。
さて、そのときの運動量密度\(\,w\,\)と\(\,u\,\)の間には\(\,u=cw\,\)という関係がある。

4. 電磁波のエネルギー密度
 マックスウェルの方程式から次の波動方程式が導かれる
\(\quad\nabla^2\mathbf{B}-\dfrac{1}{c^2}\dfrac{\partial^2\mathbf{B}}{\partial t^2}=0\qquad\nabla^2\mathbf{E}-\dfrac{1}{c^2}\dfrac{\partial^2\mathbf{E}}{\partial t^2}=0\quad\cdots\,\)(2)

空間に領域Dをとり、その内部で電磁場が荷電粒子系に及ぼす単位体積当たりの力は
\(\quad\mathbf{f}=\rho\mathbf{E}+\mathbf{j}\times\mathbf{B}\quad\cdots\,\)(3)
であるので荷電粒子系の運動方程式は
\(\quad\dfrac{d\mathbf{P}_{\text{粒子}}}{dt}=\displaystyle\int_{\mathrm{D}}\mathbf{f}\,dv\quad\cdots\,\)(4)
となる。\(\mathbf{P}_{\text{粒子}}\,\)は粒子系の全運動量である。

ここで電場についてのガウスの法則と拡張されたアンペールの法則を使って\(\,\mathbf{f}\,\)を表すと
\(\mathbf{f}=\epsilon_0(\nabla\cdot\mathbf{E})\mathbf{E}-\epsilon_0\dfrac{\partial\mathbf{E}}{\partial t}\times\mathbf{B}+\dfrac{1}{\mu_0}(\nabla\times\mathbf{B})\times\mathbf{B}\quad\cdots\,\)(5)

これよりD内の電磁場の運動量は単位体積当たり以下の値を持つ
\(\quad\mathbf{p}_{\text{場}}\equiv\epsilon_0\mathbf{E}\times\mathbf{B}\quad\cdots\,\)(6)

ここで電束密度\(\,\mathbf{D}=\epsilon_0\mathbf{E}\)、磁束密度\(\,\mathbf{B}=\mu_0\mathbf{H}\,\)であり、真空中を伝搬する電磁場の電場\(\,\mathbf{E}\)と磁束密度\(\,\mathbf{B}\)の大きさの間には\(\,|\mathbf{E}|=c|\mathbf{B}|\)なる関係が成立する。

電場の大きさを\(\,E=|\mathbf{E}|\)とすると電磁場のエネルギー密度は
\(\quad u=\dfrac{1}{2}(\mathbf{E}\cdot\mathbf{D}+\mathbf{B}\cdot\mathbf{H})=\dfrac{1}{2}\left(\epsilon_0E^2+\dfrac{E^2}{c^2\mu_0}\right)\)
\(\qquad =\dfrac{1}{2}(\epsilon_0E^2+\epsilon_0E^2)=\epsilon_0E^2\quad\cdots\,\)(7)

一方、運動量密度\(\,w\,\)は
\(\quad w=|\mathbf{D}\times\mathbf{B}|=\epsilon_0E\cdot\dfrac{E}{c}=\dfrac{\epsilon_0E}{c}=\dfrac{u}{c}\quad\cdots\,\)(8)

5. 電磁波による圧力

 ここで、容器の内部の電磁波を考える。電磁波は容器の壁に当たるたびに壁に運動量を与えるのだから、容器の壁を圧力\(\,p\,\)で押すことだろう。まずは、その\(\,p\,\)と\(\,u\,\)の関係を導く。

説明が簡単に済むように、一辺の長さが\(\,L\,\)の立方体の容器を考えてみる。そしてどの壁を考えても同じことではあるのだが、極座標の積分計算を分かりやすくする都合で、\(\,z\,\)軸の正の方向にある壁に与える圧力を考える。

容器内の全ての電磁波が一つの方向を向いているとする。その全運動量\(\,P\,\)は運動量密度\(\,w\,\)と体積\(\,V=L^3\,\)を掛けて、\(P=wL^3\,\)と表せる。

全ての電磁波の向かう一つの方向というのが、\(\,z\,\)軸に対して\(\,\theta\,\)の角度を持った方向だとすると、壁に当たって反射するたびに、合計で\(\,2P\cos\theta\,\)の運動量を与えることになる。

その頻度であるが、電磁波の速度の\(\,z\,\)軸方向成分が\(\,c\,\cos\theta\,\)であり、往復\(\,2L\,\)の距離を進むたびに再び同じ壁に当たるのだから、1秒間に\(\,c\,\cos\theta/2L\,\)回の衝突を行うことになる。

力というのは1 秒あたりの運動量変化のことであり、それを面積\(\,L^2\,\)で割れば圧力\(\,p\,\)が求まることになる。

\(\quad p=2P\cos\theta\times\dfrac{c\,\cos\theta}{2L}\div L^2\)
\(\qquad =2wL^3\cos\theta\times\dfrac{c\cos\theta}{2L^3}\)
\(\qquad =wc\,\cos^2\theta=u\,\cos^2\theta\quad\cdots\,\)(9)

という形になる。しかしこの結果は、全ての電磁波が一つの方向を向いていると仮定した上での話であり、実際にはあらゆる方向を向いているはずだから、全方向について平等に平均をしてやらないといけないだろう。その為には立体角の考えを使えば良さそうだ。自分が半径1の球の中心にいて、周囲をぐるっと見回していると想像してみよう。どの方向も等しいのだから、この球の表面積にわたって今の結果を積分してやればいい。平均を取るためにはそれを表面積\(\,4\pi\,\)で割ってやればいい。

\(\quad p=\dfrac{u}{4\pi}\displaystyle\int_0^{\pi}\cos^2\theta\sin\theta\,d\theta\displaystyle\int_0^{2\pi}d\phi\)
\(\qquad =\dfrac{u}{4\pi}\left[-\dfrac{1}{3}\cos^3\theta\right]_0^{\pi}\times 2\pi\)
\(\qquad =\dfrac{u}{3}\quad\cdots\)(10)

6. 熱力学的考察
 可逆過程での内部エネルギー(\(\,U\,\))変化において以下の関係式がある。
\(\quad dU=T\,dS-p\,dV\quad\) これを変形して
\(\quad\left(\dfrac{\partial U}{\partial V}\right)_T=T\left(\dfrac{\partial p}{\partial T}\right)_V-p\quad\cdots\,\)(11)

という式を作ることが出来る。これに\(\,T\,\)一定の条件下で\(\,V\,\)を変化させ、マクスウェルの関係式を当てはめる。電磁波の場合、この左辺はエネルギー密度\(\,u\,\)になる。

圧力\(\,p\,\)に式(10)を代入すると式(11)は
\(\quad u=\dfrac{1}{3}\,T\,\dfrac{du}{dT}-\dfrac{u}{3}\\[4pt]\therefore\,4u=T\,\dfrac{du}{dT}\qquad\dfrac{du}{u}=4\,\dfrac{dT}{T}\\[4pt]\quad\log u=4\log T+C\qquad\therefore\,\,u=aT^4\quad\cdots\text{(12)}\)となり、形の上ではステファン・ボルツマンの法則と同じものが導かれたことになる。

しかし\(\,u\,\)というのは、物体と電磁場とが熱平衡にあるときの電磁場のエネルギー密度を示しているのであって、物体から放出されるエネルギー\(\,K\,\)とは少し違う概念である。

7. 概念の整理
\(\,K\,\)の意味を「物体の単位表面積から単位時間あたりに放出されるエネルギー」だと言えるようにまとめることが出来れば使いやすい法則になりそうである。
微小面積\(\,dS\,\)から放出される電磁波をイメージする。
その微小面の法線方向から\(\,\theta\,\)だけずれた方向へ向かって微小時間\(\,dt\,\)に出て行った電磁波は、図のような筒状体積の内部にあることになるだろう。その体積は\(\,c\,\cos\theta\,dtdS\,\)である。

しかしこの筒状体積とエネルギー密度\(\,u\,\)をかけるだけで、そのエネルギー量が求まるほど単純ではない。なぜなら、このエネルギー密度\(\,u\,\)というのは、あらゆる方向に向かう電磁波が均等に重なり合った合計のエネルギー密度を表しているからである。

今知りたいのは、\(\,\theta\,\)方向へ流れる電磁波のエネルギーだけなのだが、その割合は全方向に向かう電磁波のエネルギーの中でどれくらいあると言えるだろうか。いや、厳密に\(\,\theta\,\)方向に向かう電磁波だけに限定してしまうとそれは無に等しいのである。だからある程度の微小幅を許容して考えないといけない。

こういう時は立体角の考えを使う。半径1の球殻を考え、その表面積の比で表すのである。角度\(\,d\theta\,\)と\(\,d\phi\,\)によって張られる球殻上の微小表面積は\(\,sin\theta\,d\theta\,d\phi\,\)と表されるから、全球殻の面積\(\,4\pi\,\)と比べた割合は\(\,1/4\pi\,\sin\theta\,d\theta\,d\phi\,\)となるだろう。

先ほど考えた筒状領域を、厳密に一方向として考えるのではなく、角度\(\,d\theta\,\)と\(\,d\phi\,\)の微小角度の幅を許してやれば、その範囲を向いている電磁波のエネルギーは

\(\quad\dfrac{1}{4\pi}uc\,\cos\theta\sin\theta\,d\theta\,d\phi\,dt\,dS\quad\cdots\,\)(13)

と表せることになる。この式(13)を微小面より上にある全ての方向について積分してやれば、微小面\(\,dS\,\)から微小時間\(\,dt\,\)内にあらゆる方向へ出て行くエネルギーを表せる。

\(\quad\dfrac{1}{4\pi}uc\,dt\,dS\displaystyle\int_0^{\pi/2}\cos\theta\sin\theta\,d\theta\displaystyle\int_0^{2\pi}d\phi\\[3pt]\qquad=\dfrac{1}{2}uc\,dt\,dS\displaystyle\int_0^{\pi/2}\dfrac{1}{2}\sin 2\theta\,d\theta\\[3pt]\quad =\dfrac{1}{2}uc\,dt\,dS\left[-\dfrac{1}{4}\cos 2\theta\right]_0^{\pi/2}\\[3pt]\quad =\dfrac{1}{4}uc\,dt\,dS\quad\cdots\,\text{(14)}\)

意味を考えれば今計算したのは\(\,K\,dt\,dS\,\)のことでもある。つまり\(\,K\,\)というのは、

\(\quad K=\dfrac{c}{4}u\quad\cdots\,\)(15)
に相当することが言えるのである。ここに先ほどの\(\,u=aT^4\,\)を代入すれば、

\(\quad K=\dfrac{ca}{4}\,T^4=\,\sigma T^4\quad\cdots\,\)(16)

という形が成り立っていることが言えるのである。普通はステファン・ボルツマンの法則と言えば、ここで使ったような意味での\(\,K\,\)と温度\(\,T\,\)の関係のことであり、「ステファン・ボルツマンの定数」として良く知られた\(\,\sigma\,\)もその意味に合うような数値が書かれていることが多い。

エネルギー保存の法則から振り子の周期 \(T\) の式を求める。
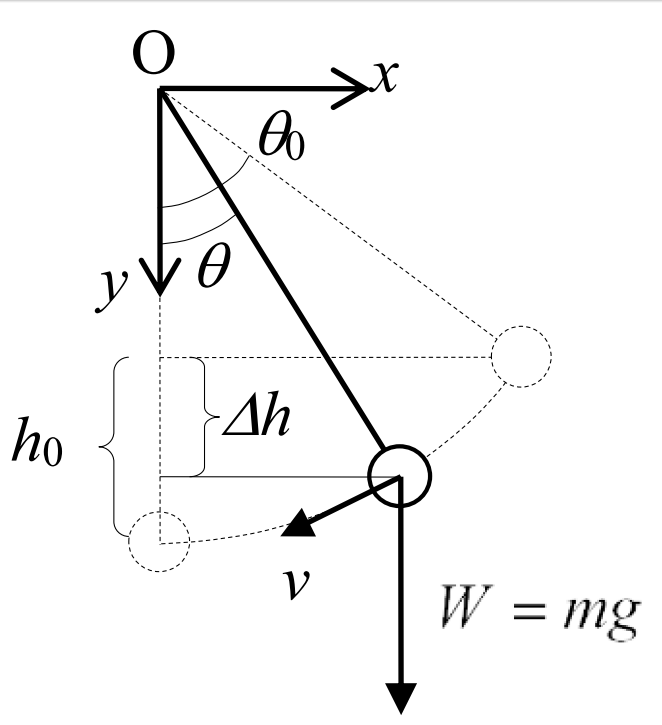振り子の支点より水平方向に \(\ x\ \)軸をとり、鉛直方向に \(\ y\ \)軸をとると、エネルギー保存則から、次式が成立する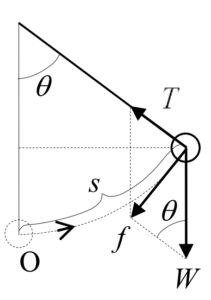

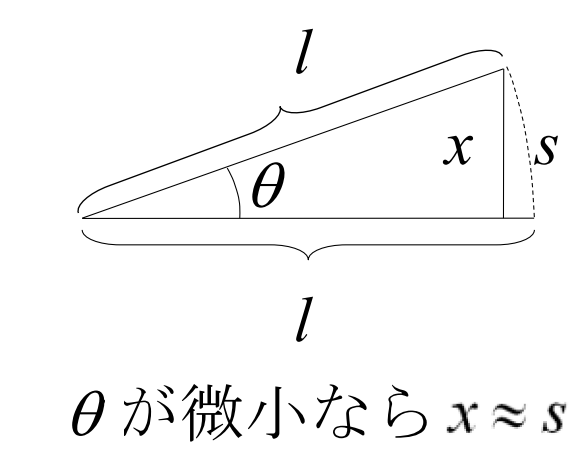\( \dfrac{1}{2}mv^2=mg\Delta h\quad\) (21)

ここで、\(\ v\ \)は重りが円周方向に移動する速度で、\(\Delta h\ \)は重りの落下距離である。ここで

\(\Delta h=l\cos\theta-l\cos\theta_0=l\ (\cos\theta-\cos\theta_0)\quad\) (22)
なので

\( \dfrac{1}{2}mv^2=mgl(\cos\theta-\cos\theta_0)\)
\( \therefore \ v=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\) (23)

さらに

\( v=\dfrac{ds}{dt}=l\dfrac{d\theta}{dt}\quad\) (24)

なので、以下の式が得られる。

\( l\dfrac{d\theta}{dt}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\)(25)

\( dt=\dfrac{1}{\sqrt{2}\omega}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (26)

\(\quad\because\,\,\omega:=\sqrt{\dfrac{g}{l}}\)

この(26)式を積分すると周期を求めることが出来る。積分範囲を4分の1周に相当する \(\ t=T/4\ \)とすると、右辺の積分範囲は\(\ \theta=0\sim\theta_0\ \)となるので、

\( \displaystyle\int_0^{\frac{T}{4}}dt=\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (27)

\(\therefore\,\, T=4\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (28)

この積分を行うために、半角公式を使って以下の変換を行う

\( \cos\theta=1-2\sin^2\frac{\theta}{2}\quad\cos\theta_0=1-2\sin^2\frac{\theta_0}{2}\)

ここで \(\,\,k:=\sin\frac{\theta_0}{2}\quad \sin\phi:=\sin\frac{\theta}{2}/k\,\,\)とすると

\( \cos\theta-\cos\theta_0=1-2\sin^2\frac{\theta}{2}-\left(1-2\sin^2\frac{\theta_0}{2}\right)\)

\(\quad=2\left(\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}\right)=2k^2\cos^2\phi\,\,\)となる

\(k\sin\phi=\sin\frac{\theta}{2}\,\,\)を両辺微分して\(\,\,k\cos\phi\,d\phi=\frac{1}{2}\cos\frac{\theta}{2}\,d\theta\)

\(d\theta=\dfrac{2k\cos\phi\,d\phi}{\cos\frac{\theta}{2}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-\sin^2\frac{\theta}{2}}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\)

なので

\(\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}=\dfrac{1}{\sqrt{2}k\cos\phi}\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\)

\(\quad=\dfrac{\sqrt{2}\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\,\,\)となり、第１種楕円積分の形になる。

［１］運動方程式

振り子には、図のような力が働く。ここで 重力は\( \ W=mg\ \)で糸の張力は\(\ \ T=W\cos\theta\ \) である。

\(W\ \)と\(\ T\ \)の合力\(\ f\ \)の向きは図のように半径\(\ l\ \)の円周の接線方向となり、その大きさは

\(f=W\sin\theta=mg\sin\theta\)　(1)

である。この合力\(\ f\ \)により、重りは円弧を描くように往復運動をする。ここで、運動を円軌道として考えるために、振り子の釣り合いの位置 O から、円弧に沿って\(\ s\ \)軸をとる。この合力\(\ f\ \)は重りを\(\ s\ \)軸の負の方向に運動させる力となるため、重りの運動方程式は

\( m\dfrac{d^2s}{dt^2}=-f=-mg\sin\theta\ \)　(2)

すなわち

\( \dfrac{d^2s}{dt^2}=-g\sin\theta\ \)　(3)

と表すことが出来る。　円弧の長さは \(\ s=l\ \theta\ \)で表せられ、２回微分は

\(\ \dfrac{d^2s}{dt^2}=l\dfrac{d^2\theta}{dt^2}\ \)　(4)

となるので、運動方程式は重りの角度\(\ \theta\ \)に対して

\( \dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\sin\theta\ \)　(5)

と表すことが出来る。

［２］運動方程式の近似解

　(5)式の運動方程式は、三角関数を含んでいるため、このままでは階を求めることが難しい。但し、円弧の角度\(\ \theta\ \)が微少の場合、三角形の高さ\(\ x=\sin\theta\ \)は円弧の長さ\(\ s\ \)にほぼ等しくなり
\(\quad x\ \approx\ s\ \)とおけるため

\( \sin\theta=\dfrac{x}{l}\ \approx\ \dfrac{s}{l}=\dfrac{l\theta}{l}=\theta\ \)　(6)

となり、運動方程式は

\( \dfrac{d^2\theta}{dt^2}=-\omega^2\theta\qquad \omega:=\sqrt{\dfrac{g}{l}}\quad\) (7)

と表すことが出来る。これは単振動で良く近似出来る。一般解は

\( \theta=A\sin\omega t+B\cos\omega t \)　(8)

ここで、 \( t=0\ \)で\(\ \theta=\theta_0\ \)として、(8)式に代入すると

\( \theta_0=A\sin\omega\times 0+B\cos\omega\times 0=B\quad\therefore B=\theta_0\)

つぎに、(8)式を \(t\) で微分して、\(\ t=0\ \)で\(\ \dfrac{d\theta}{dt}=0\ \) とすると

\( \dfrac{d\theta}{dt}=A\omega\cos\omega t-B\omega\sin\omega t\)

\(\qquad =A\omega\cos\omega\times 0-B\omega\sin\omega\times 0=A\omega=0 \)

よって、\(\ A=0\ \)となり、(8)式は\(\quad\theta=\theta_0\cos\omega t\ \) (9)

と決定される。このように解が周期関数で表される振動を単振動といい、単振動で近似出来る振り子を単振り子といいます。

\(\ \omega=\sqrt{\cfrac{g}{l}}\ \) は角振動数 [rad/s] と呼ばれる。

角振動数\(\ \omega\ \)を 2\(\pi\) で割った値は、重りが1秒間に往復する回数を表し、振動数 \(\ f\ \)[Hz}と呼ばれています。

\( f=\dfrac{\omega}{2\pi}=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}\ \,\,\) Hz\(\quad\)(10)

重りが一往復するのに必要な時間は、周期 \(T\) [s] といい、振動数の逆数になる。

\(T=\dfrac{1}{f}=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{l}{g}}\quad\)(11)