\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
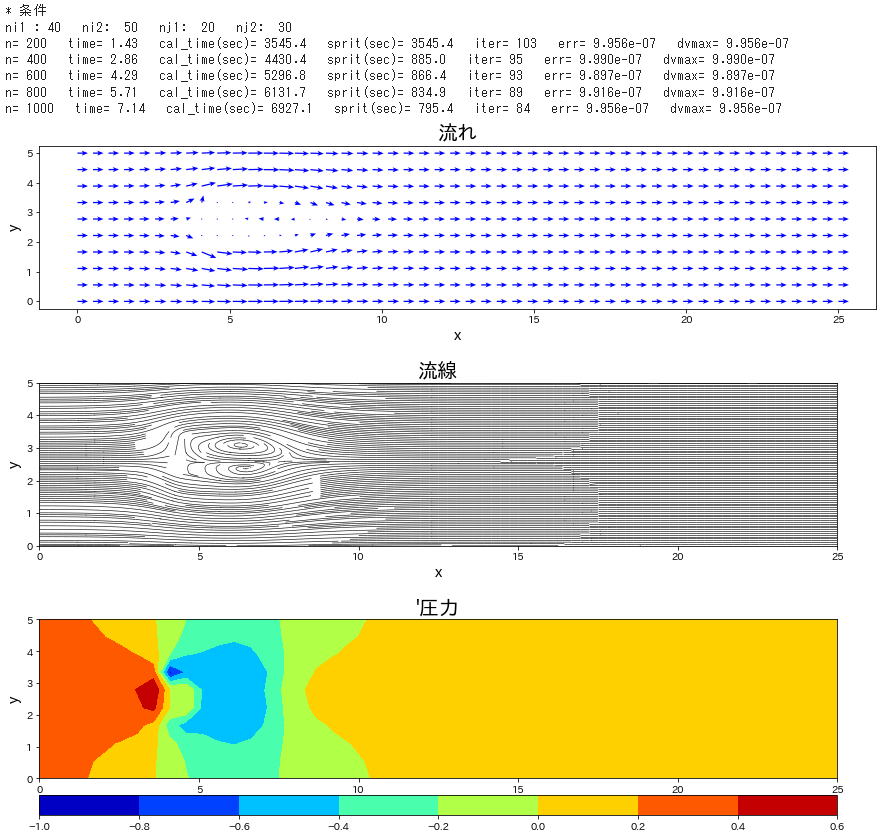
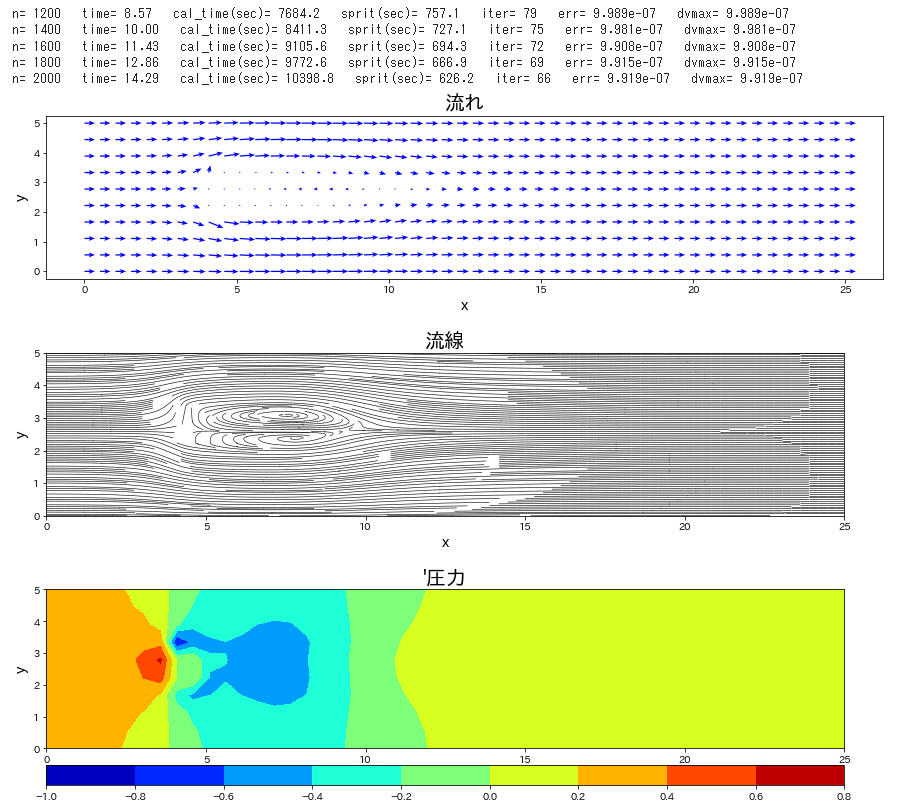
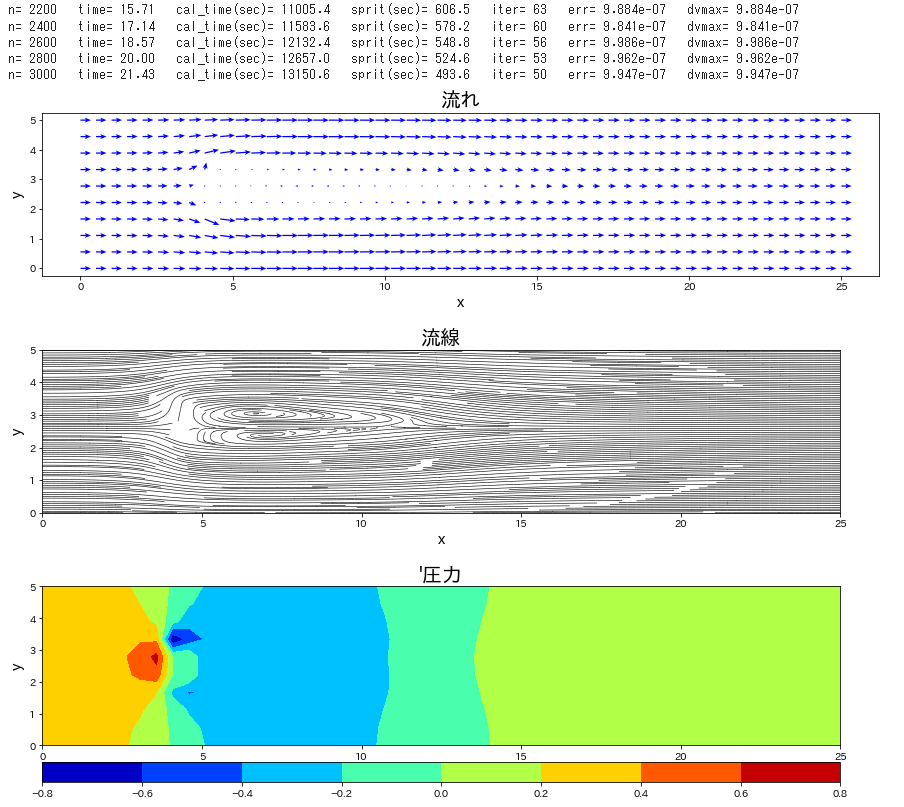
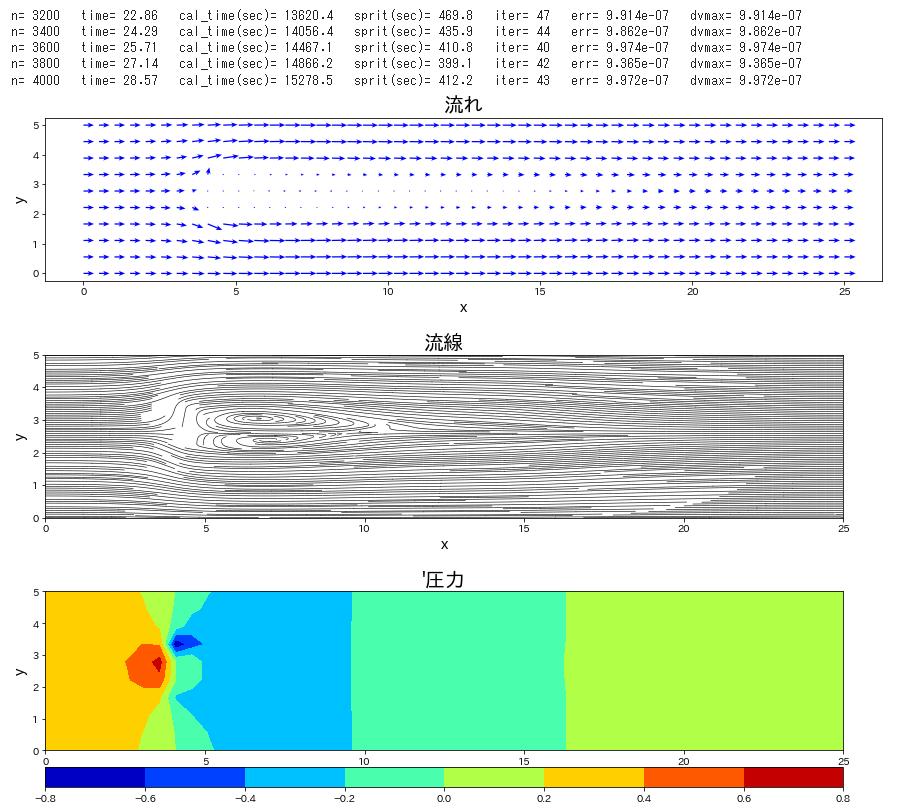
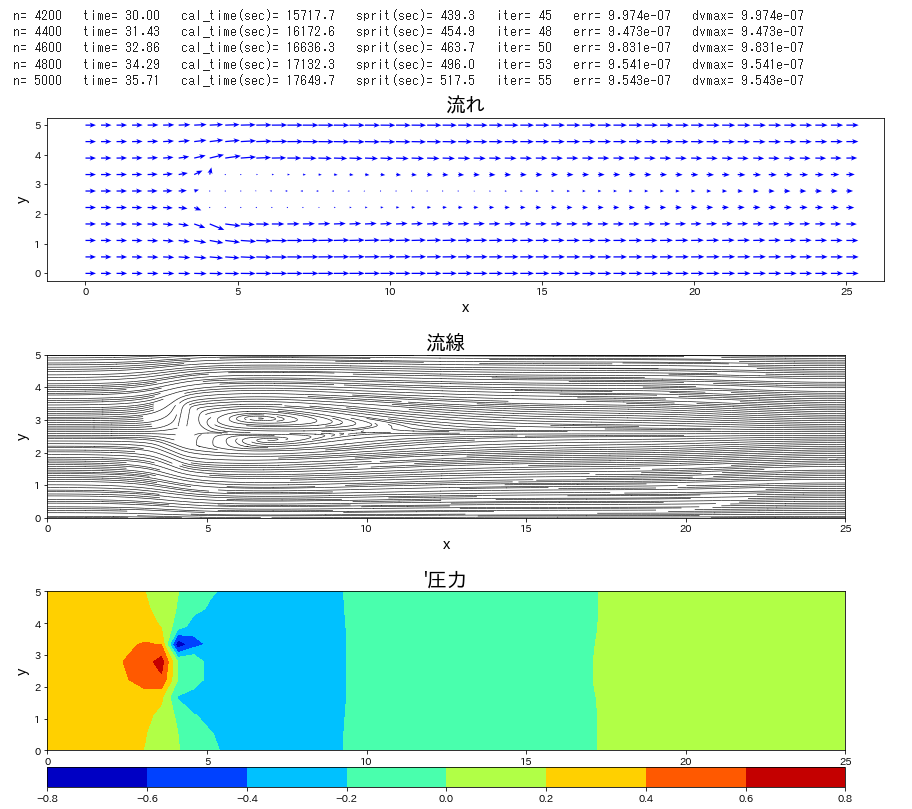
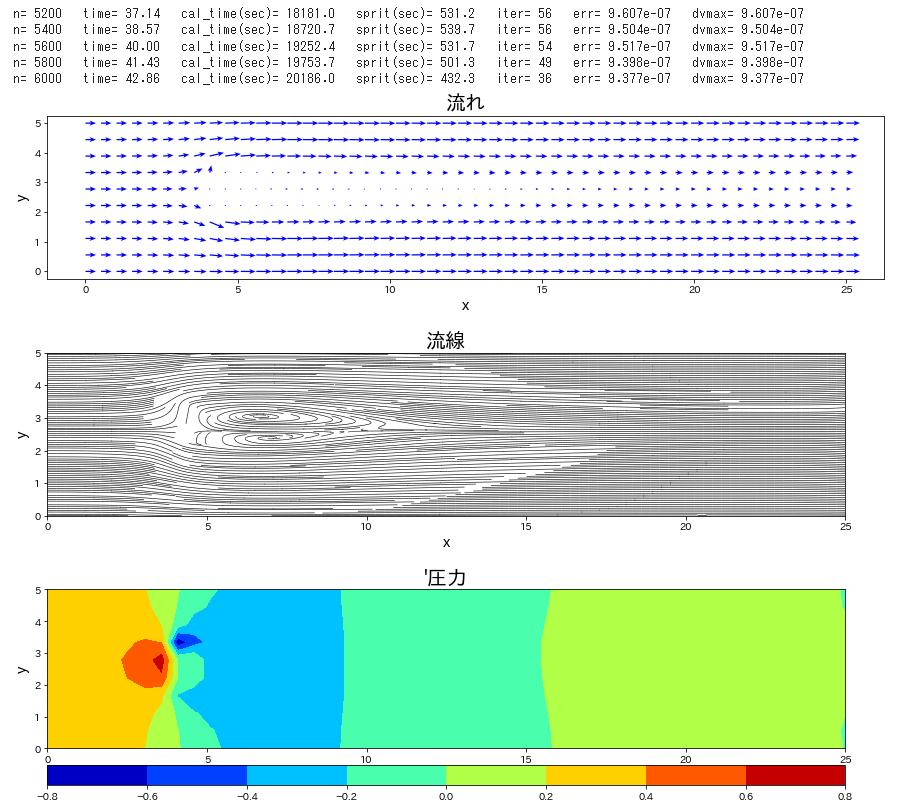
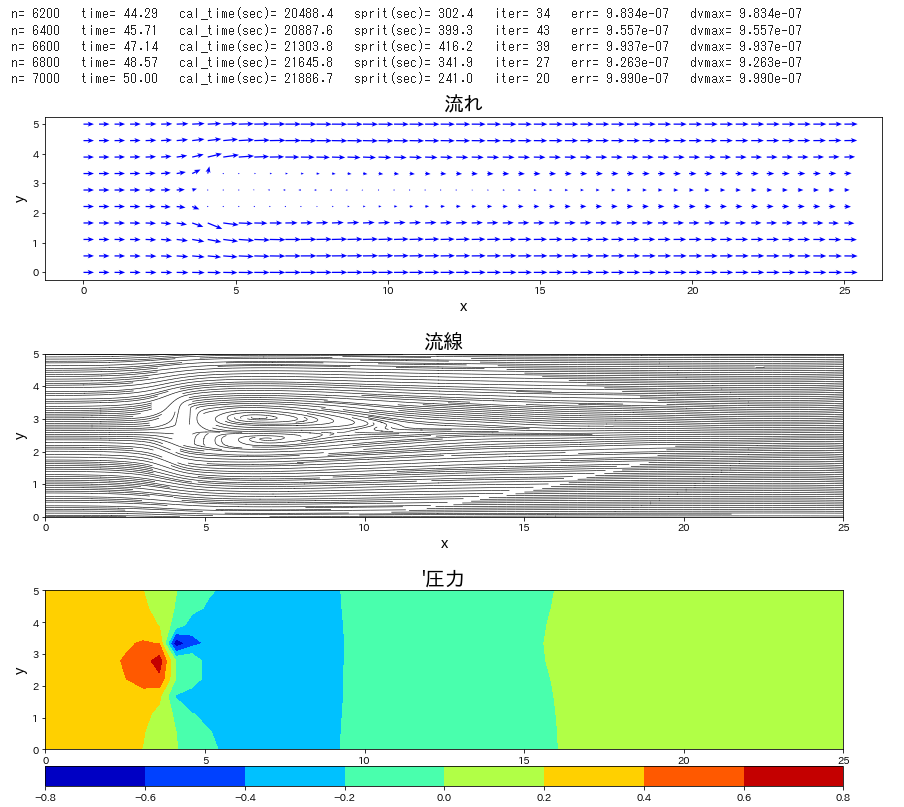
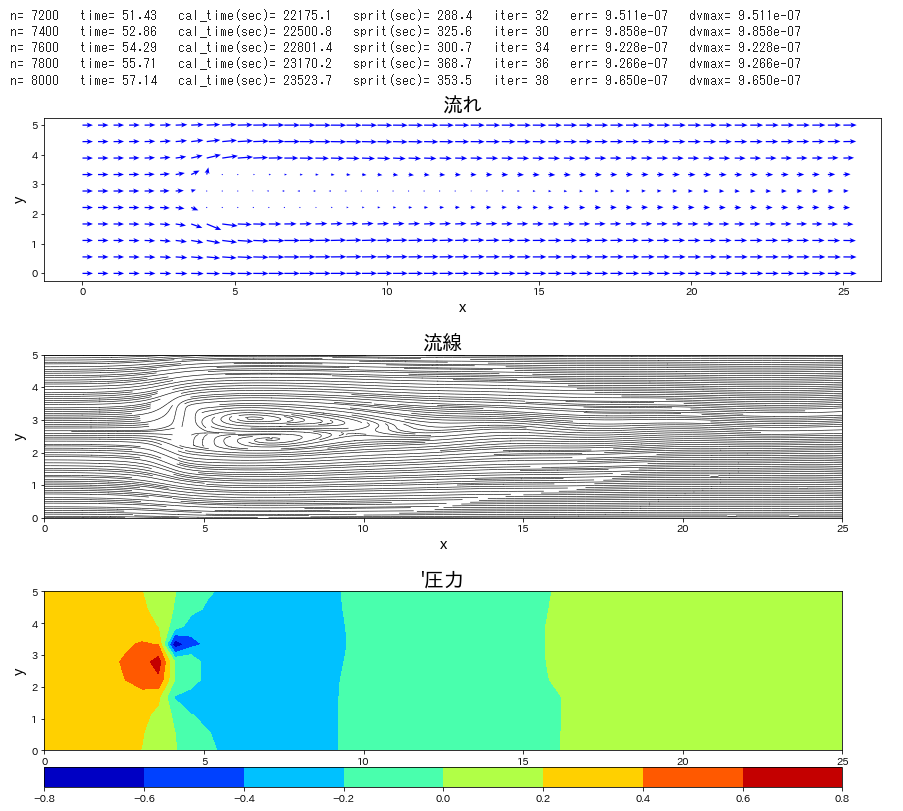
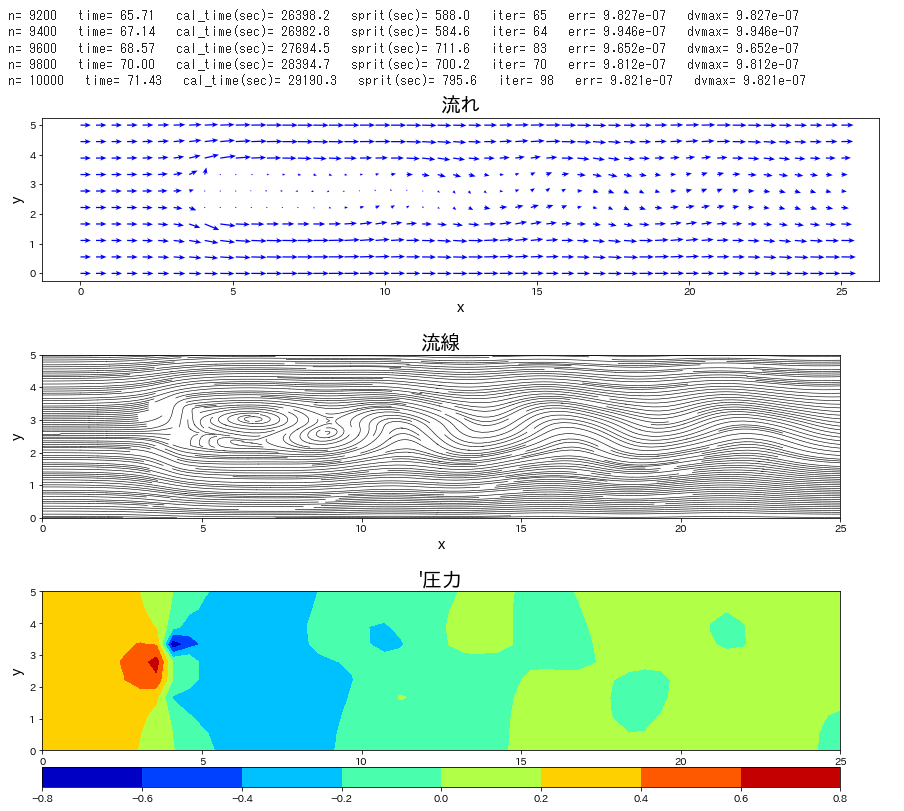
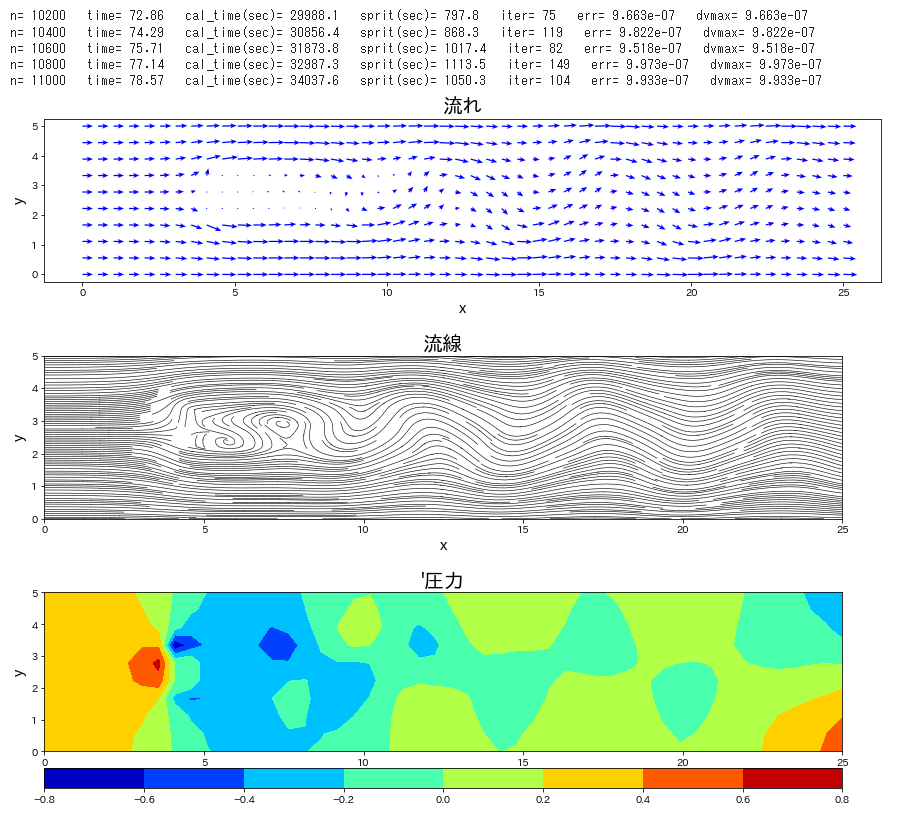
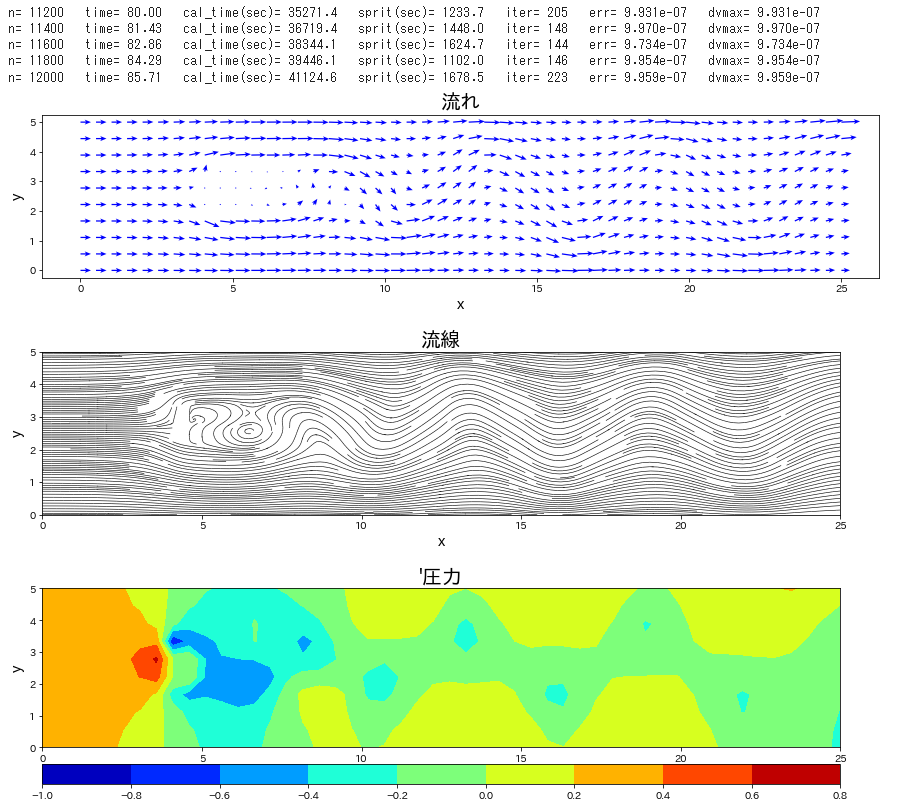
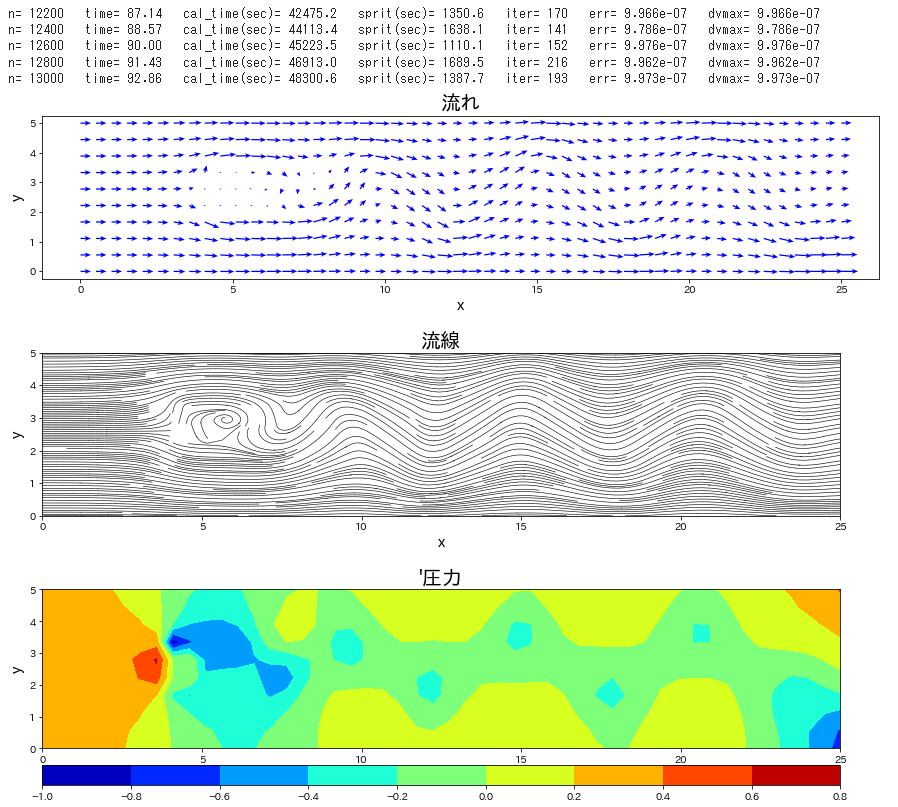
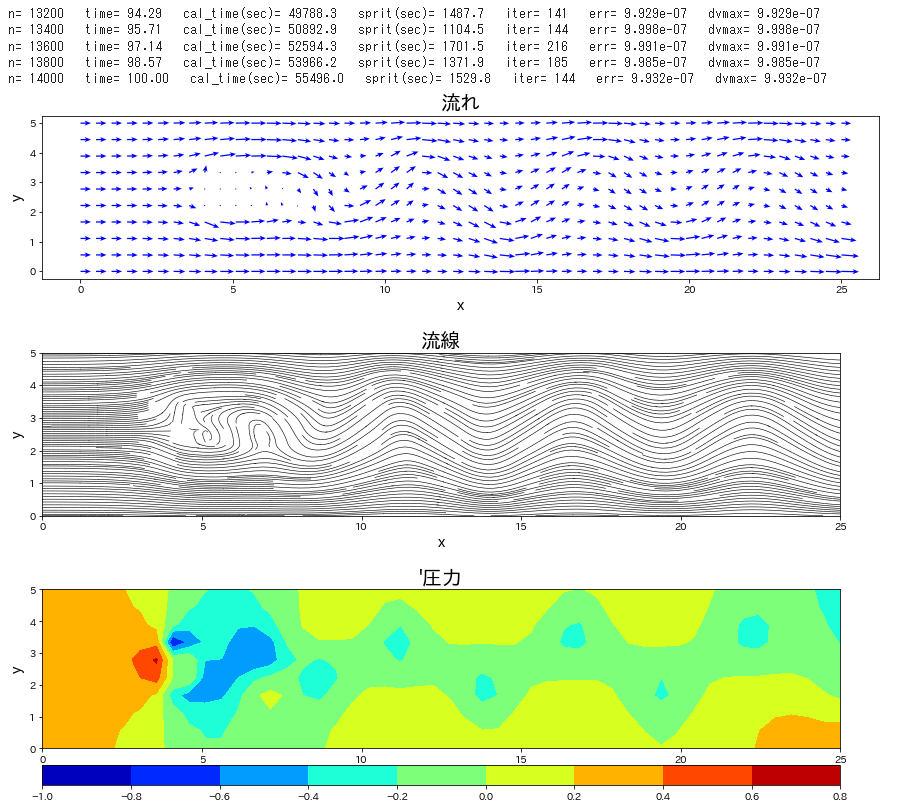
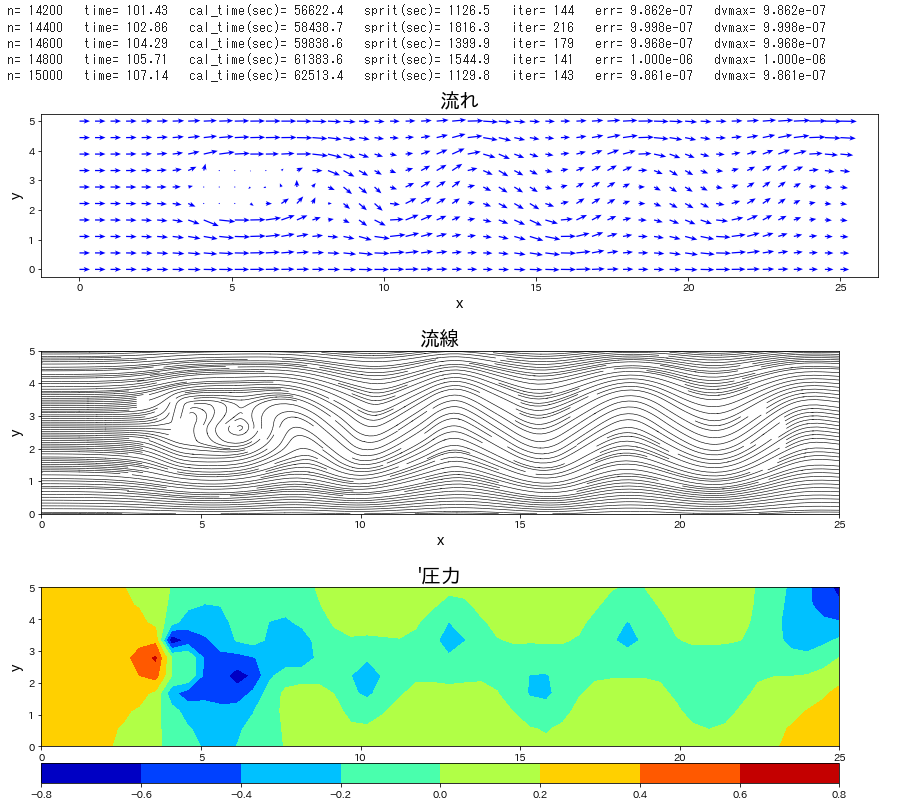
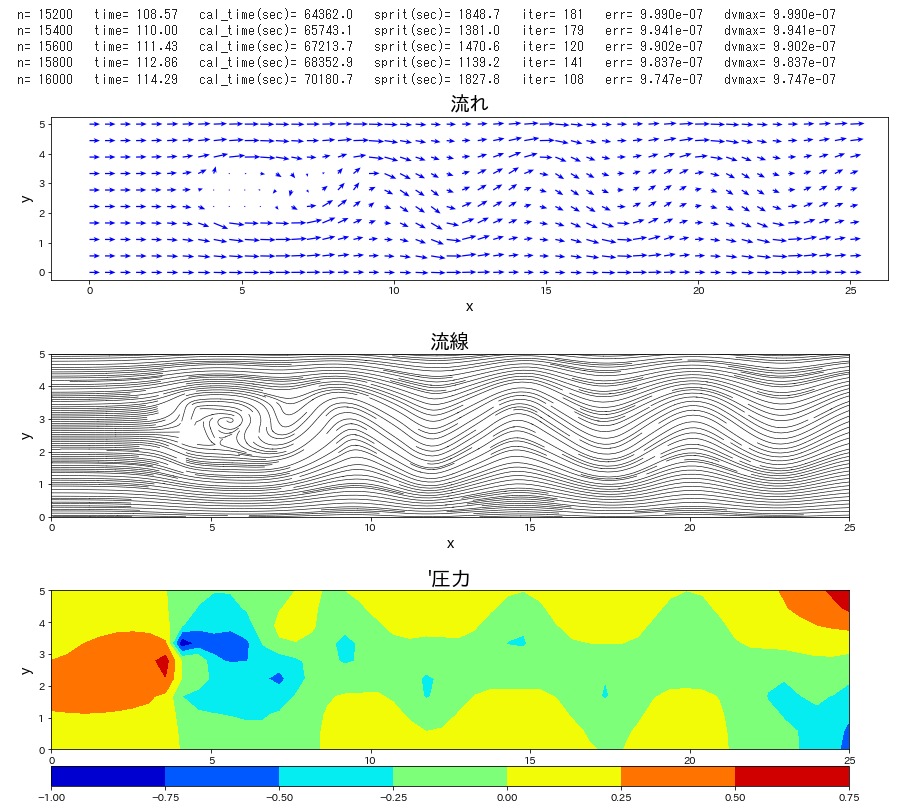
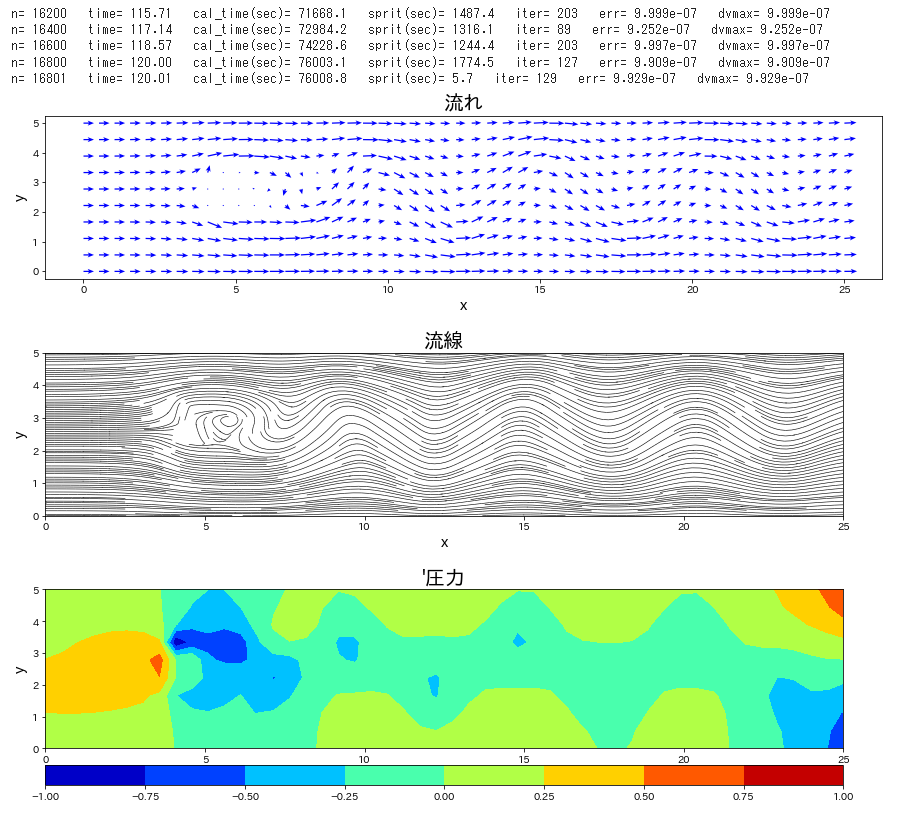
流路にブロックが置かれた条件で、流れの時間発展を計算します。

非圧縮性流体の解析で使用する方程式は以下の2式である。(\(\,\bm{f_B}\,\)は重力や電磁力などの体積力である)
\(\left\{\begin{array}{l}\nabla\cdot\bm{V}=0\hspace{20mm}\cdots\,(1)\\
\pdr{\bm{V}}{t}+(\bm{V}\cdot\nabla)\bm{V}=-\nabla p+\dfrac{1}{\mathrm{Re}}\nabla^2\bm{V}+\bm{f_B}\qquad\cdots\,(2)\end{array}\right.\)
出口条件の\(\,U_c\,\)は出口断面の平均速度とし、入口速度\(\,U_{in}\,\)に等しい。また流れ方向の圧力勾配は\(\,0\,\)とする。この条件を前進オイラー法と1次風上差分により、離散化したのが次の式である。
\(\left\{\begin{array}{l}u_{N_i\,,\,j}^{n+1}=u_{N_i\,,\,j}^n-U_c\dfrac{u_{N_i\,,\,j}^n-u_{N_i-1\,,\,j}^n}{\varDelta x}\varDelta t\hspace{20mm}\cdots\,(3)\\
v_{N_i+1\,,\,j}^{n+1}=v_{N_i+1\,,\,j}^n-U_c\dfrac{v_{N_i+1\,,\,j}^n-v_{N_i-1\,,\,j}^n}{\varDelta x}\varDelta t\hspace{20mm}\cdots\,(4)\\
p_{N_i\,,\,j}^{\,\prime}=p_{N_i\,,\,j}^{\,\prime}\hspace{20mm}\cdots\,(5)\end{array}\right.\)
圧力に関し、流出境界で法線方向の勾配$\,0\,$とするため、圧力補正に関する境界条件が計算領域全周で勾配\(\,0\,\)のノイマン型となる。このため、計算領域全体での流入流量と流出流量が一致していないと、圧力補正に関するポアソン方程式
\(\nabla^2p^{\,\prime}=\dfrac{1}{\mathrm{Re}\varDelta t}\nabla\cdot\bm{V}^*\hspace{20mm}\cdots\,(6)\)
が破綻する。そこで断面平均速度$\,\bar{u}_i\,$を次の式で定義し、
\(\bar{u}_i=\di\sum_{j=1}^{N_i}u_{i\,,\,j}\,\,/\,N_j\hspace{20mm}\)出口速度を次のように修正する。\(\hspace{20mm}u_{N_i\,,\,j}=\,u_{N_i\,,\,j}\,\dfrac{U_{in}}{\bar{u}_{N_i}}\hspace{20mm}\cdots\,(7)\)
Re 数を \(40\) と低めで設定し、時間刻み係数\(\,C_n\,\)を\(\,0.1\,\)とし、圧力補正のポアソン方程式は SOR法 にて解法した。この緩和係数を 1.85 とした。静止状態から流入して時間 120 までの時間発展を計算した。ポアソン方程式の解法に、ほとんどの計算を費やすことになった。Cでコンパイルしたものは、20秒で計算終了したが、Python では 21時間必要であった。
◆ 参考文献
- 数値流体解析の基礎:肖 鋒、長崎 孝夫(2020)、コロナ社
- 流体力学第2版:杉山 弘、遠藤 剛、新井 隆景(2014)、森北出版
import numpy as np
from matplotlib import pyplot as plt
import japanize_matplotlib
import warnings
import time
# 警告非表示
warnings.simplefilter('ignore')
# ------- 条件設定
ni = 250 # 分割数 X
nj = 50 # Y
Lx = 25 # 計算領域のサイズ X
Ly = 5 # Y
Lb = 1 # ブロックの幅
Lx1 = 4 # 入口からブロックまでの距離
scheme =1 # 中心差分 cn=0.1 2: 風上 cn=0.5 3: ハイブリッド cn=0.5
cn = 0.1 # クーラン数 CFL 条件 < 1 scheme=1 の場合
re = 100. # レイノルズ数
uin = 1. # 流入速度
endtime = 120 # 処理終了時間
visc = 1. / re # 粘度
flg = 1 # 処理フラッグ
dx = Lx / float(ni) # セルの大きさ X
dy = Ly / float(nj) # Y
dxi = 1. / dx
dyi = 1. / dy
dxi2 = dxi * dxi
dyi2 = dyi * dyi
dt = cn / (uin * dxi + 2 * visc * (dxi2 + dyi2)) # 時間刻み
ni1 = int(Lx1 * dxi + 1e-6) # ブロックまでのXセル数
ni2 = int((Lx1 + Lb) * dxi + 1e-6) # ブロックの後端までのXセル数
nj1 = int((Ly / 2 - Lb / 2) * dyi + 1e-6) # ブロック部分の通り道の上部セル数
nj2 = int((Ly / 2 + Lb / 2) * dyi + 1e-6) # 下部セル数
alpha = 1.85 # SOR法の緩和係数
eps = 1.e-6 # 繰り返し演算打ち切り誤差
vdx = visc * dxi
vdy = visc * dyi
# -------- 配列
u = np.zeros((ni+2,nj+2)) # 流速 u
v = np.zeros((ni+2,nj+2)) # v
un = np.zeros((ni+2,nj+2)) # 新流速 u
vn = np.zeros((ni+2,nj+2)) # v
p = np.zeros((ni+2,nj+2)) # 圧力
pc = np.zeros((ni+2,nj+2)) # 圧力補正
fe = np.zeros((ni+2,nj+2)) # 検査体積右界面 流速
fn = np.zeros((ni+2,nj+2)) # 上界面 流速
a_e = np.zeros((ni+2,nj+2)) # ポアソン方程式係数東
a_w = np.zeros((ni+2,nj+2)) # 西
a_n = np.zeros((ni+2,nj+2)) # 北
a_s = np.zeros((ni+2,nj+2)) # 南
ap = np.zeros((ni+2,nj+2)) # 圧力
b = np.zeros((ni+2,nj+2)) # div(u)
iu = np.zeros((ni+2,nj+2),dtype=np.int32) # 処理フラッグ u
iv = np.zeros((ni+2,nj+2),dtype=np.int32) # v
ip = np.zeros((ni+2,nj+2),dtype=np.int32) # p
# グラフ条件設定
nxh = ni // 5
nyh = nj // 5
uc = np.zeros((nyh,nxh)) # ベクトル表示用 u
vc = np.zeros((nyh,nxh)) # ベクトル表示用 v
x, y = np.meshgrid(np.linspace(0, Lx, nxh), np.linspace(0, Ly, nyh))
pd = np.zeros((nyh,nxh)) # 圧力表示用
xp, yp = np.meshgrid(np.linspace(0, Lx, nxh), np.linspace(0, Ly, nyh))
# -------- 初期設定
#
# 流れ u
for i in range(1,ni):
for j in range(1,nj+1):
iu[i][j] = flg # 全体に flg 設定
for i in range(ni1,ni2+1):
for j in range(nj1+1,nj2+1):
iu[i][j] = 0 # ブロック部分は設定なし
# 流れ v
for i in range(1,ni+1):
for j in range(1,nj):
iv[i][j] = flg # 全体に flg 設定
for i in range(ni1+1,ni2+1):
for j in range(nj1,nj2+1):
iv[i][j] = 0 # ブロック部分は設定なし
# 圧力 p
for i in range(1,ni+1):
for j in range(1,nj+1):
ip[i][j] = flg # 全体にフラッグ設定
for i in range(ni1+1,ni2+1):
for j in range(nj1+1,nj2+1):
ip[i][j] = 0 # ブロック部分は設定なし
# 圧力ポアソン方程式の係数設定
for i in range(1,ni+1):
for j in range(1,nj+1):
a_w[i][j] = dxi2 # 西
a_e[i][j] = dxi2 # 東
a_s[i][j] = dyi2 # 南
a_n[i][j] = dyi2 # 北
ap[i][j]= (dxi2 + dyi2) * 2
if j==1: # 北側
ap[i][j] = ap[i][j] - a_s[i][j]
a_s[i][j] = 0
if j==nj: # ブロックの上
ap[i][j] = ap[i][j] - a_n[i][j]
a_n[i][j] = 0
if i==1: # 入口 東側
ap[i][j] = ap[i][j] - a_w[i][j]
a_w[i][j] = 0
if i==ni: # ブロックの西側
ap[i][j] = ap[i][j] - a_e[i][j]
a_e[i][j] = 0
# ブロックに隣接するセルの係数変更
for i in range(ni1+1,ni2+1):
j = nj1
ap[i][j] = ap[i][j] - a_n[i][j]
a_n[i][j] = 0
j = nj2+1
ap[i][j] = ap[i][j] - a_s[i][j]
a_s[i][j] = 0
for j in range(nj1+1,nj2+1):
i = ni1
ap[i][j] = ap[i][j] - a_e[i][j]
a_e[i][j] = 0
i = ni2+1
ap[i][j] = ap[i][j] - a_w[i][j]
a_w[i][j] = 0
# 流入境界の速度設定
for j in range(1,nj+1):
u[0][j] = uin
un[0][j] = uin
# 初期速度場
for i in range(1,ni):
for j in range(1,nj+1):
if iu[i][j] == flg:
if i >= ni1 and i<= ni2:
u[i][j] = uin * Ly / (Ly - Lb)
else:
u[i][j] = uin
for j in range(1,nj+1):
u[ni][j] = uin # 出口の流速
print("* 条件")
print("ni1 :",ni1," ni2: ",ni2," nj1: ",nj1," nj2: ",nj2)
st_time=time.time()
old_time=st_time
# ----------- 時間前進 計算ループ -------------------------
n = 0
lp_time = 0
while lp_time <= endtime: # 制限時間内か
n = n + 1
lp_time = lp_time + dt
# -- 境界条件
for i in range(1,ni+1):
u[i][0] = u[i][1] # 下境界 du/dy=0
u[i][nj+1] = u[i][nj] # 上境界 du/dy=0
for j in range(1,nj+1):
v[0][j]= -v[1][j] # 左境界 v=0
p[ni+1][j] = p[ni][j] # 右境界 dp/dx=0
# -- NS方程式: n+1 の仮速度算出
# un
for i in range(ni+1): # 流れ U
for j in range(nj+1):
u0 = (u[i][j] + u[i+1][j]) / 2
v0 = (v[i][j] + v[i+1][j]) / 2
if scheme == 1:
# 中心差分
fe[i][j] = u0 * (u[i+1][j] + u[i][j]) / 2 \
- vdx * (u[i+1][j] - u[i][j])
fn[i][j] = v0 * (u[i][j+1] + u[i][j]) / 2 \
- vdy * (u[i][j+1] - u[i][j])
elif schema == 2:
# 一次風上差分
fe[i][j] = u0 * (u[i+1][j] + u[i][j]) / 2 \
- (vdx + abs(u0)/2) * (u[i+1][j] - u[i][j])
fn[i][j] = v0 * (u[i][j+1] + u[i][j]) / 2 \
- (vdy + abs(v0)/2) * (u[i][j+1] - u[i][j])
else:
# ハイブリッド
fe[i][j] = u0 * (u[i+1][j] + u[i][j]) / 2 \
- max(vdx, abs(u0)/2) * (u[i+1][j] - u[i][j])
fn[i][j] = v0 * (u[i][j+1] + u[i][j]) / 2 \
- max(vdy, abs(v0)/2) * (u[i][j+1] - u[i][j])
# -- 角柱の上下面の処理
for i in range(ni1,ni2+1):
fn[i][nj1] = vdy * 2 * u[i][nj1]
fn[i][nj2] = -vdy * 2 * u[i][nj2+1]
# -- 次の時刻の流れ un
for i in range(1,ni+1):
for j in range(1,nj+1):
if iu[i][j] == flg:
dudt = (fe[i-1][j] - fe[i][j]) * dxi \
+ (fn[i][j-1] - fn[i][j]) * dyi
un[i][j] = u[i][j] + dudt * dt \
+ (p[i][j] - p[i+1][j]) * dxi * dt
# vn
for i in range(ni+1): # 流れ V
for j in range(nj):
u0 = (u[i][j] + u[i][j+1]) / 2
v0 = (v[i][j] + v[i][j+1]) / 2
if scheme == 1:
# 中心差分
fe[i][j] = u0 * (v[i+1][j] + v[i][j]) / 2 \
- vdx * (v[i+1][j] - v[i][j])
fn[i][j] = v0 * (v[i][j+1] + v[i][j]) / 2 \
- vdy * (v[i][j+1] - v[i][j])
elif schema == 2:
# 一次風上差分
fe[i][j] = u0 * (v[i+1][j] + v[i][j]) / 2 \
- (vdx + abs(u0)/2) * (v[i+1][j] - v[i][j])
fn[i][j] = v0 * (v[i][j+1] + v[i][j]) / 2 \
- (vdy + abs(v0)/2) * (v[i][j+1] - v[i][j])
else:
# ハイブリッド
fe[i][j] = u0 * (v[i+1][j] + v[i][j]) / 2 \
- max(vdx, abs(u0)/2) * (v[i+1][j] - v[i][j])
fn[i][j] = v0 * (v[i][j+1] + v[i][j]) / 2 \
- max(vdy, abs(v0)/2) * (v[i][j+1] - v[i][j])
# -- 角柱の上下面の処理
for j in range(nj1,nj2+1):
fe[ni1][j] = vdx * 2 * v[ni1][j]
fe[ni2][j] = -vdx * 2 * v[ni2+1][j]
# -- 次の時刻の値 vn
for i in range(1,ni+1):
for j in range(1,nj):
if iv[i][j] == flg:
dvdt = (fe[i-1][j] - fe[i][j]) * dxi \
+ (fn[i][j-1] - fn[i][j]) * dyi
vn[i][j] = v[i][j] + dvdt * dt \
+ (p[i][j] - p[i][j+1]) * dyi * dt
# -- 流出境界の速度 u
umean = 0
for j in range(1,nj+1):
un[ni][j] = u[ni][j] - uin * (u[ni][j] - u[ni-1][j]) * dxi * dt
umean += un[ni][j]
umean = umean / nj
for j in range(1,nj+1):
if umean != 0:
un[ni][j] = un[ni][j] / umean * uin
else:
un[ni][j] += uin
# -- 速度の発散 div
for i in range(1,ni+1):
for j in range(1,nj+1):
b[i][j] = -((un[i][j] - un[i-1][j]) * dxi \
+ (vn[i][j] - vn[i][j-1]) * dyi) / dt
pc[i][j] = 0 # 圧力補正クリア
# -- 圧力補正の計算 ( SOR 法 )
for iter in range(1,10001):
err = 0
for i in range(1,ni+1):
for j in range(1,nj+1):
if ip[i][j] == flg:
pcn = (a_w[i][j] * pc[i-1][j] + a_e[i][j] * pc[i+1][j] \
+ a_s[i][j] * pc[i][j-1] + a_n[i][j] * pc[i][j+1] + b[i][j]) / ap[i][j]
err = max(err, abs(pcn - pc[i][j]))
pc[i][j] = pc[i][j] + alpha * (pcn - pc[i][j])
if err < eps:
break
# -- 速度、圧力を修正し、前の値を更新する
dvmax = 0.
for i in range(1,ni+1):
for j in range(1,nj+1):
vold = v[i][j]
if iu[i][j] == flg:
u[i][j] = un[i][j] + (pc[i][j] - pc[i+1][j]) * dxi * dt
if iv[i][j] == flg:
v[i][j] = vn[i][j] + (pc[i][j] - pc[i][j+1]) * dyi * dt
p[i][j] = p[i][j] + pc[i][j]
dvmax = max(dvmax, abs(v[i][j]-vold))
# -- 流出境界速度
for j in range(1,nj):
v[ni+1][j] = v[ni+1][j] - uin * (v[ni+1][j] - v[ni][j]) * dxi *dt
for j in range(1,nj+1):
u[ni][j] = un[ni][j]
# -- 途中結果の表示
if n % 200 == 0 or lp_time >= endtime:
# if n < 5:
now_time=time.time()
cal_time=now_time-st_time
d_time=now_time-old_time
old_time=now_time
print("n=",n," time=",'{:.2f}'.format(lp_time)," cal_time(sec)=",'{:.1f}'.format(cal_time)," sprit(sec)=",'{:.1f}'.format(d_time)," iter=",iter," err=",'{:.3e}'.format(err), " dvmax=",'{:.3e}'.format(err) )
# -- グラフ表示
if n % 1000 == 0 or lp_time >= endtime:
# if n < 5:
for j in range(nyh): # V 速度ベクトル
my = j * 5
for i in range(nxh): # U
mx = i * 5
uc[j][i]=(u[mx+1][my+1]+u[mx+2][my+1])/2. # セルの中心
vc[j][i]=(v[mx+1][my+1]+v[mx+1][my+2])/2.
pd[j][i]=(p[mx+1][my+1]+p[mx+2][my+2])/2.
plt.figure(figsize=(15,3))
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.title("流れ",fontsize=20)
plt.quiver(x,y,uc,vc,color='blue',scale=80,headwidth=4,headaxislength=4,width=0.0015)
plt.show()
plt.figure(figsize=(14.3,3))
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.title("流線",fontsize=20)
plt.streamplot(x, y, uc, vc, density=3, color='k', arrowstyle='-', linewidth=0.6)
plt.show()
plt.figure(figsize=(14.3,3.8))
plt.xlabel("x",fontsize=15)
plt.ylabel("y",fontsize=15)
plt.title("'圧力",fontsize=20)
cont=plt.contourf(xp, yp, pd, cmap='jet')
# plt.colorbar(cont, orientation='horizontal')
plt.colorbar(aspect=40, pad=0.08, shrink=1.0,orientation='horizontal', extend='both')
plt.show()