積分その1
【1】\(\,\,\displaystyle\int_0^{\infty}xe^{-ax}dx\quad\)の計算
\(\quad\displaystyle\int_0^{\infty}xe^{-ax}dx\quad\cdots\,\)(1)
まず、\(\,\displaystyle\int xe^{-ax}dx\,\,\)の不定積分から計算する。
部分積分で考えると
\(\quad\displaystyle\int xe^{-ax}dx=x(-ae^{-ax})+\dfrac{1}{a}\displaystyle\int e^{-ax}dx\)
\(\qquad=-axe^{-ax}+\dfrac{1}{a}\displaystyle\int e^{-ax}dx\quad\cdots\,\)(2)
(1)式の定積分を考える時、まず次の極限を計算する。
\(\quad\displaystyle\lim_{x\to\infty}\dfrac{x}{e^x}\quad\cdots\,\)(3)
\(\quad x\ge 0\,\,\)のとき\(\,\,e^x\ge\dfrac{x^2}{2}\,\,\)を考える。
\(\quad f(x)=e^x-\dfrac{x^2}{2}\quad\cdots\,\)(4)
とすると、\(x\ge 0\quad\)のとき、\(f'(x)\gt 0\,\,,\quad f^{\prime\prime}\gt 0\quad\)なので、\(f(x)\gt 0\quad\)である。よって
\(\,\,e^x\ge\dfrac{x^2}{2}\,\,\)が成り立つ。そこで
\(\quad 0\ge \dfrac{x}{e^x}\ge \dfrac{x}{\frac{x^2}{2}}\quad\)つまり\(\quad 0\ge \dfrac{x}{e^x}\ge \dfrac{2}{x}\quad\)となり、
\(\quad\displaystyle\lim_{x\to\infty}\dfrac{2}{x}=0\quad\)なので\(\quad\displaystyle\lim_{x\to\infty}\dfrac{x}{e^x}=0\quad\cdots\,\)(5)
となる。
この結果 (2)式を\(\,0\,\)から\(\,\infty\,\)まで積分すると
\(\quad\displaystyle\int_0^{\infty}xe^{-ax}dx=\left[-axe^{-ax}\right]_0^{\infty}+\dfrac{1}{a}\displaystyle\int_0^{\infty}e^{-ax}dx\)
\(\qquad =0-0+\dfrac{1}{a}\left[-\dfrac{1}{a}e^{-ax}\right]_0^{\infty}=\dfrac{1}{a^2}\quad\cdots\,\)(6)
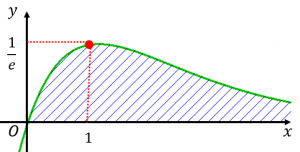 グラフは\(\,y=xe^{-x}\,\)である。\(x\,\to\,\infty\,\)まで積分すると斜線部分の面積は\(\,1\,\)となります。
グラフは\(\,y=xe^{-x}\,\)である。\(x\,\to\,\infty\,\)まで積分すると斜線部分の面積は\(\,1\,\)となります。
|
|
|
|
|