1.経緯
私が通学(通信制なので、通ってはいないが)している放送大学のゼミで、自宅での実験を動画撮影して皆で共有するという企画があったので、振り子の実験をやってみました。
振り子は小学\(5\)年生用の実験セットをAmazonから仕入れました。
 (「ふりこのはたらき」 \(730\)円)
(「ふりこのはたらき」 \(730\)円)
2.実験
 ひもの長さは\(30\)cmとして、振れ角測定用に角度を書いた紙を付けました。大きく振った位置から重りを降ろした。
ひもの長さは\(30\)cmとして、振れ角測定用に角度を書いた紙を付けました。大きく振った位置から重りを降ろした。
(\(2020.09.05\) 実施)
撮影は iPhone をそのままの設定で(\(30\)f)三脚無しで行いました。時間は約\(2\)分間でした。
動画は DropBox 経由で、Windows マシンに落とした。再生で簡単にコマ落としが出来、時間の表示が \(1/100\) 秒単位で出てくるので MovieMaker を使用した。(最近は MovieMaker はサポートされていないようですね)
撮影した動画の抜粋
(このページでは動画のサイズが\(8\)Mb なので抜粋版をつくりました)
3.実験結果
動画をMovieMaker でコマ落とし再生して、最大振幅の角度と時間を記録したのが下図です。
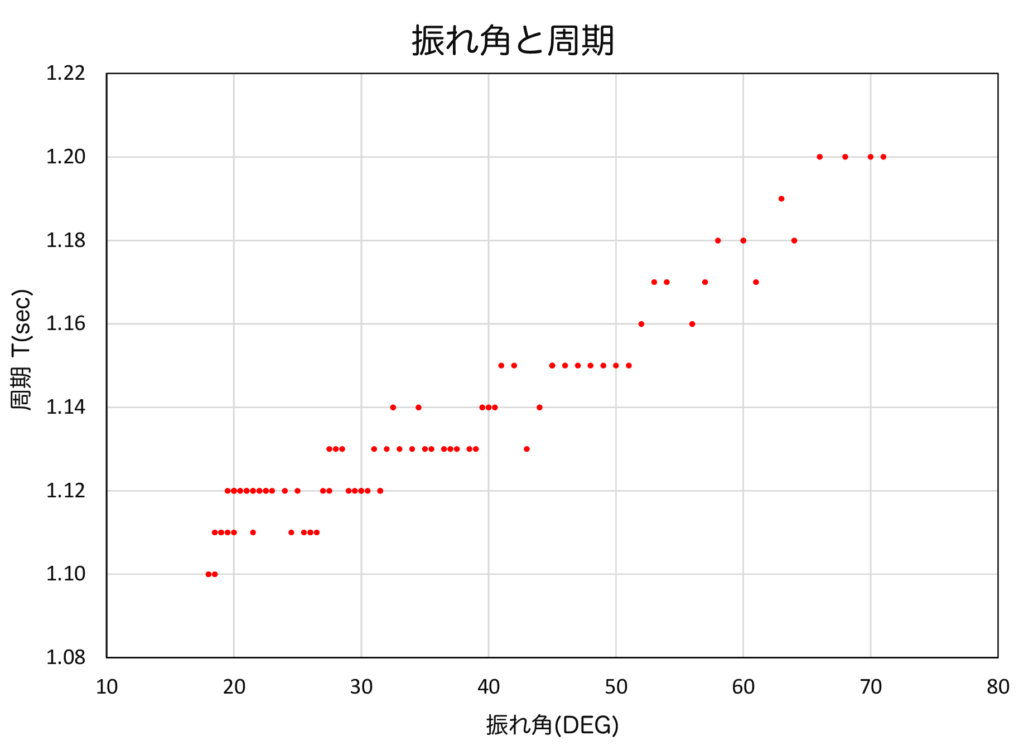
動画が\(30\)fなので、時間刻みが\(1/30\)sec単位となり、グラフは階段状になるが、振れ角が大きいと周期が長いという結果となった。
4.検討1:振幅の小さい場合
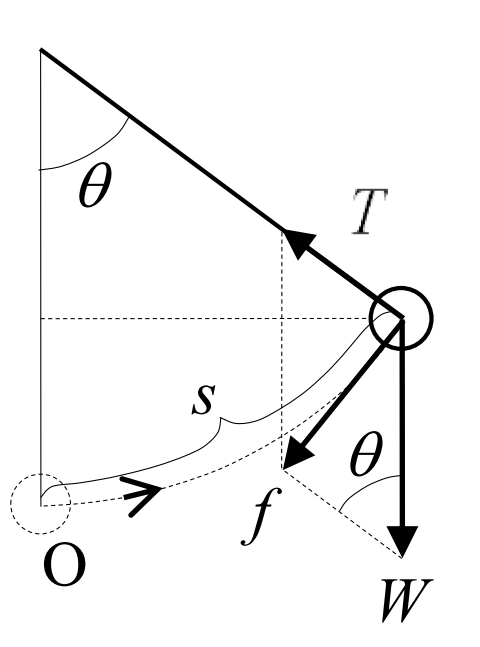 糸の張力\(\,T\,\)、重力\(\,W\,\)の合力\(\,f^{\prime\prime}\)が重りに掛かる。
糸の張力\(\,T\,\)、重力\(\,W\,\)の合力\(\,f^{\prime\prime}\)が重りに掛かる。
\(\quad W=mg\)
\(\quad f^{\prime\prime}=mg\sin\theta\)
円周方向の重りの動く長さを\(\,s\,\)とすると
\(\quad m\dfrac{d^2s}{dt^2}=-mg\sin\theta\)
\(\quad s=l\theta\,\)なので\(\quad\dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\sin\theta\)
振幅が小さいときは
\(\quad\theta\approx\sin\theta\quad\)とすることが出来るので
\(\quad\dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\theta\quad\)とすることが出来、次のような一般解が得られる。
\(\quad\theta=A\sin\sqrt{\dfrac{g}{l}}t+B\cos\sqrt{\dfrac{g}{l}}t\)
ここで初期条件として\(\quad t=0\quad d\theta/dt=0\quad\theta=\theta_0\quad\)とすると
\(\quad\theta=\theta_0\cos\sqrt{\dfrac{g}{l}}t\quad\)が得られる。
周波数\(\,f\,\)は\(\quad f=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}\quad\)となる。
周期\(\,T\,\)は\(\quad T=\dfrac{1}{f}=2\pi\sqrt{\dfrac{l}{g}}\quad\)である。
今回は紐の長さを\(\,30\,\)cm としたので、
\(\quad T=2\times 3.141593\times\sqrt{\dfrac{0.3}{9.80655}}=1.099..\,\)(s) となった。結果のグラフを見ると、振れ角\(20\,\)度以下ではほぼこの周期となっているようである。
5.検討2:振幅が大きい場合
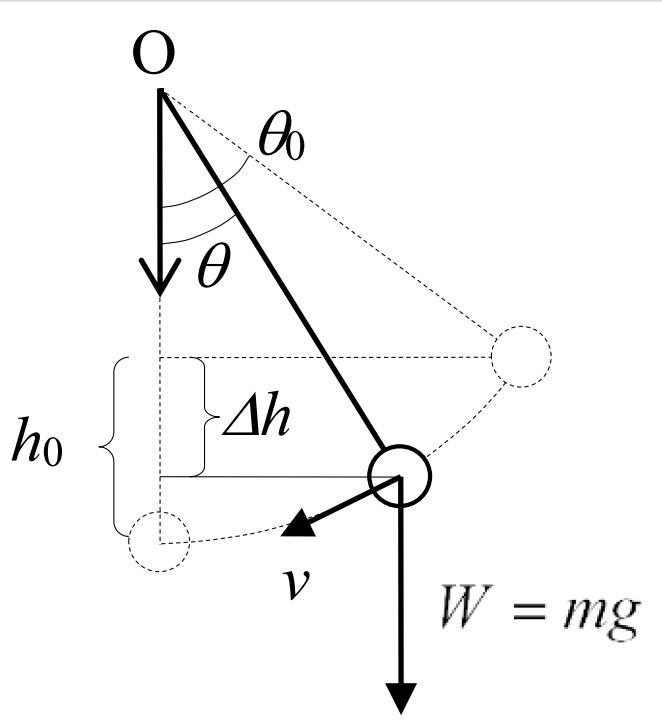 エネルギー保存則を用いて、振幅の大きい振り子の運動を計算する。振り子の最下点を原点とし、振りだし高さを\(\,h_0\,\)、\(\Delta h\,\)だけ降りた点の円周方向の速度を\(\,v\,\)とすると
エネルギー保存則を用いて、振幅の大きい振り子の運動を計算する。振り子の最下点を原点とし、振りだし高さを\(\,h_0\,\)、\(\Delta h\,\)だけ降りた点の円周方向の速度を\(\,v\,\)とすると
\(\quad\dfrac{1}{2}mv^2=mgl(\cos\theta-\cos\theta_0)\quad\)なので
\(\quad\therefore v=\sqrt{2gl(\cos\theta-\cos\theta_0)}\)
ここで、\(\,v=\dfrac{ds}{dt}=l\dfrac{d\theta}{dt}\quad\)なので
\(\quad l\dfrac{d\theta}{dt}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\)より
\(\quad dt=\sqrt{\dfrac{l}{2g}}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\)
これを積分すると周期を求めることが出来る。
\(\,t\,\)の積分範囲を\(\,4\,\)分の\(\,1\,\)周期とすると、\(\theta=0\,\to\,\theta_0\)
\(\displaystyle\int^{\frac{T}{4}}_0dt=\dfrac{T}{4}=\sqrt{\dfrac{l}{2g}}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\)
ここからの積分は振り子の計算その2を参考にしてください。
プロセスとしては\(\quad\sin\phi=\sin(\theta/2)/\sin(\theta_0/2)\quad\)とおいて、いくつかの計算を経て以下の積分となる。
\(\quad T=4\sqrt{\dfrac{l}{g}}\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{d\phi}{\sqrt{1-\sin^2(\theta_0/2)\sin^2\phi}}\)
この積分は楕円積分と呼ばれる。
5.1 楕円積分の計算
楕円積分を参照のこと。
第1種の楕円積分は以下のような式となる。
\(\quad I=\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{d\phi}{\sqrt{1-a^2\sin^2\phi}}=\dfrac{\pi}{2}\displaystyle\sum_{n=0}^{\infty}\left\{\dfrac{2n-1)!!}{2n!!}\right\}^2a^{2n}\)
ここで\(\quad n!!\quad\)は二重階乗である。
これより、\(\,T\quad\)は以下のようになる。
\(\quad T=4\sqrt{\dfrac{l}{g}}\displaystyle\int_0^{\frac{\pi}{2}}\frac{d\phi}{\sqrt{1-\sin^2(\theta_0/2)\sin^2\phi}}\)
\(\qquad=2\pi\sqrt{\dfrac{l}{g}}\displaystyle\sum_{n=0}^{\infty}\left\{\dfrac{(2n-1)!!}{2n!!}\right\}^2\left(\sin\dfrac{\theta_0}{2}\right)^{2n}\)
具体的な計算は\(\quad b=\sin\dfrac{\theta_0}{2}\quad\)とおいて、振り子の長さ\(\,l=0.3\,\)m を使うと
\(\quad T=2\pi\sqrt{\dfrac{l}{g}}\left\{1+\left(\dfrac{1}{2}\right)^2b^2+\left(\dfrac{1}{2}\dfrac{3}{4}\right)^2b^4+\left(\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{6}\right)^2b^6\right.\)
\(\qquad\qquad\qquad \left.+\left(\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{6}\dfrac{7}{8}\right)^2b^8+\left(\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{6}\dfrac{7}{8}\dfrac{9}{10}\right)^2b^{10}+\cdots\,\right\}\)
\(\qquad=1.099\times\left\{1+\dfrac{1}{4}b^2+\dfrac{9}{64}b^4+\dfrac{25}{256}b^6+\dfrac{1225}{16384}b^8\right.\)
\(\qquad\qquad\qquad\left.+\dfrac{3969}{65536}b^{10}+\dfrac{53361}{1048576}b^{12}+\cdots\,\right\}\)
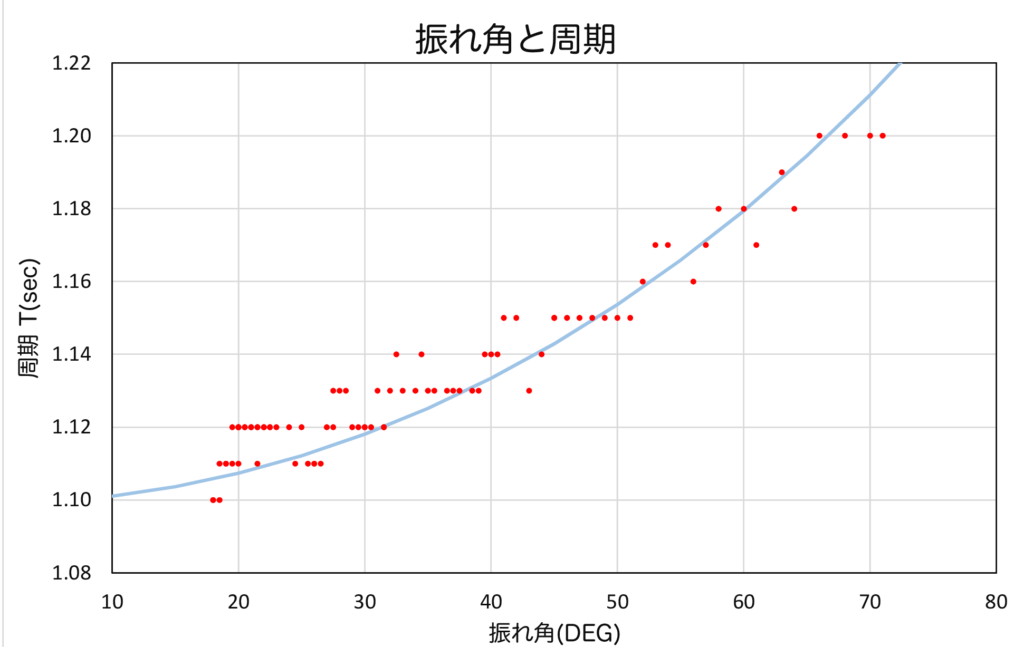
この値と実験結果を併せて表示する。
|
|
|
|
|
測定データが \(\quad 1/30\,\)sec 単位であるが、まあ妥当な結果となったようである。