ひもの両端を持って垂らしたときにできる曲線を懸垂曲線( カテナリー catenary )といいますが、この曲線の方程式を導いてみる。
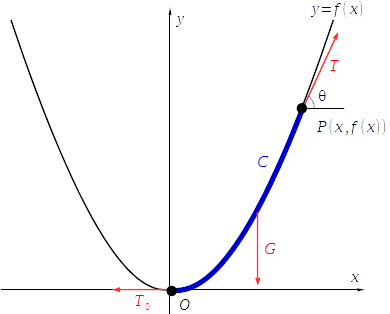 ひもの底を原点\(O\,\)とし、水平方向に\(x\,\)軸、鉛直方向に\(y\,\)軸をとる。ひもの曲線を\(\,y=f(x)\,\)とおいて関数\(\,f(x)\,\)を求める。
ひもの底を原点\(O\,\)とし、水平方向に\(x\,\)軸、鉛直方向に\(y\,\)軸をとる。ひもの曲線を\(\,y=f(x)\,\)とおいて関数\(\,f(x)\,\)を求める。
ひもの\(\,x>0\,\)の部分に点\(\,(x,f(x))\,\)をとり、これを\(P\,\)とします。また、ひもの\(O\,\)から\(P\,\)の部分(両端を含む)を\(C\,\)とします。
【\(\,f(x)\,\)に対する微分方程式を立てる】
ひもの一部\(\,C\,\)に加わる力の釣り合いの式から\(\,f(x)\,\)についての微分方程式を立てる。\(C\,\)には次の3つの力が加わっている。
- 点\(\,O\,\)に水平方向のひもの張力\(\,T_0\)
- 点\(\,P\,\)に接線方向上向きにひもの張力\(\,T\)
- \(\,C\,\)の重心に鉛直下向きに重力\(\,G\)
ここで、原点にはたらく張力\(\,T_0\,\)は\(\,x\,\)に関係なく一定なので定数とする。
\(T\,\)について、\(P\,\)における\(\,f(x)\,\)の接線と\(\,x\,\)軸の正の部分とのなす角を\(\,\theta\,\)とすると、\(T\,\)の\(\,x\,\)成分、\(y\,\)成分はそれぞれ\(\,T\cos\theta\,,\,T\sin\theta\,\)となる。
この角度\(\,\theta\,\)と\(\,f(x)\,\)は、\(x\,\)における微分が接線なので
\(\quad f'(x)=\tan\theta\quad\)となる。
\(C\,\)の長さを\(\,l\,\)とすると曲線の長さの式から
\(\quad l=\displaystyle\int_0^x\sqrt{1+\{f'(x)\}^2}dx\quad\)で求められる。
線密度を\(\,\rho\,\)、重力加速度を\(\,g\,\)とすると
\(\quad G=\rho lg=\rho g\quad\)となる。
これらより釣り合いの式は以下のようになる。
- 鉛直方向:\(\,T\sin\theta=\rho lg\)
- 水平方向:\(\,T\cos\theta=T_0\)
\(T\,\)を消去して、定数をまとめて \(\,k=\dfrac{\rho g}{T_0}\,\,\)とおくと
\(\quad f'(x)=k\displaystyle\int_0^x\sqrt{1+\{f'(x)\}^2}dx\quad\)となる。
両辺を\(\,x\,\)で微分すると
\(\quad f^{\prime\prime}(x)=k\sqrt{1+\{f'(x)\}^2}\quad\)となる。
境界条件は\(\quad f(0)=0\,\,,\quad f'(0)=0\quad\)となる。
【微分方程式を解く】
この微分方程式を解く。\(\quad z=f'(x)\quad\)とおくと
\(\quad\dfrac{dz}{dx}=k\sqrt{1+z^2}\)
\(\quad\dfrac{dz}{\sqrt{1+z^2}}=k\,dx\quad\)となる。
先程の条件で\(\quad f'(x)=\tan\theta=z\quad\)なので
\(\quad dz=\dfrac{1}{\cos^2\theta}d\theta\quad\)となる。よって、
\(\quad \dfrac{dz}{\sqrt{1+z^2}}=\dfrac{1}{\sqrt{1+\tan^2\theta}}\dfrac{d\theta}{\cos^2\theta}=\dfrac{d\theta}{\sqrt{\dfrac{\cos^2\theta+\sin^2\theta}{\cos^2\theta}}\cos^2\theta}\)
\(\qquad =\dfrac{d\theta}{\cos\theta}\quad\)となる。
このままでは積分出来ないので、\(\quad\dfrac{d}{d\theta}\sin\theta=\cos\theta\quad\)を利用して
\(\quad\dfrac{d\theta}{\cos\theta}=\dfrac{d(\sin\theta)}{\cos^2\theta}=\dfrac{d(\sin\theta)}{(1-\sin\theta)(1+\sin\theta)}\)
\(\quad =\dfrac{1}{2}\left(\dfrac{1}{1-\sin\theta}+\dfrac{1}{1+\sin\theta}\right)\,d(\sin\theta)\quad\)となる。
この形なら積分可能なので\(\,\,\sin\theta\,\,\)で積分する。
\(\quad\displaystyle\int\dfrac{dz}{\sqrt{1+z^2}}=\dfrac{1}{2}\displaystyle\int\left(\dfrac{1}{1-\sin\theta}+\dfrac{1}{1+\sin\theta}\right)\,d(\sin\theta)\)
\(\quad=\dfrac{1}{2}\left\{-\log(1-\sin\theta)+\log(1+\sin\theta)\right\}\)
\(\quad=\dfrac{1}{2}\log\left(\dfrac{1+\sin\theta}{1-\sin\theta}\right)\)
よって\(\quad z=\tan\theta\quad\)として
\(\quad f'(x)=\displaystyle\int\dfrac{dz}{\sqrt{1+z^2}}=\dfrac{1}{2}\log\left(\dfrac{1+\sin\theta}{1-\sin\theta}\right)=kx+C_1\quad\) となる。
境界条件\(\quad f'(x)=0\quad x=0\,\,,\,\theta=0\quad\)より\(\quad C_1=0\,\,\)。
\(\quad\dfrac{1+\sin\theta}{1-\sin\theta}=e^{2kx}\quad\)より、まず\(\quad\sin\theta\quad\)について解く。
\(\quad 1+\sin\theta=e^{2kx}(1-\sin\theta)\qquad (e^{2kx}+1)\sin\theta=e^{2kx}-1\)
\(\quad \sin\theta=\dfrac{e^{2kx}-1}{2^{2kx}+1}\quad\)となる。ここから以下の公式を使う。
\(\quad 1+\dfrac{1}{\tan^2\theta}=\dfrac{\tan^2\theta+1}{\tan^2\theta}=\dfrac{\sin^2\theta+\cos^2\theta}{\sin^2\theta}=\dfrac{1}{\sin^2\theta}\)
\(\quad\dfrac{1}{\tan^2\theta}=\left(\dfrac{e^{2kx}+1}{2^{2kx}-1}\right)^2-1\)
\(\qquad=\dfrac{(e^{2kx}+1)^2-(e^{2kx}-1)^2}{(e^{2kx}-1)^2}\)
\(\qquad=\dfrac{4e^{2kx}}{(e^{2kx}-1)^2}\quad\)より
\(\quad\tan\theta=\dfrac{e^{2kx}-1}{2e^{kx}}=\dfrac{e^{kx}-e^{-kx}}{2}=\sinh kx\)
\(\quad f'(x)=z=\tan\theta=\sinh kx\quad\)なので
\(\quad f(x)=\displaystyle\int\dfrac{e^{kx}-e^{-kx}}{2}dx=\dfrac{e^{kx}+e^{-kx}}{2k}+C_2\)
境界条件が\(\quad f(0)=0\quad\)なので\(\quad C_2=-k\quad\)より
\(\quad f(x)=\dfrac{e^{kx}+e^{-kx}}{2k}-k=\dfrac{\cosh kx-1}{k}\)
|
|
|
|
|