1.プランクの法則 (Planck’s law)
物理学における黒体から輻射(放射)される電磁波の分光放射輝度、もしくはエネルギー密度の波長分布に関する公式。プランクの公式とも呼ばれる。ある温度\(\,T\,\)における黒体からの電磁輻射の分光放射輝度を全波長領域において正しく説明することができる。1900年、ドイツの物理学者マックス・プランクによって導かれた。
プランクはこの法則の導出を考える中で、輻射場の振動子のエネルギーが、あるエネルギー素量(現在ではエネルギー量子と呼ばれている)\(\,\epsilon=h\nu\,\)の整数倍になっていると仮定した。このエネルギーの量子仮説(量子化)はその後の量子力学の幕開けに大きな影響を与えている。
プランクの放射式では、単位振動数\(\,\nu\,\)あたりの黒体輻射強度を以下のように表す。
\(\quad B_{\nu}(T)=\dfrac{2h}{c^2}\dfrac{\nu^3}{e^{h\nu/kT}-1}\quad\cdots\,\)(1)
なお、ここで\(\,c\,\)は光速、\(\,h\,\)はプランク定数、\(\,k\,\) はボルツマン定数である。このプランクの放射式に温度\(\,T\,\)に3000K\(\sim\)7000Kを代入してプロットしたのが下図である。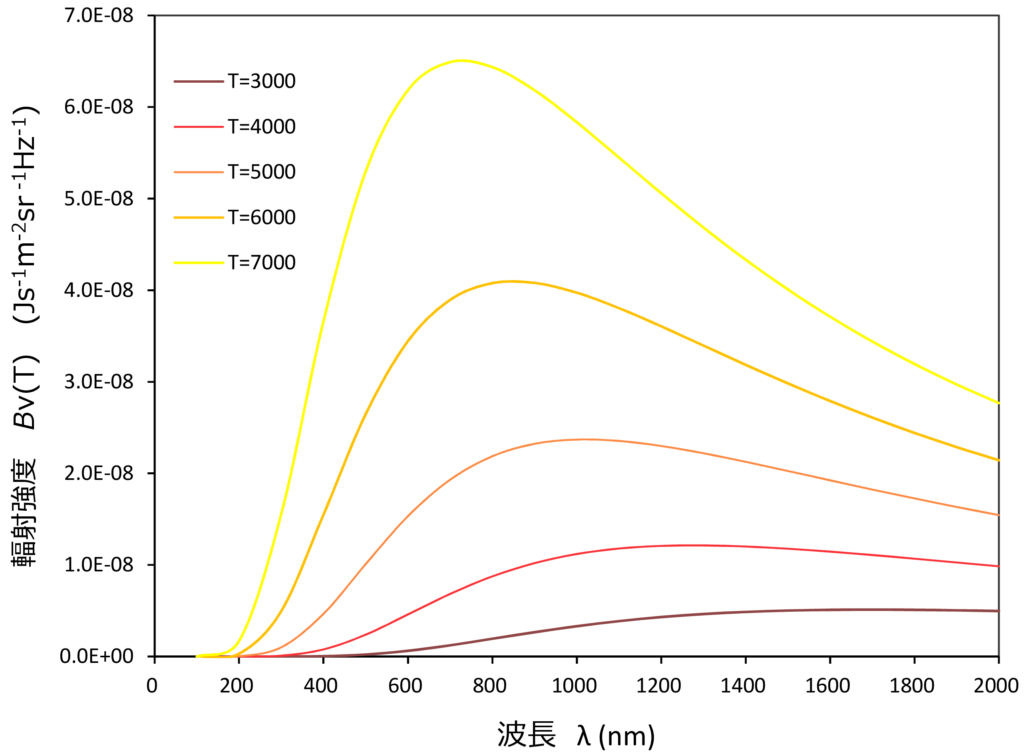
2.全黒体輻射強度 (Total blackbody radiation intensity)
このプランクの放射式を全振動数で積分したものを、全黒体輻射強度\(\,B(T)\,\) という。(1)式で、\(\,x=h\nu/kT\,\)とおくと、
\(\quad B_x(T)=\dfrac{2k^3T^3}{c^2h^2}\dfrac{x^3}{e^x-1}\quad\cdots\,\)(2)
となり、全振動数で積分すると
\(\quad \displaystyle\int_0^{\infty}B_{\nu}(T)d\nu=\displaystyle\int_0^{\infty}B_x(T)\,\dfrac{kT}{h}\,dx\quad\cdots\,\)(3)
\(\quad B(T)=\dfrac{2k^4T^4}{c^2h^3}\displaystyle\int_0^{\infty}\dfrac{x^3}{e^x-1}\,dx\quad\cdots\,\)(4)
(4)式の積分は\(\,\pi^4/15\,\)となるので、
全黒体輻射強度(放射輝度)[単位 Wm\(^{-2}\)sr\(^{-2}\)K\(^{-4}\)] は
\(\quad B(T)=\dfrac{2\pi^4k^4T^4}{15c^2h^3}=\dfrac{\sigma}{\pi}T^4\quad\cdots\,\)(5)
となる。
3.\(\,\,\,\,x^3/e^x-1\,\)の\(\,\,\)積分の計算
\(\quad\dfrac{x^3}{e^x-1}=\dfrac{x^3}{e^x}\dfrac{1}{1-e^{-x}}\quad\cdots\,\)(6)
(6)式の最後の項は公比\(\,e^{-x}\,\)の等比数列の和とすると
\(\quad\dfrac{1}{1-e^{-x}}=1+e^{-x}+e^{-2x}+\cdots\)
となるので
\(\quad\dfrac{x^3}{e^x-1}=x^3(e^{-x}+e^{-2x}+e^{-3x}+\cdots)\quad\cdots\,\)(7)
ここで\(\,x^pe^{-ax}\,\)の形の関数を積分するために、ガンマ関数を利用する。
ガンマ関数の定義から
\(\quad\varGamma(q)=\displaystyle\int_0^{\infty}y^{q-1}e^{-y}dy=(q-1)\,!\quad\cdots\,\)(8)
ここで、\(\,p=q-1\,\)とすると
\(\quad p\,!=\displaystyle\int_0^{\infty}y^pe^{-y}dy\quad\cdots\,\)(9)
\(\,\,y=ax\,\)とすると\(\,dy=a\,dx\,\)で、(9)式に代入すると
\(\quad p\,!=\displaystyle\int_0^{\infty}(ax)^pae^{-ax}dx=a^{p+1}\displaystyle\int_0^{\infty}x^pe^{-ax}dx\quad\cdots\,\)(10)
よって
\(\quad\displaystyle\int_0^{\infty}x^pe^{-ax}dx=\dfrac{p\,!}{a^{p+1}}\quad\cdots\,\)(11)
これを使って(7)式を積分すると
\(\quad\displaystyle\int_0^{\infty}\!\dfrac{x^3}{e^x-1}dx=\displaystyle\int_0^{\infty}\!x^3(e^{-x}+e^{-2x}+\cdots)dx=\dfrac{3!}{1^4}+\dfrac{3!}{2^4}+\cdots\quad\)
ここでゼータ関数より
\(\quad\zeta(4)=\displaystyle\sum_{n=1}^{\infty}\dfrac{1}{n^4}=\dfrac{1}{1^4}+\dfrac{1}{2^4}+\cdots=\dfrac{\pi^4}{90}\quad\cdots\,\)(12)
なので
\(\quad\displaystyle\int_0^{\infty}\dfrac{x^3}{e^x-1}dx=\dfrac{3!}{1^4}+\dfrac{3!}{2^4}+\cdots=3\,!\,\zeta(4)=\dfrac{\pi^4}{15}\quad\cdots\,\)(13)
4.放射エネルギー
全立体角に対する積分は
\(\quad\displaystyle\int\cos\theta\,d\Omega=\displaystyle\int_0^{2\pi}\displaystyle\int_0^{\frac{\pi}{2}}\cos\theta\,\sin\theta\,d\theta\,d\phi=\pi\quad\cdots\,\)(14)
よって黒体の単位面積当たりの放射エネルギー\(\,I\,\)は
\(\quad I=\pi\displaystyle\int B_{\nu}d\nu=\dfrac{2\pi^5k^4}{15c^2h^3}T^4=\sigma T^4\quad\cdots\,\)(15)
ここで、\(\,\sigma\,\)はステファン・ボルツマン係数である
\(\quad\sigma=\dfrac{2\pi^5k^4}{15c^2h^3}=5.67\times 10^{-8}\)W/m\(^2\)K\(^4\quad\cdots\,\)(16)
|
|
|
|
|