1.経緯
放送大学の「物理と化学のための数学演習」という授業のレポートの課題のひとつに「二重振り子」があったので、忘れないようにここにメモっておきます。
2.レポート課題
天井から長さ \(\ell\) の紐で吊るされた質量 \(M\) の錘に、もう一つの同じ長さ \(\ell\) の紐で同じ質量の錘が垂れ下がった、二重振り子の微小振動を考える。この問題は自由度2の連成振動となっている。以下の問いに答えよ。
\(\textbf{[1]}\) それぞれの紐が鉛直線となす角度を \(\theta_1\,,\,\theta_2\,\)とし、近似式、\(\sin\theta\simeq\theta\,\)を用いて、2つの錘の運動方程式を導き、この連成振動の基準座標と基準振動数を求めよ。紐の質量は小さいとして無視する。
\(\textbf{[2]}\) 2つの紐を変形しない同じ質量 \(m\) の棒で置き換えるとどうなるか。棒の重心はその真ん中にあるとする。
※ 2. の問題は、私のやり方が拙かったせいか、解析解が得られませんでした。そこで、1. だけをここにメモります。
3.方程式の導出
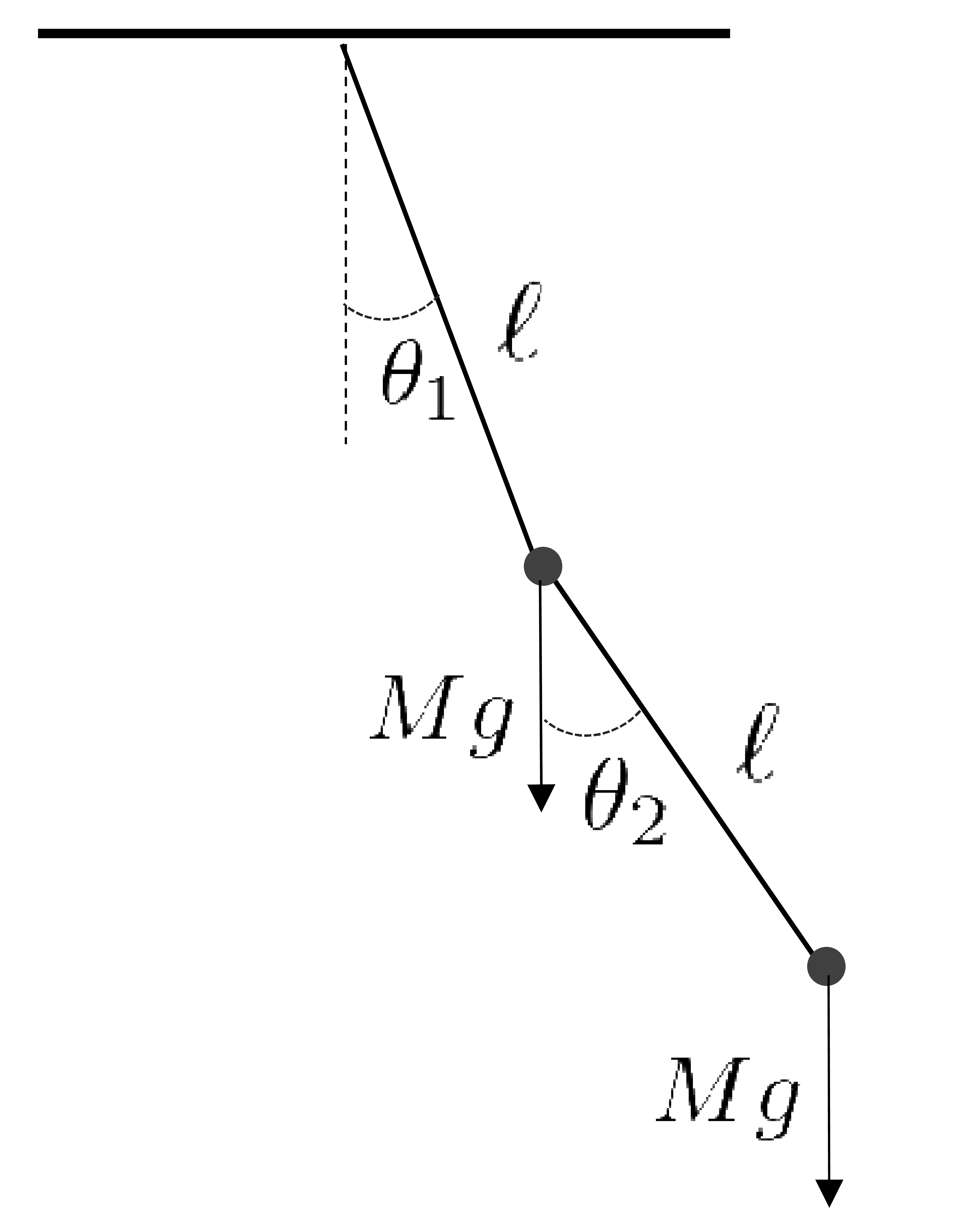 最初のオモリの座標を \((x_1,y_1)\,\) , そこから垂れ下がったオモリの座標を \((x_2,y_2)\,\) とする。
最初のオモリの座標を \((x_1,y_1)\,\) , そこから垂れ下がったオモリの座標を \((x_2,y_2)\,\) とする。
\(x_1=\ell\sin\theta_1\qquad y_1=-\ell\cos\theta_1\)
\(x_2=x_1+\ell\sin\theta_2=\ell(\sin\theta_1+\sin\theta_2)\)
\(y_2=y_1-\ell\cos\theta_2=-\ell(\cos\theta_1+\cos\theta_2)\)
\(\dot{x}_1=\ell\cos\theta_1\dot{\theta}_1\simeq\ell\dot{\theta}_1\)
\(|\dot{x}_1|^2=\ell^2\dot{\theta}_1^2\)
\(\dfrac{1}{2}|\dot{x}_1|^2=\dfrac{\ell^2}{2}\dot{\theta}_1^2\)
\(\dot{x}_2=\ell(\cos\theta_1\dot{\theta}_1+\cos\theta_2\dot{\theta}_2)\simeq\ell(\dot{\theta}_1+\dot{\theta}_2)\)
\(\dfrac{1}{2}|\dot{x}_2|^2=\dfrac{\ell^2}{2}(\dot{\theta}_1+\dot{\theta}_2)^2\)
\(\theta_1\,,\,\theta_2\,\)が小さいとするので、運動エネルギーは \(\quad T=\dfrac{M\ell^2}{2}\dot{\theta}_1^2+\dfrac{M\ell^2}{2}(\dot{\theta}_1+\dot{\theta}_2)^2\)
ポテンシャル・エネルギーは\(\quad U=-Mg\ell(\cos\theta_1+\cos\theta_1+\cos\theta_2)\)
よって、ラグラジアン\(\,L\,\)は
\(L=T-U=\dfrac{M\ell^2}{2}(2\dot{\theta}_1^2+2\dot{\theta}_1\dot{\theta}_2+\dot{\theta}^2)+Mg\ell(2\cos\theta_1+\cos\theta_2)\)
\(\dfrac{\partial L}{\partial\theta_1}\,=-2Mg\ell\sin\theta_1\simeq -2Mg\ell\theta_1\hspace{12mm}\dfrac{\partial L}{\partial\dot{\theta}_1}=M\ell^2(2\dot{\theta}_1+\dot{\theta}_2)\)
\(\dfrac{\partial L}{\partial\theta_2}\,=-Mg\ell\sin\theta_2\simeq -Mg\ell\theta_2\hspace{16mm}\dfrac{\partial L}{\partial\dot{\theta}_2}=M\ell^2(\dot{\theta}_1+\dot{\theta}_2)\)
オイラー・ラグランジュ方程式は\(\quad\dfrac{d}{dt}\left(\dfrac{\partial L}{\partial\dot{q}_1}\right)=\dfrac{\partial L}{\partial q}\,\,\)なので
\(2\ddot{\theta}_1+\ddot{\theta}=-2\dfrac{g}{\ell}\theta_1\qquad \ddot{\theta}_1+\ddot{\theta}_2=-\dfrac{g}{\ell}\theta_2\quad\)の関係が得られる。
これより
\(\left(\begin{array}{@{\,}c@{\,}}\ddot{\theta}_1\\[2pt] \ddot{\theta}_2\end{array}\right)=\dfrac{g}{\ell}\left(\begin{array}{@{\,}rr@{\,}}-2&1\\[2pt]2&-2\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt] \theta_2\end{array}\right)\qquad\)の連立微分方程式が導かれる。
\(\hspace{28mm}\)行列\(\,\,K\,\)
4.方程式の解法
この行列 \(K\) を対角化することで、方程式を解く。まず \(K\) の固有値と固有ベクトルを求める。
固有値 \(\lambda\) は、固有ベクトル \(\textbf{x}\) と \(K\textbf{x}=\lambda\textbf{x}\) の関係にあるので、\(\det{(K-\lambda I)}=0\) より
\(\lambda^2+4\lambda+2=0\qquad \lambda=-2\pm\sqrt{2}\qquad\)が得られる。
\(\textbf{(4-1)} \,\,\lambda_1=-2+\sqrt{2}\) のとき
\(\quad(K-\lambda_1 I)=\left(\begin{array}{@{\,}rr@{\,}}-\sqrt{2}&1\\[2pt]2&-\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}x_1\\[2pt] x_2\end{array}\right)=0\qquad\) より
\(\quad x_1=\dfrac{1}{\sqrt{3}}\qquad x_2=\dfrac{\sqrt{2}}{\sqrt{3}}\qquad\quad \textbf{x}_1=\left(\begin{array}{@{\,}r@{\,}}\frac{1}{\sqrt{3}}\\[2pt]\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\)
\(\textbf{(4-2)} \,\,\lambda_2=-2-\sqrt{2}\) のとき
\(\quad(K-\lambda_2 I)=\left(\begin{array}{@{\,}rr@{\,}}\sqrt{2}&1\\[2pt]2&\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}x_1\\[2pt] x_2\end{array}\right)=0\qquad\) より
\(\quad x_1=\dfrac{1}{\sqrt{3}}\qquad x_2=-\dfrac{\sqrt{2}}{\sqrt{3}}\qquad\quad \textbf{x}_2=\left(\begin{array}{@{\,}r@{\,}}\frac{1}{\sqrt{3}}\\[2pt]-\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\)
5.正則行列の逆行列
固有ベクトルを縦に並べた行列 \(P\) を用いて \(P^{-1}KP\) として \(K\) を対角化する。
\(\quad P=\left(\begin{array}{@{\,}rr@{\,}}\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{3}}\\[3pt]\frac{\sqrt{2}}{\sqrt{3}}&-\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\qquad\quad P^{-1}=\left(\begin{array}{@{\,}rr@{\,}}\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{2\sqrt{2}}\\[3pt]\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2\sqrt{2}}\end{array}\right)\)
この \(P^{-1}\) を用いて、新しい変数 \(\Theta_1\,\,,\,\,\Theta_2\,\,\)を定義する。
\(\quad\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)=P^{-1}\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt]\theta_2\end{array}\right)=\left(\begin{array}{@{\,}rr@{\,}}\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{2\sqrt{2}}\\[3pt]\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2\sqrt{2}}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt]\theta_2\end{array}\right)\)
元の連立微分方程式は、変数 \(\Theta_1\,\,,\,\,\Theta_2$\,\,\)に対する以下の微分方程式と等価である。
\(\quad\dfrac{d}{dt}\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)=\dfrac{g}{\ell}\left(\begin{array}{@{\,}rr@{\,}}-2+\sqrt{2}&0\\[3pt]0&-2-\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)\)
最終的に、運動は2つの固有振動の足し合わせで表され、それぞれの固有振動数 \(\omega_1\,\,,\,\,\omega_2\,\,\)は、
\(\quad\omega_1=\sqrt{2+\sqrt{2}}\sqrt{\dfrac{g}{\ell}}\quad,\quad \omega_1=\sqrt{2-\sqrt{2}}\sqrt{\dfrac{g}{\ell}}\quad\) となる。
|
|
|
|
|
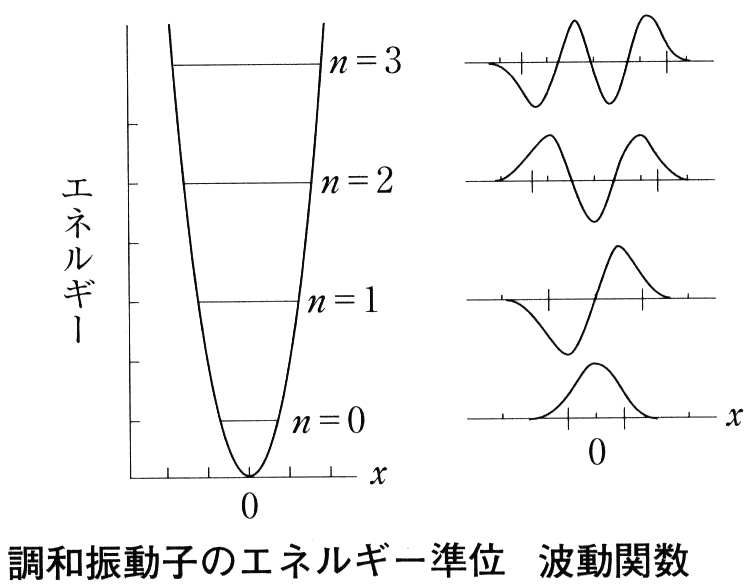 (1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。
(1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。 波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。
波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。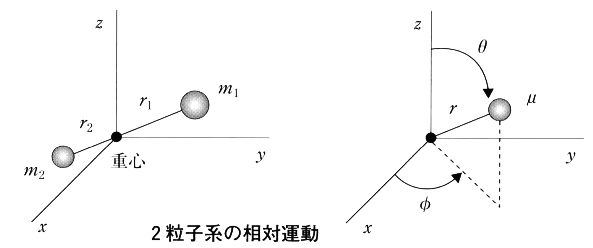 2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。
2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。 直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは
直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは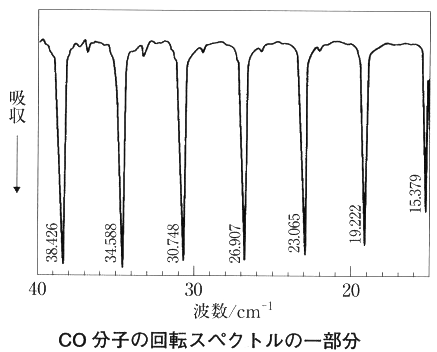 回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。
回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。 このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。
このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。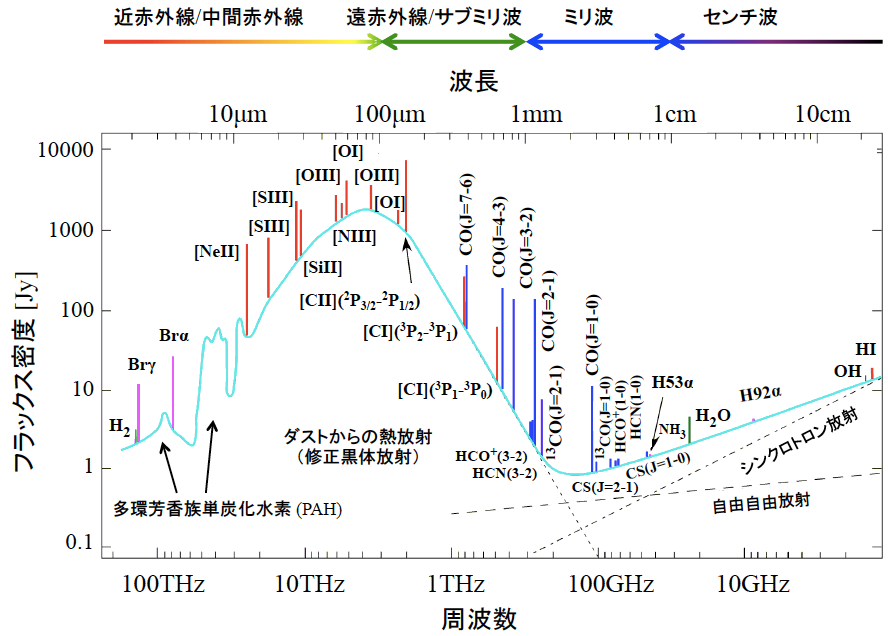
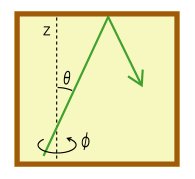
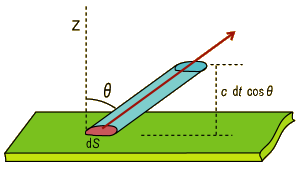 微小面積\(\,dS\,\)から放出される電磁波をイメージする。
微小面積\(\,dS\,\)から放出される電磁波をイメージする。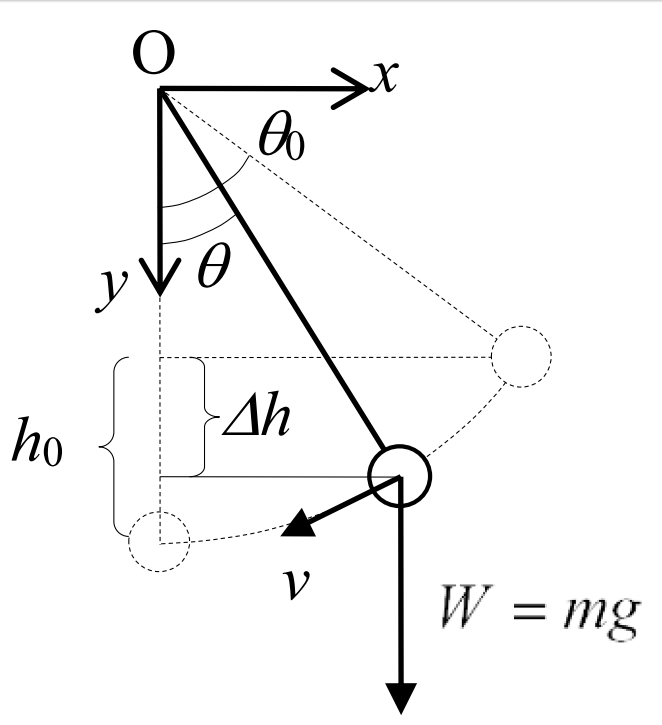 振り子の支点より水平方向に \(\ x\ \)軸をとり、鉛直方向に \(\ y\ \)軸をとると、エネルギー保存則から、次式が成立する
振り子の支点より水平方向に \(\ x\ \)軸をとり、鉛直方向に \(\ y\ \)軸をとると、エネルギー保存則から、次式が成立する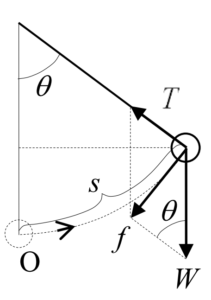
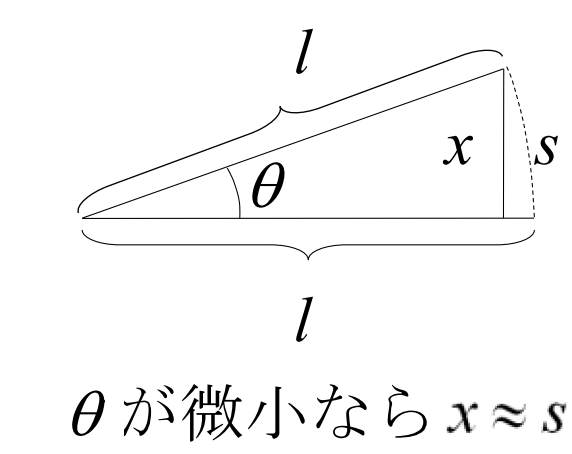 (5)式の運動方程式は、三角関数を含んでいるため、このままでは階を求めることが難しい。但し、円弧の角度\(\ \theta\ \)が微少の場合、三角形の高さ\(\ x=\sin\theta\ \)は円弧の長さ\(\ s\ \)にほぼ等しくなり
(5)式の運動方程式は、三角関数を含んでいるため、このままでは階を求めることが難しい。但し、円弧の角度\(\ \theta\ \)が微少の場合、三角形の高さ\(\ x=\sin\theta\ \)は円弧の長さ\(\ s\ \)にほぼ等しくなり