\(\def\bm{\boldsymbol}\)\(\def\mb{\mathbf}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
音速を流体力学的に導出する。中央大学 棚橋先生の「流体力学」を参考させてもらいました。
1.音波
Wikipediaでは、「気体、液体、固体を問わず、弾性体を伝播するあらゆる弾性波の総称をさす。」となっている。流体として考えると、密度の変化が音速で伝わっていくものということになる。密度が上がると圧力が上がるが、そのために生じる圧力勾配力は流体の圧力を下げる向きにかかるため、密度の値をもとの値に戻そうとする復元力としての役割を果たす。この復元力のために流体の振動が発生するが、これが空間的に伝わっていくのが音波の伝搬である。
1-1: モデル化
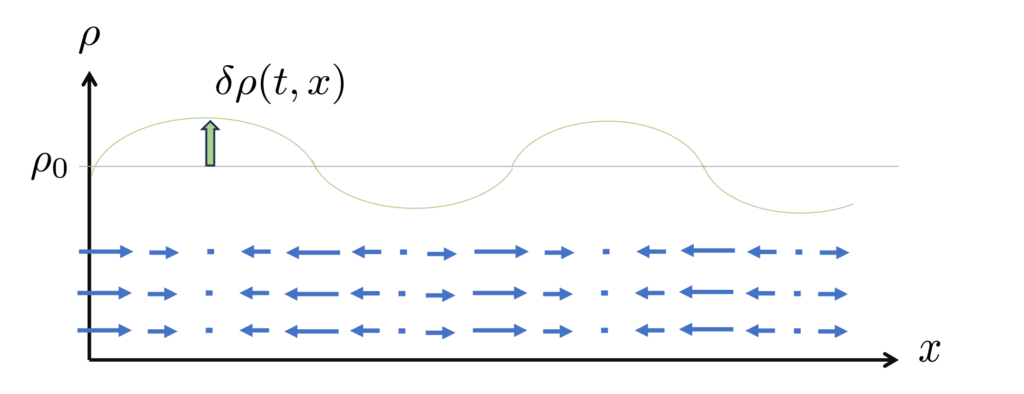 \(x\,\)軸方向に伝搬する平面波の音波について考える。全体の密度は\(\,\rho_0\,\)一定とする。ここで、密度が微小に変化した場合を考える。
\(x\,\)軸方向に伝搬する平面波の音波について考える。全体の密度は\(\,\rho_0\,\)一定とする。ここで、密度が微小に変化した場合を考える。
\(\quad \rho(t,x)=\rho_0+\delta\rho(t,x)\)
\(\qquad\,\,|\delta\rho(t,x)|\ll\rho_0\qquad\cdots\,\)(1)
微小の密度(圧力)変化に対応して、速度場も微小に変化する。音波がない場合は流体は静止しているので、静止速度場はゼロである。
\(\qquad\bm{v}(t,x)=v_0+\delta v(t,x)=\delta v(t,x)\qquad\cdots\,\)(2)
微小圧力変化\(\,\delta\rho(t,x)\,\)とそれに対応する流体の平衡位置からのズレが\(\,\delta v(t,x)\,\)である。
状態方程式を\(\,P=P(\rho)\,\)とする。
1-2: 運動方程式
流体力学の連続の式(質量保存則)とオイラー方程式(粘性を含まない運動量保存則)を適用する。
・連続の式
\(\qquad\pdr{\rho}{t}+\nabla\cdot(\rho\bm{v})=0\qquad\cdots\,\)(3)
\(\qquad\pdr{\rho}{t}+\nabla\cdot(\rho\bm{v})=\pdr{}{t}(\rho_0+\delta\rho)+\nabla\cdot[(\rho_0+\delta\rho)\delta\bm{v}]\)
\(\qquad\quad=\pdr{\delta\rho}{t}+\rho_0\nabla\cdot\delta\bm{v}+\nabla\cdot(\delta\rho\delta\bm{v})\simeq\pdr{\delta\rho}{t}+\rho_0\pdr{\delta v}{x}=0\qquad\cdots\,\)(4)
\(\qquad\quad\delta\rho\delta\bm{v}\,\)項は2次の微少量のため無視した。\(\quad(\quad\because\quad\delta\rho\ll\rho_0\quad)\)
・オイラー方程式
\(\qquad\pdr{\bm{v}}{t}+(\bm{v}\cdot\nabla)\bm{v}=-\dfrac{1}{\rho}\nabla P\qquad\cdots\,\)(5)
まず 左辺は\(\quad\pdr{\delta\bm{v}}{t}+(\delta\bm{v}\cdot\nabla)\delta\bm{v}=\pdr{\delta v}{t}+\pdr{\delta\bm{v}}{x}\delta\bm{v}\sim\pdr{\delta v}{t}\qquad\cdots\,\)(6)
ここで\(\,\partial\bm{v}/\partial t \delta\bm{v}\,\)は2次の微少量なので無視した。
右辺は\(\quad-\dfrac{1}{\rho}\nabla P(\rho)=\dfrac{1}{\rho}\dfrac{dP}{d\rho}\nabla\rho=-\dfrac{1}{\rho_0+\delta\rho}\left.\dfrac{dP}{d\rho}\right|_{\rho_0+\delta\rho}\nabla(\rho_0+\delta\rho)\qquad\cdots\,\)(7)
ここで各項目の計算をまとめる。
\(\qquad\bullet\quad\dfrac{1}{\rho_0+\delta\rho}=\dfrac{1}{\rho_0}\left\{1-\dfrac{\delta\rho}{\rho_0}+\dfrac{1}{2}\left(\dfrac{\delta\rho}{\rho_0}\right)^2-\cdots\right\}\quad\simeq\quad\dfrac{1}{\rho_0}\)
\(\qquad\bullet\quad\left.\dfrac{dP}{d\rho}\right|_{\rho_0+\delta\rho}\sim\left.\dfrac{dP}{d\rho}\right|_{\rho_0}+\left.\dfrac{d^2P}{d\rho^2}\right|_{\rho_0}\delta\rho\quad\simeq\quad\left.\dfrac{dP}{d\rho}\right|_{\rho_0}\)
\(\qquad\bullet\quad\nabla(\rho_0+\delta\rho)\quad\simeq\quad\nabla\delta\rho\qquad(\quad\because\quad\rho_0\sim const.\quad)\)
\(\quad\pdr{\delta v}{t}\,\simeq\,-\dfrac{1}{\rho_0}\dfrac{dP}{d\rho}\nabla\delta\rho=-\dfrac{1}{\rho_0}\dfrac{dP}{d\rho}\pdr{\delta\rho}{x}\qquad\cdots\,\)(8)
\(\blacklozenge\,\,\,\)ここで、(4)式と(8)式を再掲する。
\(\quad\left\{\begin{array}{lr}\pdr{\delta\rho}{t}+\rho_0\pdr{\delta v}{x}=0&\cdots\,\mathrm{(4)}\\
\pdr{\delta v}{t}=-\dfrac{1}{\rho_0}\dfrac{dP}{d\rho}\pdr{\delta\rho}{x}&\cdots\,\mathrm{(8)}\end{array}\right.\)
\(\quad\)ここで、(4)式を時間微分する。
\(\qquad\ppdr{\delta\rho}{t^2}+\rho_0\pdr{}{t}\pdr{\delta v}{x}=\ppdr{\delta\rho}{t^2}+\rho_0\pdr{}{x}\pdr{\delta v}{t}=0\qquad\cdots\,\)(9)
\(\quad\)(9)式に(8)式を代入する。
\(\qquad\ppdr{\delta\rho}{t^2}+\rho_0\pdr{}{x}\left(-\dfrac{1}{\rho_0}\dfrac{dP}{d\rho}\pdr{\delta\rho}{x}\right)=\ppdr{\delta\rho}{t^2}-\dfrac{dP}{d\rho}\ppdr{\delta\rho}{x^2}=0\qquad\cdots\,\)(10)
ここで\(\quad\dfrac{dP}{d\rho}=c^2\quad\)とおくと、式(10)は次のようになる。
\(\qquad\ppdr{\delta\rho}{t^2}=c^2\ppdr{\delta\rho}{x^2}\qquad\cdots\,\)(11)
速度\(\,c\,\)の進行波となる。\(\qquad c=\sqrt{\dfrac{dP}{d\rho}}\)
1-3: 圧縮率で音速を表す
圧縮率\(\,\kappa\,\)とは系にかかる圧力に対して、系の体積がどの程度変化するかを表す状態量であり、以下の式で表される。
\(\qquad\kappa=-\dfrac{1}{V}\dfrac{dV}{dP}\qquad\cdots\,\)(12)\(\hspace{20mm}\)【参考】:個体弾性率\(\,\,\, K=-V\dfrac{dP}{dV}\qquad\)
音速の二乗は
\(\quad c^2=\dfrac{dP}{d\rho}=\dfrac{dV}{d\rho}\dfrac{dP}{dV}\quad\cdots\,\)(13)
ここで\(\quad V=\dfrac{M}{\rho}\quad\)なので、\(\quad \dfrac{dV}{d\rho}=\dfrac{d}{d\rho}\dfrac{M}{\rho}=-\dfrac{M}{\rho^2}=-\dfrac{V^2}{M}\qquad\)これを式(13)に代入すると
\(\qquad\dfrac{dP}{d\rho}=-\dfrac{V^2}{M}\dfrac{dP}{dV}=-\dfrac{V}{\rho}\dfrac{dP}{dV}=\dfrac{1}{\kappa\rho}\qquad\cdots\,\)(14)
よって音速は
\(\qquad c=\sqrt{\dfrac{1}{\kappa\rho}}\qquad\cdots\,\)(15)
1-4: 気体の音速
理想気体で考える。理想気体の状態方程式は、\(\mu\,\)を\(1\)モルの質量として、
\(\qquad P=RT\dfrac{n}{V}=RT\dfrac{M/V}{M/n}=RT\dfrac{\rho}{\mu}\qquad\cdots\,\)(20)
圧力\(\,P\,\)の全微分は
\(\qquad dP=\left(\pdr{P}{T}\right)_{\rho}dT+\left(\pdr{P}{\rho}\right)_Td\rho\qquad\cdots\,\)(21)
\(\qquad\left(\pdr{P}{T}\right)_{\rho}=\dfrac{R\rho}{\mu}=\dfrac{P}{T}\quad,\qquad\left(\pdr{P}{\rho}\right)_T=\dfrac{RT}{\mu}=\dfrac{P}{\mu}\)
これらを式(12)に代入すると
\(\qquad dP=\dfrac{P}{T}dT+\dfrac{P}{\rho}d\rho\qquad\Longrightarrow\quad \dfrac{dP}{P}-\dfrac{d\rho}{\rho}=\dfrac{dT}{T}\qquad\cdots\,\)(22)
\(\blacklozenge\,\,\,\)気体の内部エネルギー\(\,U\,\)は定積比熱より求められる。
\(\qquad dU=C_vdT\qquad\)・単原子分子:\(\,C_v=\dfrac{3}{2}R\qquad\)二原子分子:\(\,C_v=\dfrac{5}{2}R\qquad\cdots\,\)(23)
熱力学の第一法則に」より
\(\qquad dU=-PdV+dQ’\qquad\cdots\,\)(24)
音の振動は断熱的なので\(\,dQ’\,\)をゼロとすると
\(\qquad dU=-PdV=-Pd\dfrac{\mu}{\rho}=P\mu\dfrac{d\rho}{\rho^2}=RT\dfrac{\rho}{\mu}\mu\dfrac{d\rho}{\rho^2}=RT\dfrac{d\rho}{\rho}\qquad\cdots\,\)(25)
\(\blacklozenge\,\,\,\)2原子分子を考え、式(23)と式(25)の係数を比較すると、以下の関係が導かれる。
\(\qquad\dfrac{5}{2}\dfrac{dT}{T}=\dfrac{d\rho}{\rho}\qquad\cdots\,\)(26)
式(26)と式(22)から
\(\qquad\dfrac{dT}{T}=\dfrac{2}{5}\dfrac{d\rho}{\rho}=\dfrac{dP}{P}-\dfrac{d\rho}{\rho}\quad\Longrightarrow\quad\dfrac{dP}{P}=\dfrac{7}{5}\dfrac{d\rho}{\rho}\qquad\cdots\,\)(27)
音速は式(27)と式(20)より
\(\qquad c=\sqrt{\dfrac{dP}{d\rho}}=\sqrt{\dfrac{7}{5}\dfrac{P}{\rho}}=\sqrt{\dfrac{7}{5}\dfrac{RT}{\mu}}\qquad\cdots\,\)(28)
\(\blacklozenge\,\,\,\)空気( 平均分子量:29 温度:0℃ )で計算してみると
\(\qquad\sqrt{\dfrac{7}{5}\dfrac{RT}{\mu}}=\sqrt{\dfrac{7}{5}\dfrac{8.314\times\,273}{29.0\times 10^{-3}}}\simeq 331.0\,\,\)m/s
おおよそ再現出来ている。
◆ 参考資料
- 流体力学 講義ノート 第9回 流体の波動
:https://www2.yukawa.kyoto-u.ac.jp/~norihiro.tanahashi/pdf/hydrodynamics/note_hydrodynamics_9.pdf
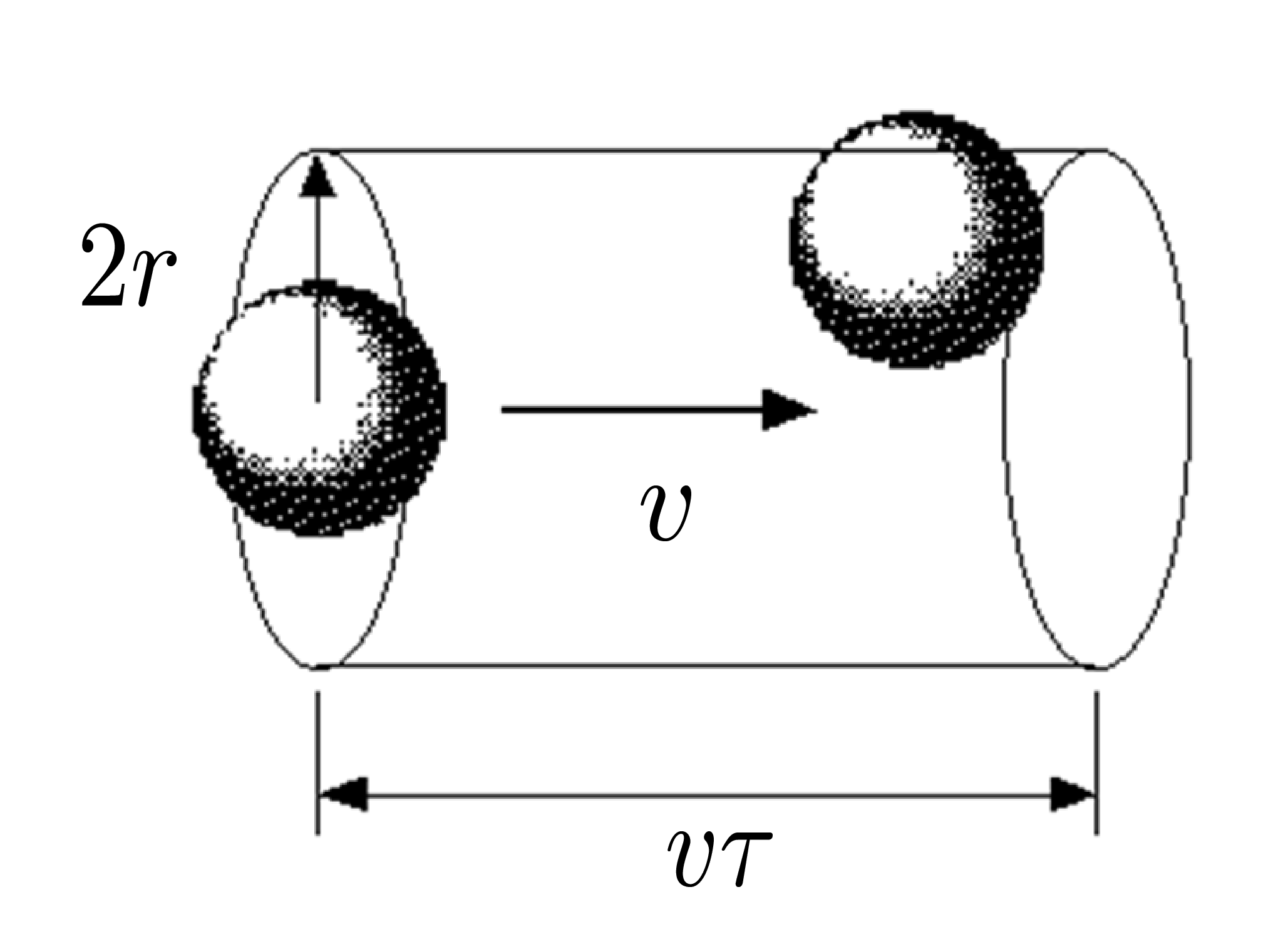 これは速度空間が十分に緩和して、連続体として見なせる状態である。気体を1種類の分子からなっており、半径\(\,r\,\)の剛体球で、ある分子1個が一定の速さ\(\,v\,\)で運動し、他の分子は静止しているという前提で衝突を考える。
これは速度空間が十分に緩和して、連続体として見なせる状態である。気体を1種類の分子からなっており、半径\(\,r\,\)の剛体球で、ある分子1個が一定の速さ\(\,v\,\)で運動し、他の分子は静止しているという前提で衝突を考える。 \(\star\,\)まず、全部の分子が同じ速度で運動している場合を考える。
\(\star\,\)まず、全部の分子が同じ速度で運動している場合を考える。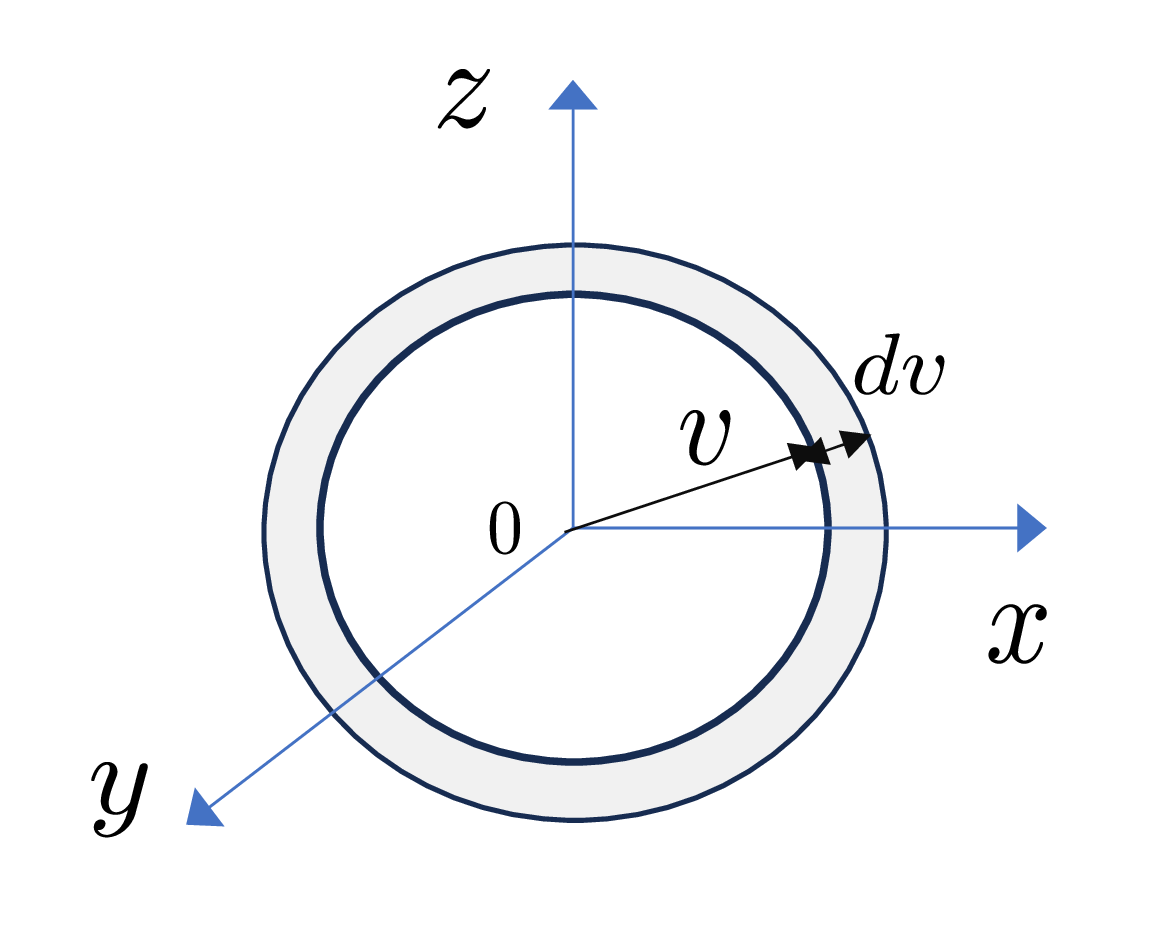 速度空間において、速さが\(\,v\,\)と\(\,v+dv\,\)の間にある分子数を求める。そのためには\(F(v_x,v_y,v_z)dv_xdv_ydv_z\,\)を\(\,v\,\)と\(\,v+dv\,\)の間にある部分について\(\,v_x,v_y,v_z\,\)の積分をする。
速度空間において、速さが\(\,v\,\)と\(\,v+dv\,\)の間にある分子数を求める。そのためには\(F(v_x,v_y,v_z)dv_xdv_ydv_z\,\)を\(\,v\,\)と\(\,v+dv\,\)の間にある部分について\(\,v_x,v_y,v_z\,\)の積分をする。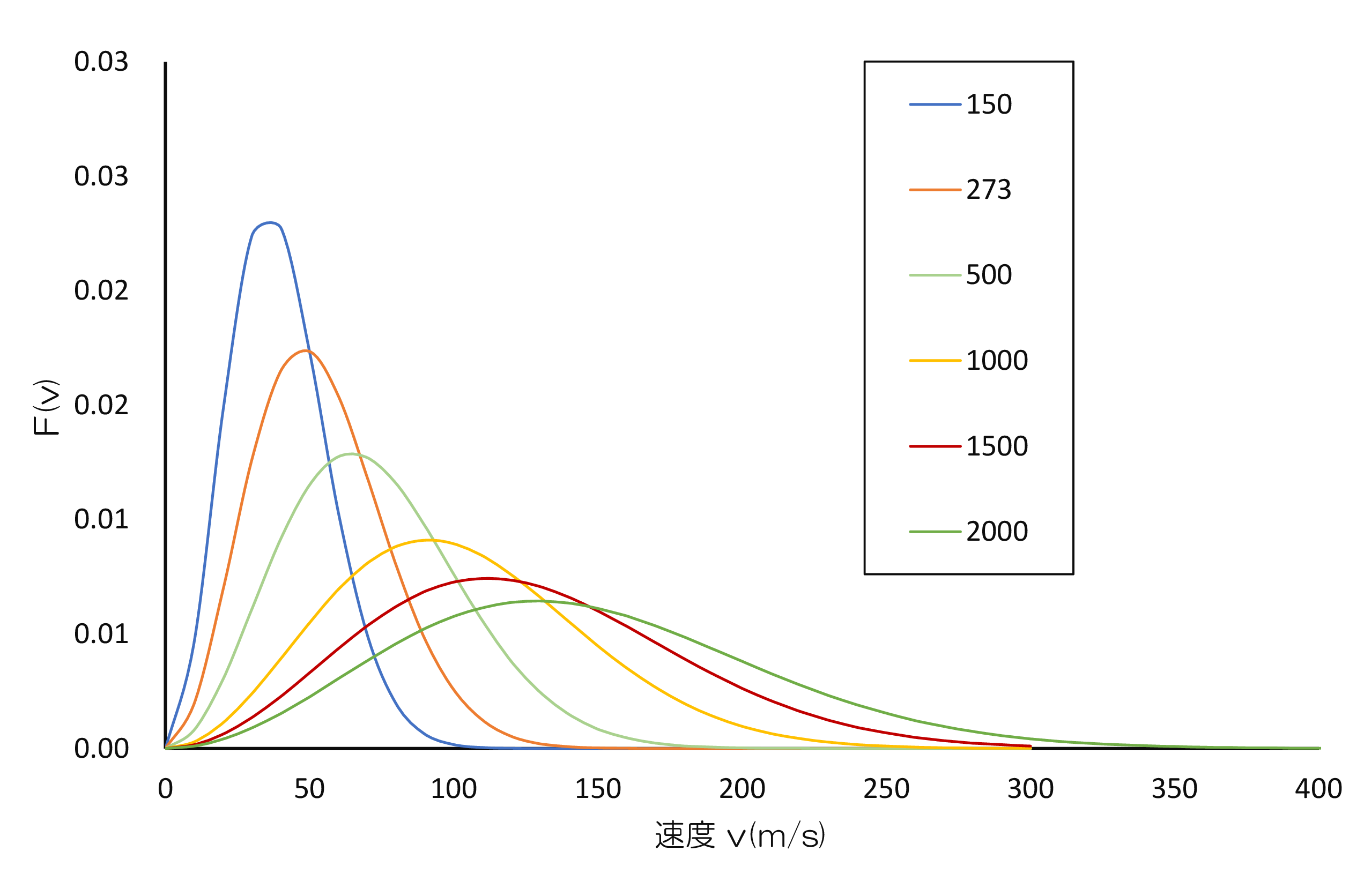
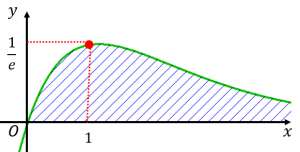 グラフは\(\,y=xe^{-x}\,\)である。\(x\,\to\,\infty\,\)まで積分すると斜線部分の面積は\(\,1\,\)となります。
グラフは\(\,y=xe^{-x}\,\)である。\(x\,\to\,\infty\,\)まで積分すると斜線部分の面積は\(\,1\,\)となります。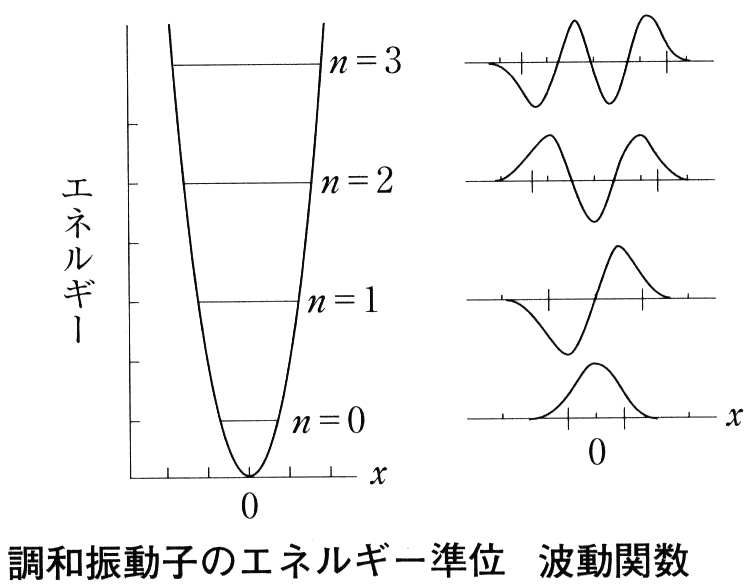 (1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。
(1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。 波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。
波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。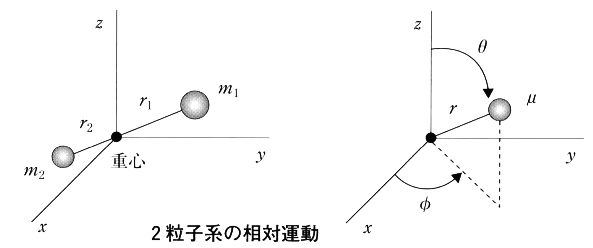 2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。
2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。 直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは
直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは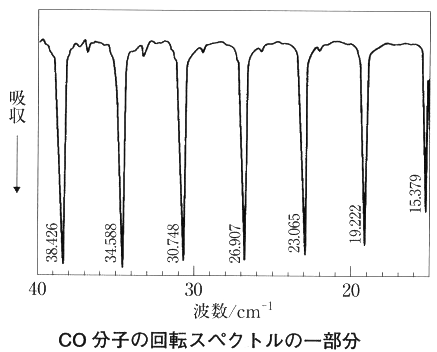 回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。
回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。 このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。
このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。
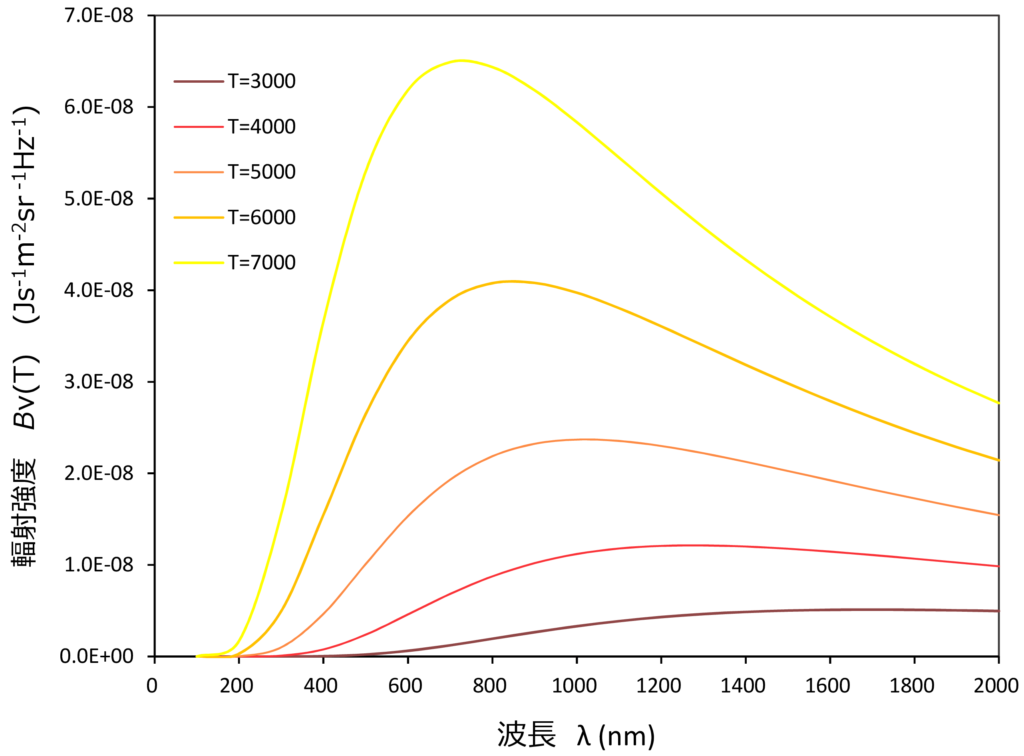
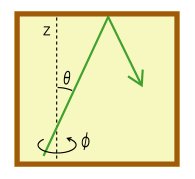
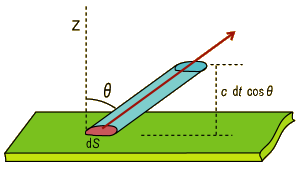 微小面積\(\,dS\,\)から放出される電磁波をイメージする。
微小面積\(\,dS\,\)から放出される電磁波をイメージする。
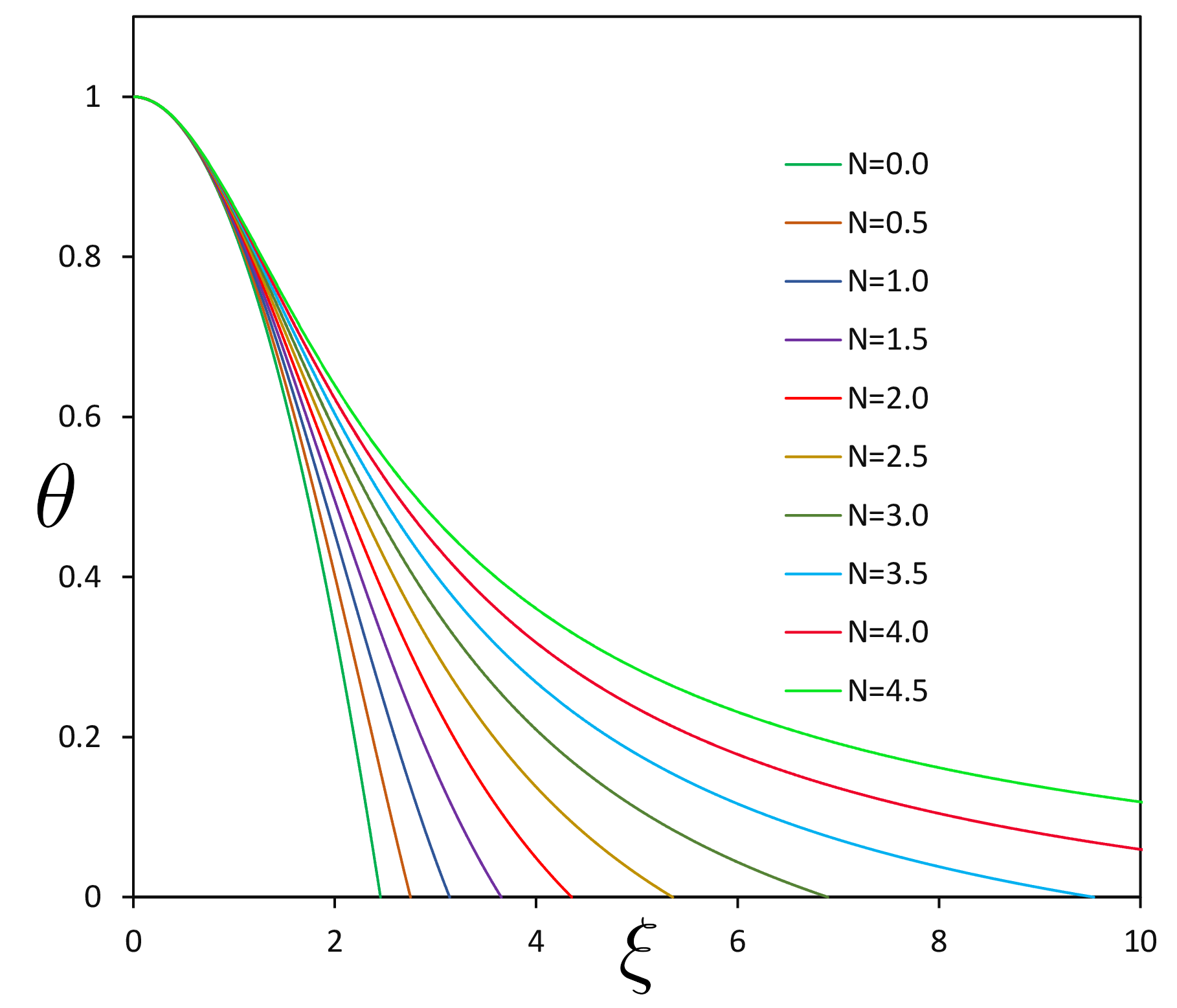
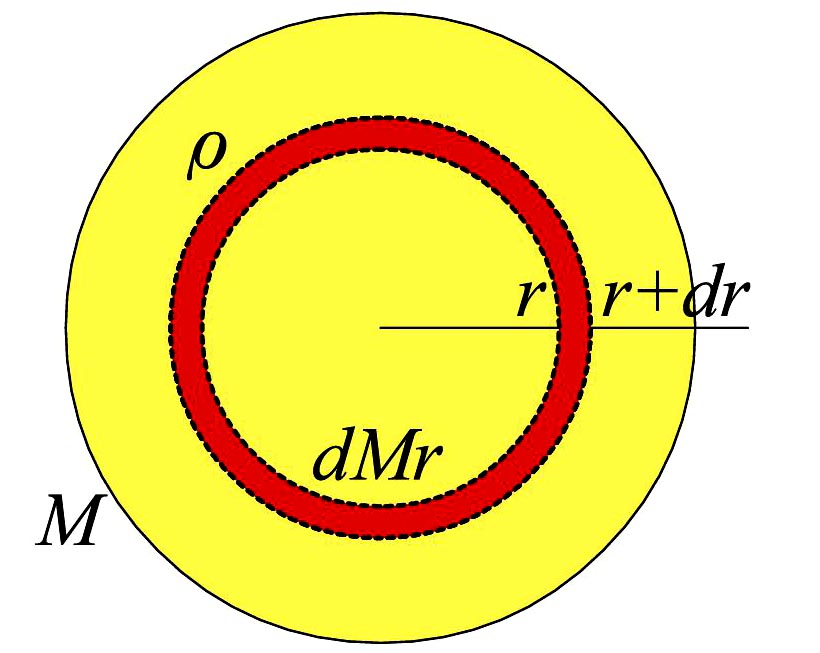 半径\(\,r\,\)、ガス密度は半径の関数とし、\(\,\rho(r)\,\) と表すと、その半径より内側に含まれる質量\(\,M_r\,\)は
半径\(\,r\,\)、ガス密度は半径の関数とし、\(\,\rho(r)\,\) と表すと、その半径より内側に含まれる質量\(\,M_r\,\)は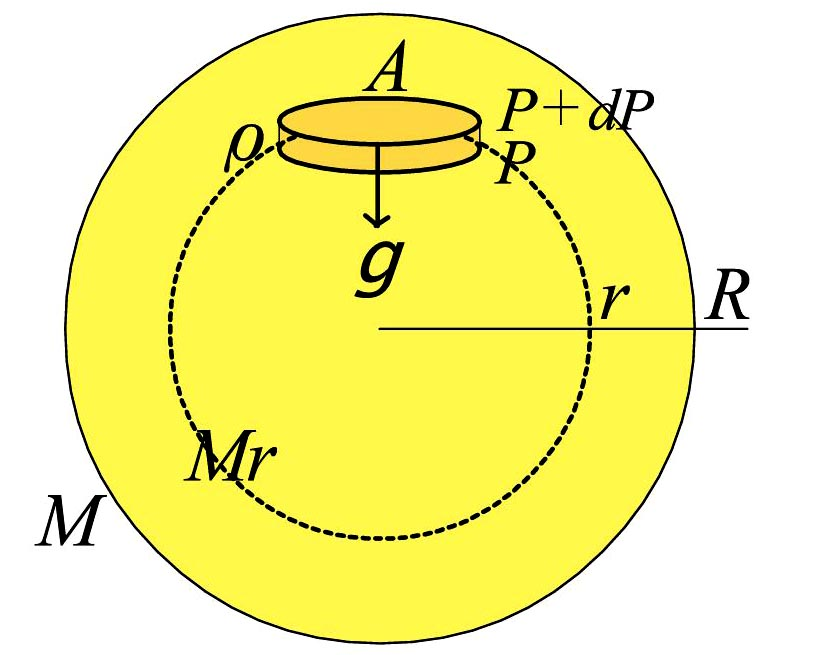 星は自分自身の重力による収縮しようとする力とガス圧による対抗する力がバランスして、力学平衡を保っている。
星は自分自身の重力による収縮しようとする力とガス圧による対抗する力がバランスして、力学平衡を保っている。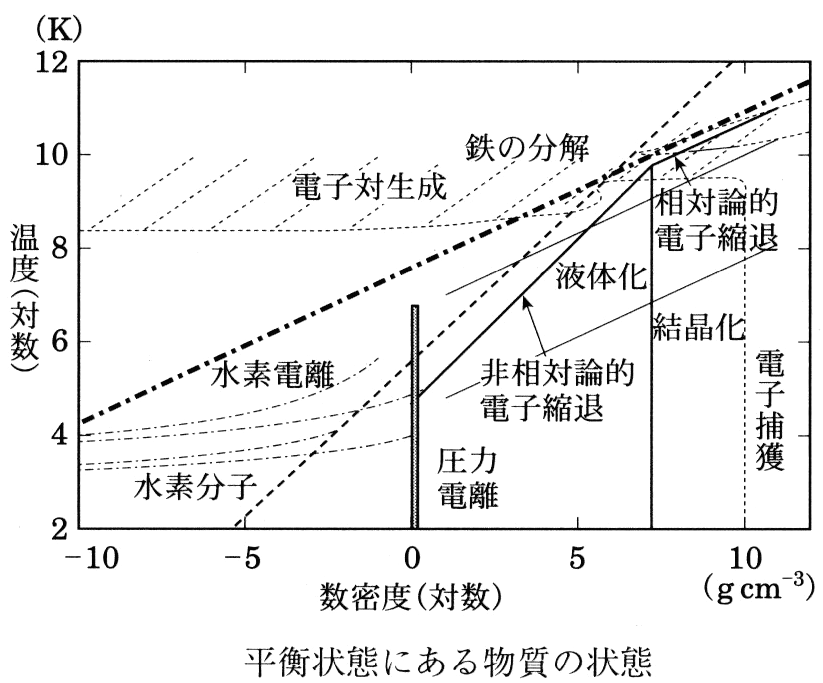
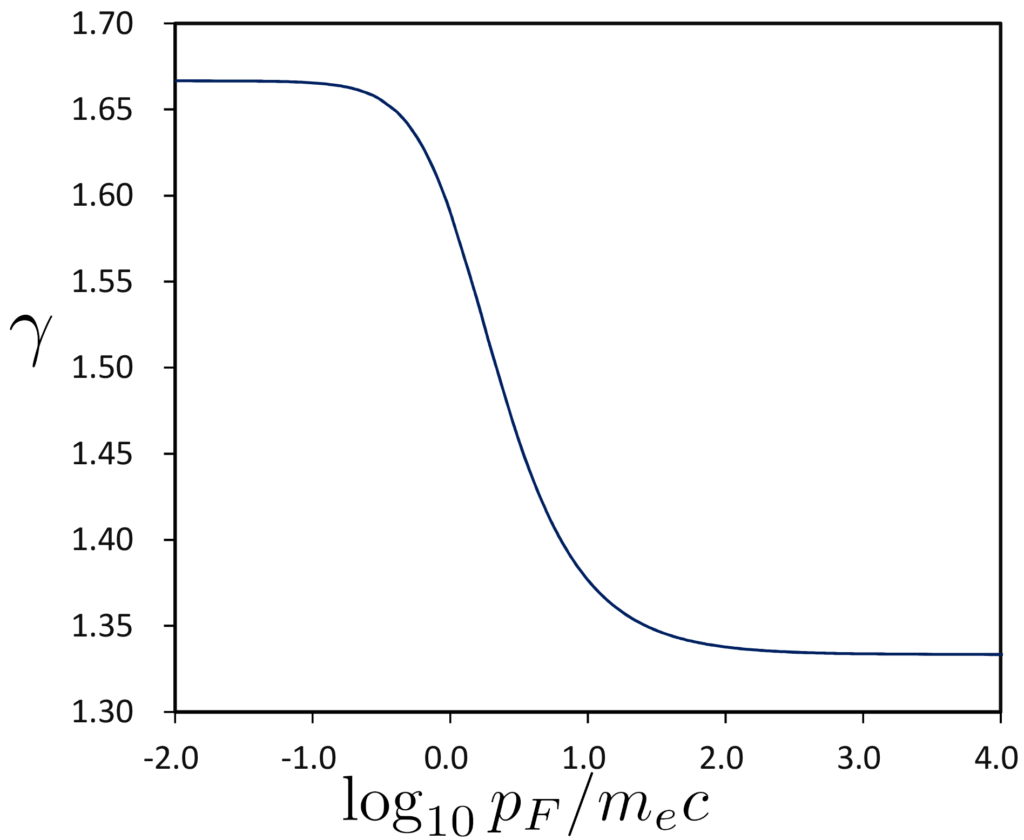
 単原子分子では並進運動の自由度が3なので、\(\,C_V=\frac{3}{2}\mathrm{R}\)。
単原子分子では並進運動の自由度が3なので、\(\,C_V=\frac{3}{2}\mathrm{R}\)。