\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
◆ レイノルズ数 ( Re )
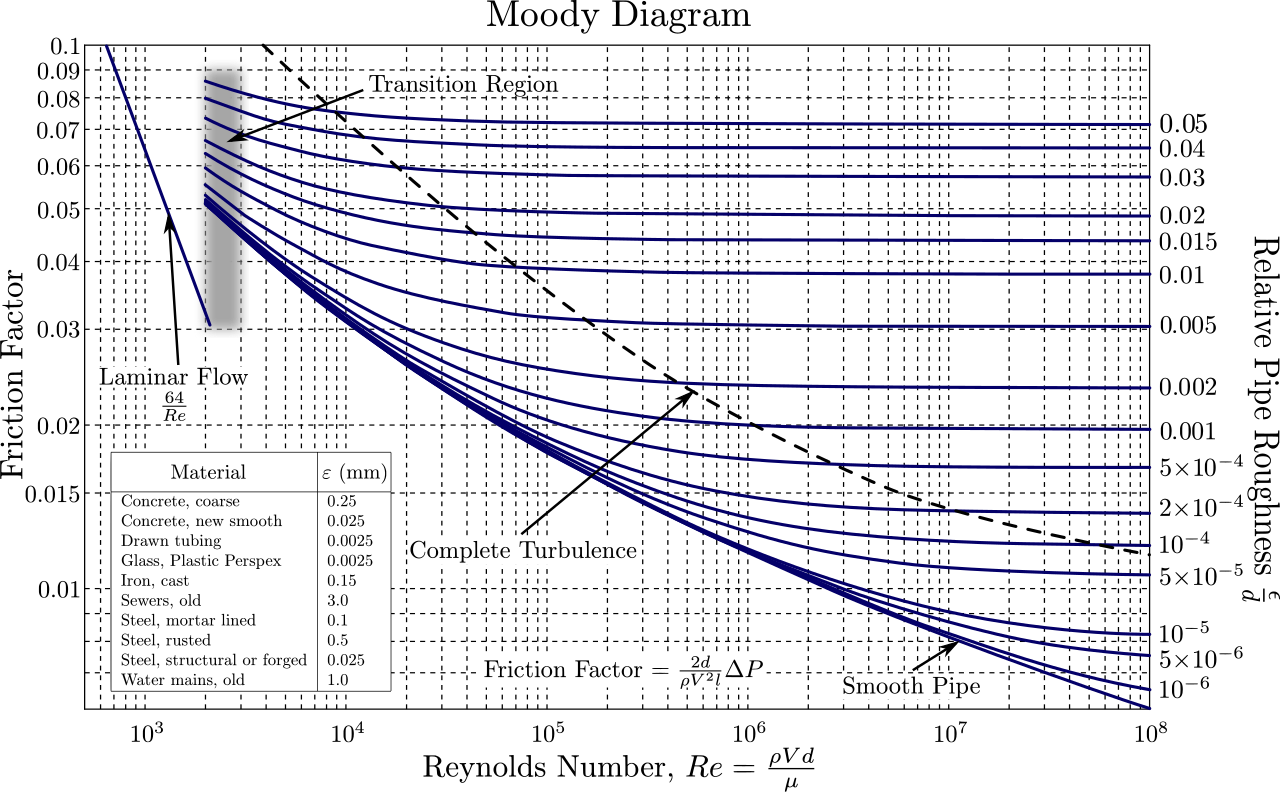
レイノルズ数(Reynolds number)は流体力学において慣性力と粘性力との比で定義される無次元量である。流れの中でのこれら2つの力の相対的な重要性を定量している。
\(\quad\mathrm{Re}=\dfrac{\rho\,U\,L}{\mu}\)
\(\star\)
【例】内径 \(2.5\) cm の配管に水が流れた場合、流速 \(U=0.04\) m/s の時は
\(\quad \mathrm{Re}=\dfrac{1000\times 0.04\times 0.025}{1.01\times 10^{-3}}=1000\quad\)となる。
\(\qquad\)空気の場合、Re=\(1000\) とするには、流速は \(U=0.6\) m/s 必要となる。
\(\quad \mathrm{Re}=\dfrac{1.2\times 0.6\times 0.025}{0.018\times 10^{-3}}=1000\quad\)となる。
◆ プラントル数 ( Pr )
プラントル数( Prandtl number)は熱伝導に関する無次元の物性値であり、熱エネルギー拡散の度合いと運動エネルギー拡散の度合いの比です。プラントル数が大きいほど熱エネルギーの拡散に対して運動エネルギーの拡散の度合いが強いことを意味します。プラントル数は流体に固有の物性値です。流動現象において見られる壁面近傍の境界層を例にすると、プラントル数が \(1.0\) の場合、温度境界層と速度境界層の厚みは等しくなります。プラントル数が \(1.0\) より大きくなると、温度境界層に対して速度境界層の方が厚くなり、プラントル数が \(1.0\) より小さい場合はその逆となります。
\(\quad\mathrm{Pr}=\dfrac{\nu}{\alpha}=\dfrac{\mu\,C_P}{k}\)
\(\star\)
水(\(300\)K \(1\)atm):\(5.466\) 空気(\(300\)K \(1\)atm):\(0.717\) 水銀(\(300\)K \(1\)atm):\(0.025\) 潤滑油(\(300\)K \(1\)atm):\(2040\)
◆ グランホフ数 ( Gr )
グラスホフ数(Grashof Number)は、伝熱現象、物質移動現象に関して、流れ場における粘性力に対する浮力の相対的な影響を示す無次元量である。粘性力と浮力の大きさの比を表した無次元数です。自然対流において流れが層流から乱流に遷移するかどうかを特徴付けます。レイノルズ数が強制対流の流れを特徴付ける無次元数ならば、グラスホフ数は自然対流の流れを特徴付ける無次元数です。グラスホフ数が大きい、つまり浮力の影響が強い場合は、流体はより自由に流れようとするため流動は乱流場となります。一方、グラスホフ数が小さい場合は、流体の粘度による流れの抑制効果が高いため層流場となります。層流と乱流の境界となるグラスホフ数はアプリケーションによって異なりますが、概ね \(10^8\)~\(10^9\) のオーダーです。
\(\quad\mathrm{Gr}=\dfrac{g\beta\Delta\theta L^3}{\nu^2}=\dfrac{g\rho^2\beta\Delta\theta L^3}{\mu^2}\)
\(\star\)
空気で代表温度差:\(100\) K 代表長さ:\(1\) m では \(\mathrm{Gr}=1.466\times 10^{10}\) となる。