\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}\)\(\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}\)
不均等格子を用いて、室内気流の層流解析を行う。河村先生の「流体解析の基礎」を参考にした。
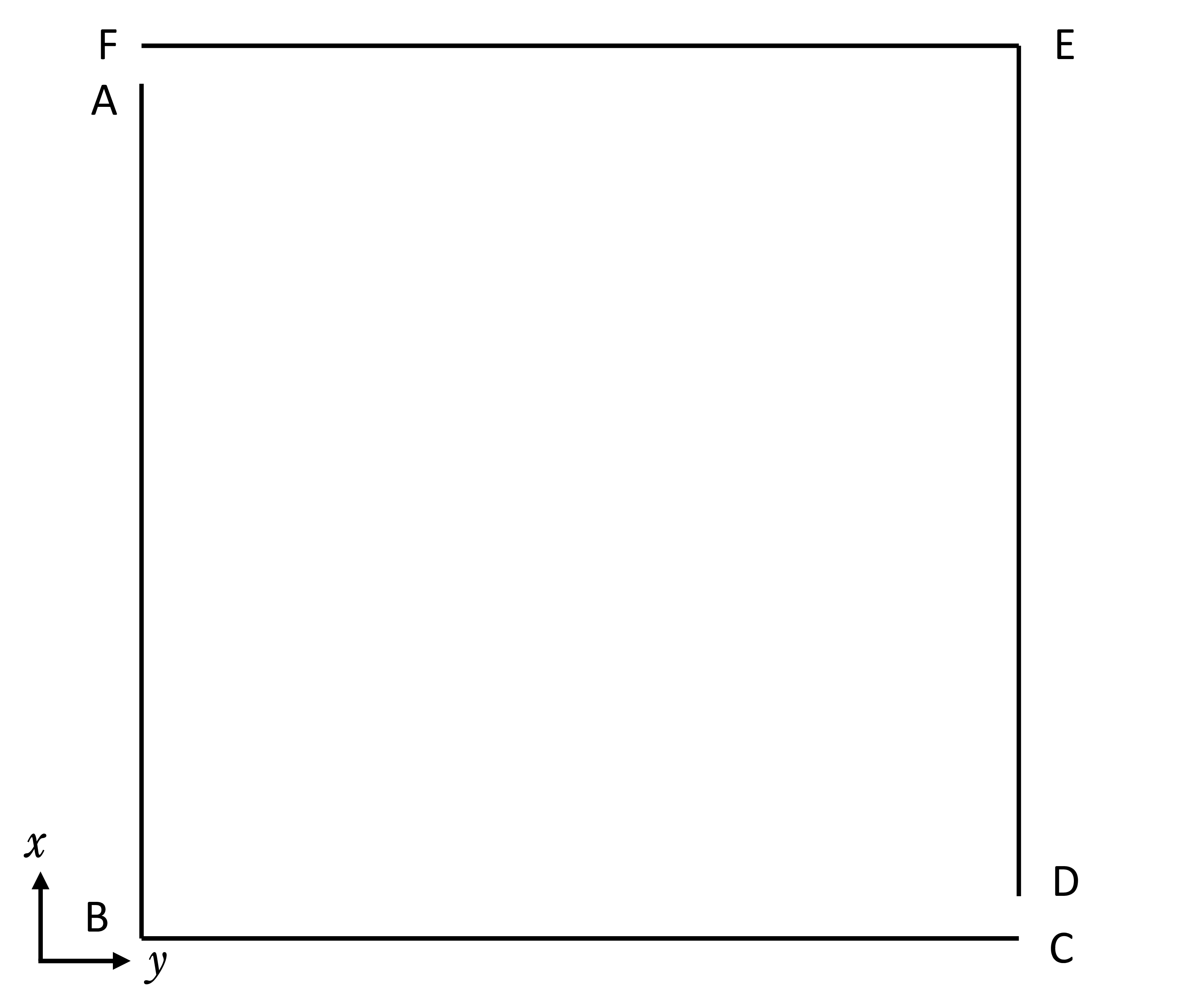
モデルは左の図にしたように、左上に流入口、右下に流失口とする。流れは2次元の層流で、熱の効果は考えないこととする。
ここでは、MAC法を用いる。MAC法の基礎方程式は以下のようになる。
\(\left\{\begin{array}{@{\\,}l}\,\,\Delta p=-\nabla\cdot\{(\bm{V}\cdot\nabla)\bm{V}\}+\dfrac{D^{\,n}}{\Delta t}\quad\cdots\,(1)\\
\,\,\pdr{\bm{V}}{t}+(\bm{V}\cdot\nabla)\bm{V}=-\nabla p+\dfrac{1}{\mathrm{Re}}\Delta\bm{V}\quad\cdots\,(2)\end{array}\right.\)
ここで、\(\,\,D=\nabla\cdot\bm{V}\,\)で、\(\,\,D^{\,n}\,\) は、発散の時間発展を表す。
式(1),(2)の各微分の項を2次元で展開すると
\(\left\{\begin{array}{l}\,\,(\bm{V}\cdot\nabla)\bm{V}=(\,uu_x+vu_y\,,\,uv_x+vv_y\,)\qquad\cdots\,(3)\\
\,\,\nabla\cdot\{(\bm{V}\cdot\nabla)\bm{V}\}=\pdr{}{x}(uu_x+vu_y)+\pdr{}{y}(uv_x+vv_y)=u_x^2+2v_xu_y+v_y^2\quad\cdots\,(4)\\
\,\,D\,\,=u_x+v_y\qquad\cdots\,(5)\\
\,\,\Delta p\,=\,p_{xx}+p_{yy}\qquad\cdots\,(6))\end{array}\right.\)
となるので、式(1)と式(2)は以下のようになる。
\(\left\{\begin{array}{@{\\,}l}\,\,p_{xx}+p_{yy}=-(u_x^2+2v_xu_y+v_y^2)+(u_x+v_y)/\Delta t\quad\cdots\,(10)\\
\,\,u_t+uu_x+vu_y=-p_x+\dfrac{1}{\mathrm{Re}}(u_{xx}+u_{yy})\quad\cdots\,(11)\\
\,\,v_t+uv_x+vv_y=-p_y+\dfrac{1}{\mathrm{Re}}(v_{xx}+v_{yy})\quad\cdots\,(12)\end{array}\right.\)
◆ 不均等格子
小さい流入や流出口の場合、ある程度の格子点を集める必要がある。このような場合は、流出流入口周りに格子点を集めるような不均等格子を用いる。今回は左の図のような格子を使用した。
使用した関数は、式(15)で$\,Z(x)\,$の値を$\,x\,,\,y\,$軸とも使用した。
\(\quad Z(x)=\dfrac{1}{2}\left(1+\dfrac{e^a+1}{e^a-1}\,\dfrac{e^{a(2x-1)}-1}{e^{a(2x-1)}+1}\right)\quad\cdots\,(15)\)
\(\quad a=\log\dfrac{1+b}{1-b}\quad (\,0\,<\,x\,<\,1\,)\)
格子からの差分の計算は別記事を参照の事。
差分の係数\(\,a_1\,,\,a_2\,,\,\cdots\,\)
や\(\quad\,b_1\,,\,b_2\,,\,\cdots\,,c_1\,,\,c_2\,,\,\cdots\,\)も別掲参照。
【１】基礎方程式(10)の差分化は、
\(\quad a_2p_{i-1,j}+b_2p_{i,j}+c_2p_{i+1,j}+a_4p_{i,j-1}+b_4p_{i,j}+c_4p_{i,j+1}\)
\(\qquad\quad =\dfrac{1}{\Delta t}(a_1u_{i-1,j}+b_1u_{i,j}+c_1u_{i+1,j}+a_3v_{i,j-1}+b_3v_{i,j}+c_3v_{i,j+1})\)
\(\qquad\quad -(a_1u_{i-1,j}+b_1u_{i,j}+c_1u_{i+1,j})^2-(a_3v_{i,j-1}+b_3v_{i,j}+c_3v_{i,j+1})^2\)
\(\qquad\quad -2(a_3u_{i,j-1}+b_3u_{i,j}+c_3u_{i,j+1})(a_1v_{i-1,j}+b_1v_{i,j}+c_1v_{i+1,j})\quad\cdots\,(21)\quad\) となる。
【２】(11)(12)式の差分化は以下のようになる。
\(\quad \dfrac{u^{n+1}_{i,j}-u_{i,j}}{\Delta t}+u_{i,j}(a_1u_{i-1,j}+b_1u_{i,j}+c_1u_{i+1,j})+v_{i,j}(a_3u_{i,j-1}+b_3u_{i,j}+c_3u_{i,j+1})\)
\(\qquad\quad =-(a_1p_{i-1,j}+b_1p_{i,j}+c_1p_{i+1,j})\)
\(\qquad\quad +\dfrac{1}{\mathrm{Re}}(a_2u_{i-1,j}+b_2u_{i,j}+c_2u_{i+1,j}+a_4u_{i,j-1}+b_4u_{i,j}+c_4u_{i,j+1})\quad\cdots\,(22)\)
\(\quad \dfrac{v^{n+1}_{i,j}-v_{i,j}}{\Delta t}+u_{i,j}(a_1v_{i-1,j}+b_1v_{i,j}+c_1v_{i+1,j})+v_{i,j}(a_3v_{i,j-1}+b_3v_{i,j}+c_3v_{i,j+1})\)
\(\qquad\quad =-(a_3p_{i-1,j}+b_3p_{i,j}+c_3p_{i+1,j})\)
\(\qquad\quad +\dfrac{1}{\mathrm{Re}}(a_2v_{i-1,j}+b_2v_{i,j}+c_2v_{i+1,j}+a_4v_{i,j-1}+b_4v_{i,j}+c_4v_{i,j+1})\quad\cdots\,(23)\)
【３】 境界条件
入口と出口は\(\,u=1.\,\,,\,v=0.\,\)とする。上下の面は\(\,u=0.\,\,,\,v=0\,\)とし、左右の面は入口と出口以外は\(\,u=0.\,\,,\,v=0\)とする。
# 室内換気 不定形格子(MAC法)
#
import numpy as np
from matplotlib import pyplot as plt
import japanize_matplotlib
import warnings
# 警告非表示
warnings.simplefilter('ignore')
# 条件設定
nx = 31
ny = 31
nxd = nx+1
nyd = ny+1
re = 200 # レイノルズ数
r1 = 1./re
dt = 0.01 # 時間刻み
td = 1./dt
bb = 0.98 # 格子生成パラメータ1
ja = ny-5 # 入り口の格子 No.
jb = 5 # 出口の格子 No
km = 20 # SOR法の最大反復回数
eps = 0.0001 # 繰り返し演算打ち切り誤差
# 配列初期化
a1=np.zeros(nx) # ∂/∂x
b1=np.zeros(nx) # ∂/∂x
c1=np.zeros(nx) # ∂/∂x
a2=np.zeros(nx) # ∂/∂x^2
b2=np.zeros(nx) # ∂/∂x^2
c2=np.zeros(nx) # ∂/∂x^2
a3=np.zeros(ny) # ∂/∂y
b3=np.zeros(ny) # ∂/∂y
c3=np.zeros(ny) # ∂/∂y
a4=np.zeros(ny) # ∂/∂y^2
b4=np.zeros(ny) # ∂/∂y^2
c4=np.zeros(ny) # ∂/∂y^2
u=np.zeros((ny,nx)) # 流速 u
v=np.zeros((ny,nx)) # 流速 v
p=np.zeros((ny,nx)) # 圧力 P
r=np.zeros((ny,nx)) # ポアソン方程式の右辺
# 格子生成
xx=np.zeros(nx)
yy=np.zeros(ny)
x = np.linspace(0, 1, nx)
y = np.linspace(0, 1, ny)
#X, Y =np.meshgrid(x, y)
# 不均等格子形成
ff=(np.exp(bb)+1.)/(np.exp(bb)-1.)
for i in range(nx):
bx=bb*float(i)/float(nx-1)
xq=ff*(np.exp(bx)-1)/(np.exp(bx)+1)
if xq<0:
xq=0.
if xq>1.:
xq=1.
xx[i]=yy[i]=xq
XI, YI =np.meshgrid(xx,yy) # 流速プロット用グリッド
for i in range(1,nx-1): # 不均一格子座標差分情報 X
x1=xx[i+1]-xx[i]
x2=xx[i]-xx[i-1]
x3=xx[i+1]-xx[i-1]
x4=xx[i+1]-2.*xx[i]+xx[i-1]
a1[i]=-x1/(x2*x3)
b1[i]=x4/(x1*x2)
c1[i]=x2/(x1*x3)
a2[i]=2./(x2*x3)
b2[i]=-2./(x1*x2)
c2[i]=2./(x1*x3)
for j in range(1,ny-1): # 不均一格子座標差分情報 Y
y1=yy[j+1]-yy[j]
y2=yy[j]-yy[j-1]
y3=yy[j+1]-yy[j-1]
y4=yy[j+1]-2.*yy[j]+yy[j-1]
a3[j]=-y1/(y2*y3)
b3[j]=y4/(y1*y2)
c3[j]=y2/(y1*y3)
a4[j]=2./(y2*y3)
b4[j]=-2./(y1*y2)
c4[j]=2./(y1*y3)
#
# ----------- 計算ループ ----------------
#
lmax=200 # 繰り返し計算回数
for l in range(1,lmax+1):
# 境界条件
for i in range(nx): # 上下
u[ny-1][i]=v[ny-1][i]=0.
u[0][i]=v[0][i]=0.
for j in range(jb,ny): # 右側
u[j][nx-1]=v[j][nx-1]=0.
for j in range(ja): # 左側
u[j][0]=v[j][0]=0.
for j in range(ja,ny): # 入口
u[j][0]=1.
v[j][0]=0.
for j in range(jb): # 出口
u[j][nx-1]=1.
v[j][nx-1]=0.
# ポアソン方程式の右側の計算
for j in range(1,ny-1):
for i in range(1,nx-1):
u1=a1[i]*u[j][i-1]+b1[i]*u[j][i]+c1[i]*u[j][i+1]
u2=a3[j]*u[j-1][i]+b3[j]*u[j][i]+c3[j]*u[j+1][i]
v1=a1[i]*v[j][i-1]+b1[i]*v[j][i]+c1[i]*v[j][i+1]
v2=a3[j]*v[j-1][i]+b3[j]*v[j][i]+c3[j]*v[j+1][i]
r[j][i]=-u1*u1-2.*u2*v1-v2*v2+td*(u1+v2)
# 収束計算ループ
for k in range(1,km+1):
g2=0.
for j in range(ny): # 圧力の境界条件
p[j][0]=p[j][1]
p[j][nx-1]=p[j][nx-2]
for i in range(nx):
p[0][i]=p[1][i]
p[ny-1][i]=p[ny-2][i]
for j in range(1,ny-1):
for i in range(1,nx-1):
qa=a2[i]*p[j][i-1]+c2[i]*p[j][i+1]
qb=a4[j]*p[j-1][i]+c4[j]*p[j+1][i]
uli=(-qa-qb+r[j][i])/(b2[i]+b4[j])-p[j][i]
g2=g2+uli*uli
p[j][i]=p[j][i]+uli
if g2<eps: break
for j in range(1,ny-1): # Navier Stokes equation の時間発展 u
for i in range(1,nx-1):
u3=u[j][i]*(a1[i]*u[j][i-1]+b1[i]*u[j][i]+c1[i]*u[j][i+1])
u4=v[j][i]*(a3[j]*u[j-1][i]+b3[j]*u[j][i]+c3[j]*u[j+1][i])
u5=a2[i]*u[j][i-1]+b2[i]*u[j][i]+c2[i]*u[j][i+1]
u6=a4[j]*u[j-1][i]+b4[j]*u[j][i]+c4[j]*u[j+1][i]
px=a1[i]*p[j][i-1]+b1[i]*p[j][i]+c1[i]*p[j][i+1]
u[j][i]=u[j][i]+dt*(-u3-u4-px+r1*(u5+u6))
for j in range(1,ny-1): # v の計算
for i in range(1,nx-1):
v3=u[j][i]*(a1[i]*v[j][i-1]+b1[i]*v[j][i]+c1[i]*v[j][i+1])
v4=v[j][i]*(a3[j]*v[j-1][i]+b3[j]*v[j][i]+c3[j]*v[j+1][i])
v5=a2[i]*v[j][i-1]+b2[i]*v[j][i]+c2[i]*v[j][i+1]
v6=a4[j]*v[j-1][i]+b4[j]*v[j][i]+c4[j]*v[j+1][i]
py=a3[j]*p[j-1][i]+b3[j]*p[j][i]+c3[j]*p[j+1][i]
v[j][i]=v[j][i]+dt*(-v3-v4-py+r1*(v5+v6))
if l%40==0 or l==2 or l==4 or l==10:
print("loop= ",l," k=",k," g2=",'{:.3e}'.format(g2))
fig=plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(1, 2, 1)
ax1.set(xlabel='x',ylabel='y')
ax1.set_title('流れ')
ax1.quiver(XI,YI,u,v,color='blue')
ax2 = fig.add_subplot(1, 2, 2)
ax2.set(xlabel='x',ylabel='y')
ax2.set_title('圧力')
ax2.contourf(X,Y,p)
plt.show()
loop= 2 k= 20 g2= 1.727e-01
loop= 4 k= 20 g2= 8.517e-02
loop= 10 k= 20 g2= 1.054e-01
loop= 40 k= 20 g2= 1.263e-03
loop= 80 k= 3 g2= 9.852e-05
loop= 120 k= 1 g2= 9.758e-05
loop= 160 k= 2 g2= 9.333e-05