1. あらゆる物体は光を放っている
電磁波というのは電荷を持った粒子が振動することで発生する。そして電荷を持った粒子は、どこからか飛んできた電磁波を受けると、その影響で振動する。そこらじゅうにある原子は内部に電荷を持っているのだから、何らかの方法で電磁波を放出し、また受け止めていると考えられる。
例えば太陽の光だって電磁波の一種だが、それを受け止めた物体は熱くなる。電磁波の形で遠くから届いたエネルギーが熱に変わるからだ。逆のことも起きている。キャンプファイヤーが終わった後で火を消すと辺りは真っ暗になるが、その真っ暗闇の中で、さっきまで焼かれていた石がぼんやりと赤黒く光っていることがある。そこらにある普通の石が、内部から光を放っているように見えて、少し不気味ではあるが、何だか綺麗だ。
他にも色んな例がある。ストーブの中で焼けた鉄板が赤く光っている。焚き火のときに炭が赤く光っている。ハロゲンヒーターが赤熱している。その光を浴びると、すぐに暖かく感じる。これは間にある空気を伝わって暖められるわけではない。光によって直接暖められるせいだ。このように、熱せられた物体から光や電磁波が出る現象を「熱放射」と呼ぶ。
では物体は何度くらいから光を出し始めるのだろう。実は目に見えないだけで、低い温度の物体でも電磁波を出しているらしい。体温の高い人が近くに来ると直接触らなくても暖かさを感じることがあるだろう。それはその人の体から、可視光線よりも低いエネルギーの光である赤外線が放射されているのだ。
2. ステファン・ボルツマンの法則
では物体は一体どれほどのエネルギーを熱放射の形で放出しているのだろうか?それを調べたのはヨーゼフ・ステファンという 19 世紀の科学者であり、実はあのボルツマンの師である。彼は他の学者たちが過去に行った幾つかの実験結果をまとめた上で、自らも白金の針金に電流を流して赤熱させる実験を行ったりして、熱放射のエネルギー\(\,K\,\)と物体の温度\(\,T\,\)との間に次のような関係があるのではないかという提案を行った。 (1879)
\(\quad K=\sigma T^4\quad\cdots\,\)(1)
この式は「ステファン・ボルツマンの法則」と呼ばれている。なぜボルツマンの名前が入っているかというと、後に、弟子のボルツマンが、当時の最新理論である電磁気学と熱力学を使って、この法則の根拠を説明することに成功したからである。 (1884)
にもかかわらず、この結果はしばらくの間認められることはなかった。多くの科学者がこの実験結果を確認しようとしたが、追試がうまくいかなかったのである。今ではその理由ははっきり分かっているのだが、この法則には少しばかり適用条件があって、当時はそのことがまだ良く分かっていなかったのである。ステファンの実験がうまく行ったのは偶然の幸運であろうと言われている。
3. 理論的導出
電磁波はエネルギーだけでなく運動量をも持つのだということを、電磁気学で学んだ。そこで、こんなことを考えてみよう。容器の壁が温度\(\,T\,\)の物質で出来ていて、そこから放出された電磁波で容器の中が一様に満たされており、そのエネルギー密度が\(\,u\,\)になっていたとする。
この仮定は次のような考えを根拠にしている。もし容器の壁から内側へ向けて電磁波が放出される一方だとすると、容器内部の電磁場のエネルギーは無限に増える一方となるだろう。しかしそうならないのは、容器の壁は電磁場を放出すると同時に吸収も行っていて、一定の状態で安定しているせいだと考えられる。容器の中の電磁場と容器の壁とは熱平衡に達しているというわけだ。電磁場に対しても、温度という概念が使えるということでもある。というわけで、\(\,u\,\)は\(\,T\,\)の関数だと言えるだろう。
さて、そのときの運動量密度\(\,w\,\)と\(\,u\,\)の間には\(\,u=cw\,\)という関係がある。
4. 電磁波のエネルギー密度
マックスウェルの方程式から次の波動方程式が導かれる
\(\quad\nabla^2\mathbf{B}-\dfrac{1}{c^2}\dfrac{\partial^2\mathbf{B}}{\partial t^2}=0\qquad\nabla^2\mathbf{E}-\dfrac{1}{c^2}\dfrac{\partial^2\mathbf{E}}{\partial t^2}=0\quad\cdots\,\)(2)
空間に領域Dをとり、その内部で電磁場が荷電粒子系に及ぼす単位体積当たりの力は
\(\quad\mathbf{f}=\rho\mathbf{E}+\mathbf{j}\times\mathbf{B}\quad\cdots\,\)(3)
であるので荷電粒子系の運動方程式は
\(\quad\dfrac{d\mathbf{P}_{\text{粒子}}}{dt}=\displaystyle\int_{\mathrm{D}}\mathbf{f}\,dv\quad\cdots\,\)(4)
となる。\(\mathbf{P}_{\text{粒子}}\,\)は粒子系の全運動量である。
ここで電場についてのガウスの法則と拡張されたアンペールの法則を使って\(\,\mathbf{f}\,\)を表すと
\(\mathbf{f}=\epsilon_0(\nabla\cdot\mathbf{E})\mathbf{E}-\epsilon_0\dfrac{\partial\mathbf{E}}{\partial t}\times\mathbf{B}+\dfrac{1}{\mu_0}(\nabla\times\mathbf{B})\times\mathbf{B}\quad\cdots\,\)(5)
これよりD内の電磁場の運動量は単位体積当たり以下の値を持つ
\(\quad\mathbf{p}_{\text{場}}\equiv\epsilon_0\mathbf{E}\times\mathbf{B}\quad\cdots\,\)(6)
ここで電束密度\(\,\mathbf{D}=\epsilon_0\mathbf{E}\)、磁束密度\(\,\mathbf{B}=\mu_0\mathbf{H}\,\)であり、真空中を伝搬する電磁場の電場\(\,\mathbf{E}\)と磁束密度\(\,\mathbf{B}\)の大きさの間には\(\,|\mathbf{E}|=c|\mathbf{B}|\)なる関係が成立する。
電場の大きさを\(\,E=|\mathbf{E}|\)とすると電磁場のエネルギー密度は
\(\quad u=\dfrac{1}{2}(\mathbf{E}\cdot\mathbf{D}+\mathbf{B}\cdot\mathbf{H})=\dfrac{1}{2}\left(\epsilon_0E^2+\dfrac{E^2}{c^2\mu_0}\right)\)
\(\qquad =\dfrac{1}{2}(\epsilon_0E^2+\epsilon_0E^2)=\epsilon_0E^2\quad\cdots\,\)(7)
一方、運動量密度\(\,w\,\)は
\(\quad w=|\mathbf{D}\times\mathbf{B}|=\epsilon_0E\cdot\dfrac{E}{c}=\dfrac{\epsilon_0E}{c}=\dfrac{u}{c}\quad\cdots\,\)(8)
5. 電磁波による圧力
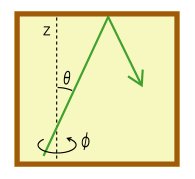
ここで、容器の内部の電磁波を考える。電磁波は容器の壁に当たるたびに壁に運動量を与えるのだから、容器の壁を圧力\(\,p\,\)で押すことだろう。まずは、その\(\,p\,\)と\(\,u\,\)の関係を導く。
説明が簡単に済むように、一辺の長さが\(\,L\,\)の立方体の容器を考えてみる。そしてどの壁を考えても同じことではあるのだが、極座標の積分計算を分かりやすくする都合で、\(\,z\,\)軸の正の方向にある壁に与える圧力を考える。
容器内の全ての電磁波が一つの方向を向いているとする。その全運動量\(\,P\,\)は運動量密度\(\,w\,\)と体積\(\,V=L^3\,\)を掛けて、\(P=wL^3\,\)と表せる。
全ての電磁波の向かう一つの方向というのが、\(\,z\,\)軸に対して\(\,\theta\,\)の角度を持った方向だとすると、壁に当たって反射するたびに、合計で\(\,2P\cos\theta\,\)の運動量を与えることになる。
その頻度であるが、電磁波の速度の\(\,z\,\)軸方向成分が\(\,c\,\cos\theta\,\)であり、往復\(\,2L\,\)の距離を進むたびに再び同じ壁に当たるのだから、1秒間に\(\,c\,\cos\theta/2L\,\)回の衝突を行うことになる。
力というのは1 秒あたりの運動量変化のことであり、それを面積\(\,L^2\,\)で割れば圧力\(\,p\,\)が求まることになる。
\(\quad p=2P\cos\theta\times\dfrac{c\,\cos\theta}{2L}\div L^2\)
\(\qquad =2wL^3\cos\theta\times\dfrac{c\cos\theta}{2L^3}\)
\(\qquad =wc\,\cos^2\theta=u\,\cos^2\theta\quad\cdots\,\)(9)
という形になる。しかしこの結果は、全ての電磁波が一つの方向を向いていると仮定した上での話であり、実際にはあらゆる方向を向いているはずだから、全方向について平等に平均をしてやらないといけないだろう。その為には立体角の考えを使えば良さそうだ。自分が半径1の球の中心にいて、周囲をぐるっと見回していると想像してみよう。どの方向も等しいのだから、この球の表面積にわたって今の結果を積分してやればいい。平均を取るためにはそれを表面積\(\,4\pi\,\)で割ってやればいい。
\(\quad p=\dfrac{u}{4\pi}\displaystyle\int_0^{\pi}\cos^2\theta\sin\theta\,d\theta\displaystyle\int_0^{2\pi}d\phi\)
\(\qquad =\dfrac{u}{4\pi}\left[-\dfrac{1}{3}\cos^3\theta\right]_0^{\pi}\times 2\pi\)
\(\qquad =\dfrac{u}{3}\quad\cdots\)(10)
6. 熱力学的考察
可逆過程での内部エネルギー(\(\,U\,\))変化において以下の関係式がある。
\(\quad dU=T\,dS-p\,dV\quad\) これを変形して
\(\quad\left(\dfrac{\partial U}{\partial V}\right)_T=T\left(\dfrac{\partial p}{\partial T}\right)_V-p\quad\cdots\,\)(11)
という式を作ることが出来る。これに\(\,T\,\)一定の条件下で\(\,V\,\)を変化させ、マクスウェルの関係式を当てはめる。電磁波の場合、この左辺はエネルギー密度\(\,u\,\)になる。
圧力\(\,p\,\)に式(10)を代入すると式(11)は
\(\quad u=\dfrac{1}{3}\,T\,\dfrac{du}{dT}-\dfrac{u}{3}\\[4pt]\therefore\,4u=T\,\dfrac{du}{dT}\qquad\dfrac{du}{u}=4\,\dfrac{dT}{T}\\[4pt]\quad\log u=4\log T+C\qquad\therefore\,\,u=aT^4\quad\cdots\text{(12)}\)となり、形の上ではステファン・ボルツマンの法則と同じものが導かれたことになる。
しかし\(\,u\,\)というのは、物体と電磁場とが熱平衡にあるときの電磁場のエネルギー密度を示しているのであって、物体から放出されるエネルギー\(\,K\,\)とは少し違う概念である。
7. 概念の整理
\(\,K\,\)の意味を「物体の単位表面積から単位時間あたりに放出されるエネルギー」だと言えるようにまとめることが出来れば使いやすい法則になりそうである。
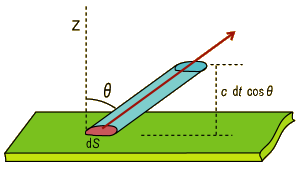 微小面積\(\,dS\,\)から放出される電磁波をイメージする。
微小面積\(\,dS\,\)から放出される電磁波をイメージする。
その微小面の法線方向から\(\,\theta\,\)だけずれた方向へ向かって微小時間\(\,dt\,\)に出て行った電磁波は、図のような筒状体積の内部にあることになるだろう。その体積は\(\,c\,\cos\theta\,dtdS\,\)である。
しかしこの筒状体積とエネルギー密度\(\,u\,\)をかけるだけで、そのエネルギー量が求まるほど単純ではない。なぜなら、このエネルギー密度\(\,u\,\)というのは、あらゆる方向に向かう電磁波が均等に重なり合った合計のエネルギー密度を表しているからである。
今知りたいのは、\(\,\theta\,\)方向へ流れる電磁波のエネルギーだけなのだが、その割合は全方向に向かう電磁波のエネルギーの中でどれくらいあると言えるだろうか。いや、厳密に\(\,\theta\,\)方向に向かう電磁波だけに限定してしまうとそれは無に等しいのである。だからある程度の微小幅を許容して考えないといけない。
こういう時は立体角の考えを使う。半径1の球殻を考え、その表面積の比で表すのである。角度\(\,d\theta\,\)と\(\,d\phi\,\)によって張られる球殻上の微小表面積は\(\,sin\theta\,d\theta\,d\phi\,\)と表されるから、全球殻の面積\(\,4\pi\,\)と比べた割合は\(\,1/4\pi\,\sin\theta\,d\theta\,d\phi\,\)となるだろう。
先ほど考えた筒状領域を、厳密に一方向として考えるのではなく、角度\(\,d\theta\,\)と\(\,d\phi\,\)の微小角度の幅を許してやれば、その範囲を向いている電磁波のエネルギーは
\(\quad\dfrac{1}{4\pi}uc\,\cos\theta\sin\theta\,d\theta\,d\phi\,dt\,dS\quad\cdots\,\)(13)
と表せることになる。この式(13)を微小面より上にある全ての方向について積分してやれば、微小面\(\,dS\,\)から微小時間\(\,dt\,\)内にあらゆる方向へ出て行くエネルギーを表せる。
\(\quad\dfrac{1}{4\pi}uc\,dt\,dS\displaystyle\int_0^{\pi/2}\cos\theta\sin\theta\,d\theta\displaystyle\int_0^{2\pi}d\phi\\[3pt]\qquad=\dfrac{1}{2}uc\,dt\,dS\displaystyle\int_0^{\pi/2}\dfrac{1}{2}\sin 2\theta\,d\theta\\[3pt]\quad =\dfrac{1}{2}uc\,dt\,dS\left[-\dfrac{1}{4}\cos 2\theta\right]_0^{\pi/2}\\[3pt]\quad =\dfrac{1}{4}uc\,dt\,dS\quad\cdots\,\text{(14)}\)
意味を考えれば今計算したのは\(\,K\,dt\,dS\,\)のことでもある。つまり\(\,K\,\)というのは、
\(\quad K=\dfrac{c}{4}u\quad\cdots\,\)(15)
に相当することが言えるのである。ここに先ほどの\(\,u=aT^4\,\)を代入すれば、
\(\quad K=\dfrac{ca}{4}\,T^4=\,\sigma T^4\quad\cdots\,\)(16)
という形が成り立っていることが言えるのである。普通はステファン・ボルツマンの法則と言えば、ここで使ったような意味での\(\,K\,\)と温度\(\,T\,\)の関係のことであり、「ステファン・ボルツマンの定数」として良く知られた\(\,\sigma\,\)もその意味に合うような数値が書かれていることが多い。
|
|
|
|
|
ステファンボルツマンの法則は全波長領域で積分されてますが、測定できる赤外線は一部の波長領域でもステファンボルツマンの法則に適用できるのはなぜでしょうか。
この項目はEMANの物理
https://eman-physics.net/statistic/stefan.html
の記事を参考にしています。
熱平衡状態を仮定しているので、赤外線とかの特定の波長では、成り立たないのではないかと思うのですが(物理屋でないのではっきりとは言えませんが...)