レーン=エムデン方程式は以下の形で表される
\(\quad\dfrac{1}{\xi^2}\dfrac{d}{d\xi}\left(\xi^2\dfrac{d\theta}{d\xi}\right)=-\theta^N\qquad\cdots\,\)(1)
境界条件は、\(\xi\to 0\,\)のとき\(\,\theta=1\,,\,\dfrac{d\theta}{d\xi}=0\,\)である。
[1]中心近傍での扱い
この方程式は\(\xi=0\,\)が確定特異点になっている。この場合、特異点近傍でローラン級数展開を考える。\(\xi=0\,\)の周りの形式解を以下のようにする。
\(\quad\theta(\xi)=1+a_2\xi^2+a_4\xi^4+\cdots\qquad\)(2)
式(2)を式(1)の左辺に代入する。まず、\(\xi\,\)で微分すると
\(\quad\dfrac{d\theta}{d\xi}=2a_2\xi+4a_4\xi^3+\cdots\qquad\)(3)
さらに\(\xi^2\,\)をかけて微分すると
\(\quad\dfrac{d}{d\xi}\left(\xi^2\dfrac{d\theta}{d\xi}\right)=6a_2\xi^2+20a_4\xi^4+\cdots\qquad\)(4)
\(\therefore\,\,\)左辺\(\,\,=6a_2+20a_4\xi^2+\cdots\qquad\)(5)
右辺は、まず\(B_2=a_2\xi^2\,,\,B_4=a_4\xi^4\,,\cdots\,\)として、
\(\quad(1+B_2+B_4+\cdots)^N\,\)の展開を考える。
最初の\(\,1\,\)の項は\(\,1^NB_2^0B_4^0\cdots\,\)であるので、
係数は\(\,\dfrac{N!}{N!0!0!\cdots}\,\)となる。
次の項は\(1^{N-1}B_2^1B_4^0\cdots\,\)で、
係数は\(\,\dfrac{N!}{(N-1)!1!0!\cdots}\,\)となり、
次の\(1^{N-1}B_2^0B_4^1B_6^0\cdots\,\)の係数は
\(\,\dfrac{N!}{(N-1)!0!1!0!\cdots}\,\)となる。因って
\(\quad(1+B_2+B_4+\cdots)^N=1+NB_2+NB_4+\cdots\qquad\)(6)
右辺\(\,=-\theta^N=-1-Na_2\xi^2-Na_4\xi^4-\cdots\,\)となるので
\(\,\xi^m\,\)の係数を比較すると
\(\quad 6a_2=-1\,,\qquad 20a_2=-Na_4\qquad\)となり
\(\quad a_2=-\dfrac{1}{6}\,,\qquad a_4=\dfrac{N}{120}\quad\)を得る。
よって中心近傍での解は
\(\quad \theta(\xi)\simeq 1-\dfrac{1}{6}\xi^2+\dfrac{N}{120}\xi^4\quad\cdots\,\)(7)
と表すことが出来る。
[2]数値計算
この方程式は(その2)で求めた解析解以外の解は数値計算に因らざる得ない。
\(\bigstar\,\)常微分方程式の解法
\(\quad\dfrac{dy_i}{dx}=f_i[x,y_i(x)]\quad i=1,2,\dots\quad\)(8)
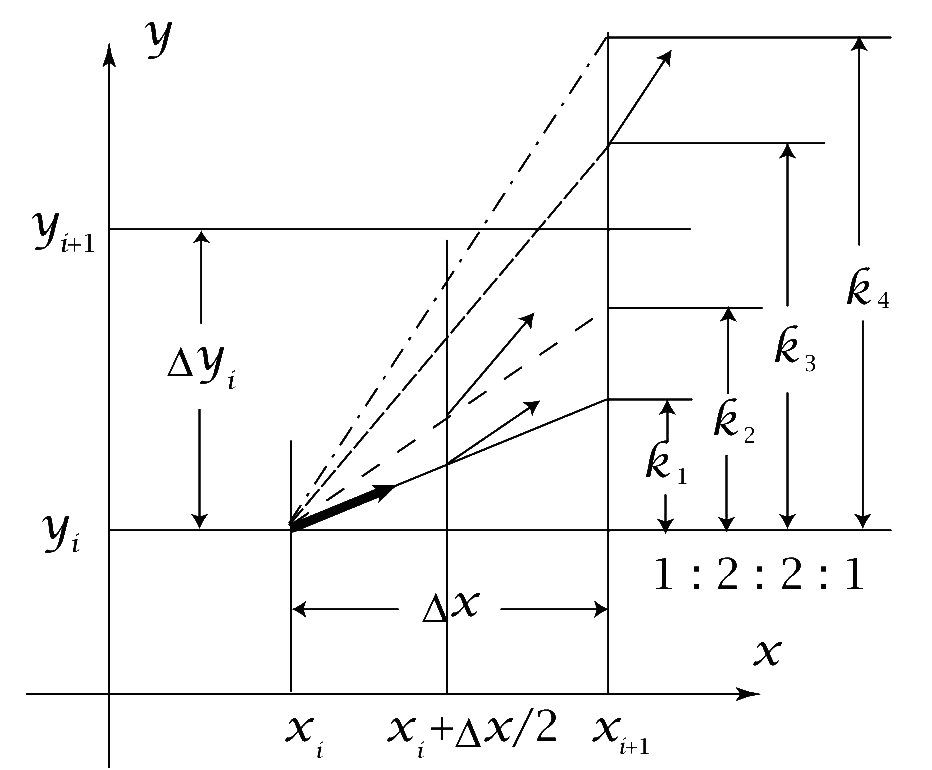
を初期値問題として数値的に解く。
まず、\(x=x_0\,\)において初期値\(\,y_i(x_0)=y_{i0}\,\)が与えられたとき、\(x=x_0+h\,\)での\(\,y_i\,\)の値\(\,y_i(x_0+h)\,\)をもとめ、次のステップでその\(\,(x,y_i)\,\)を新たな初期値として処理を繰り返す。
\(x_0\,\)と\(\,x_0+h\,\)の間の中間の\(\,x\,\)における導関数、\(f(x,y)\,\)の関数値を何回か計算し、それらの適当な平均を用いることによって、高次のTaylor展開を達成するのが Runge-Kutta 法である。
\(\bigstar\,\)Runge-Kutta 法
\(\quad k_1=hf(x_0,y_0)\qquad\qquad\qquad\cdots\,\)(9)
\(\quad k_2=hf(x_0+\frac{h}{2},y_0+\frac{k_1}{2})\qquad\cdots\,\)(10)
\(\quad k_3=hf(x_0+\frac{h}{2},y_0+\frac{k_2}{2})\qquad\cdots\,\)(11)
\(\quad k_4=hf(x_0+h,y_0+k_3)\qquad\cdots\,\)(12)
\(\quad y(x_0+h)=y(x_0)+\frac{1}{6}[K_1+2(K_2+k_3)+k_4]\,\cdots\,\)(13)
まず点(\(\,x_i,y_i\,\))での微係数から\(\,y\,\)の増分\(\,k_1\,\)を推定する(式9)。次に(\(\,x_i,y_i\,\))と今得た点(\(\,x_i+\Delta x,y_i+k_1\,)\)の中間点での微係数から、これに平行な破線で示す直線によって増分\(\,k_2\,\)の推定を行う(式10)。これより第3の推定点\((\,x_i+\Delta x,y_i+k_3\,)\)を得る。第4の推定点まで求めたところで、これら4つの増分推定を\(\,1:2:2:1\,\)の重みを付けて平均化し、これを最終的な増分推定として\(\,y_{i+1}\,\)を求める(式13)。この式は Taylor展開の4次の精度を持つ。
\(\bigstar\,\) 初期値とプログラミング
解くべき式は(1)式だが、\(\xi=x\,,\,\theta=y\,\)と書き換えて見やすくする。
\(\quad\dfrac{1}{x^2}\dfrac{d}{dx}\left(x^2\dfrac{dy}{dx}\right)=-y^N\quad x\!=\!0\quad y\!=\!0\,,\,\dfrac{dy}{dx}=0\,\cdots\,\)(14)
この常微分方程式を連立1階微分方程式に変換する。
\(y1=y\,,\quad y2=x^2\dfrac{dy}{dx}\,\)とおくと
\(\quad \dfrac{dy1}{dx}=\dfrac{y2}{x^2}\qquad\cdots\,\)(15)
\(\quad \dfrac{dy2}{dx}=-x^2y1^N\qquad\cdots\,\)(16)
初期値としては\(\,xi=x=0\,\)でなく、演算の刻み\(\,\xi=x=h\,\)とし、\(y1\,\)は式(7)を使い
\(\quad y1=1-\dfrac{1}{6}h^2+\dfrac{N}{120}h^4\quad\cdots\,\)(17)
\(y2\,\)は、\(\xi^2\dfrac{d\theta}{d\xi}=y2\quad\)としたので
\(\quad y2=h^2\left(-\dfrac{1}{3}h+\dfrac{N}{30}h^3\right)=-\dfrac{1}{3}h^3+\dfrac{N}{120}h^4\quad\cdots\,\)(18)
で設定する。
計算は中心\(\,\,\xi=x=h\,\,\)から始めて、密度係数がゼロ\(\,\,\,\theta=y1=0\,\,\)となる表面までを積分する。また\(\,\,h=1.0\times10^{-6}\,\,\)とした。
[3]数値計算による結果
\(N\,\)を\(0\sim 4.5\,\)まで計算した結果をグラフと表に示す。
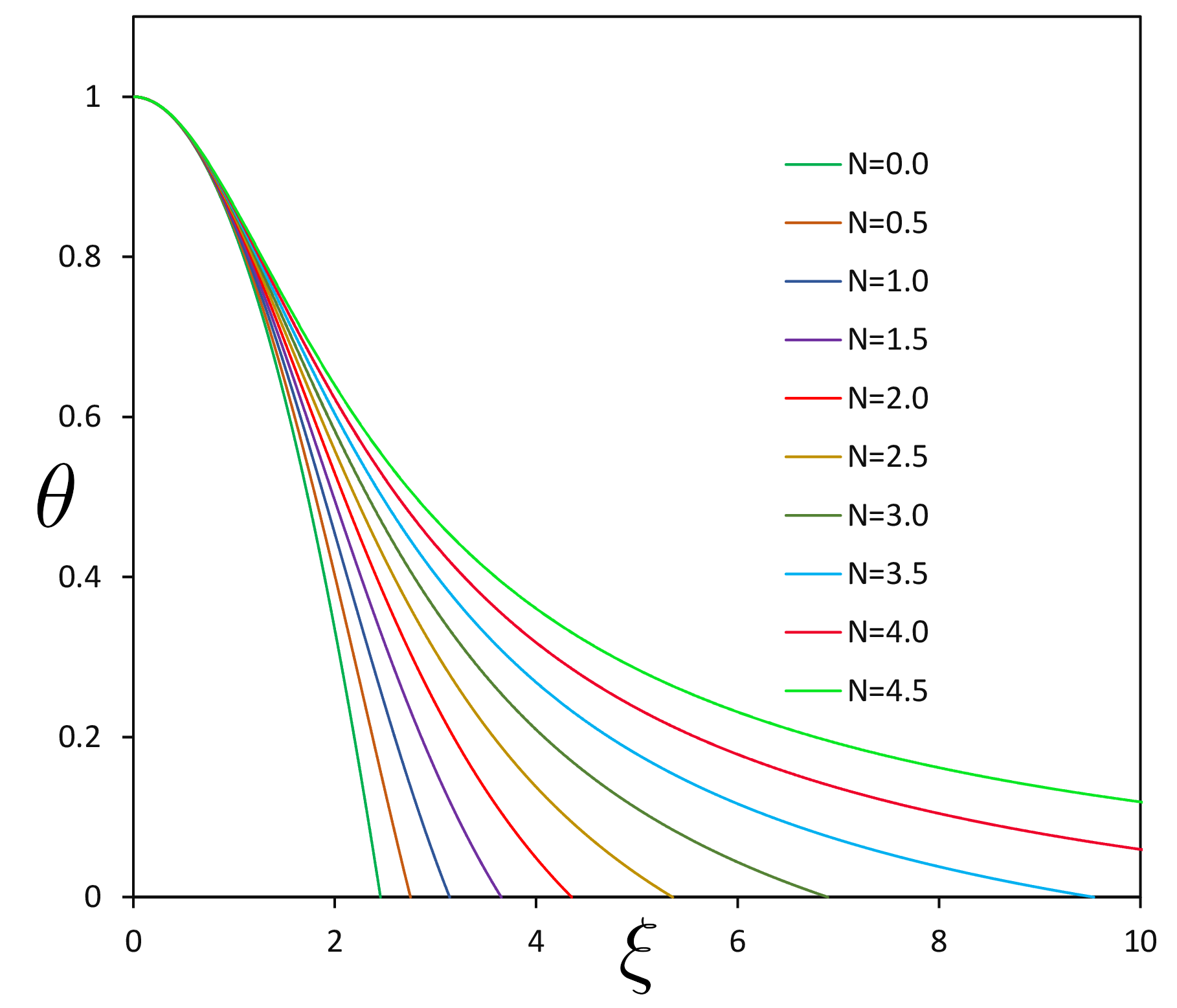
この表は、\(N=n\,\)でガス球の表面(圧力ゼロ\(\,\theta=0\,\))の時の\(\,\xi_n\,\)とそこでの\(\,-1/\xi\,(d\theta/d\xi)\,\)で、中心密度\(\rho_c\,\)を計算するためのパラメータである。
| Nの値 | \(\xi_n\) | \(\left(-\frac{1}{\xi}\frac{d\theta}{d\xi}\right)_{\xi=\xi_n}\) |
| \(0.0\) | \(2.549\) | \(3.291\times10^{-1}\) |
| \(0.5\) | \(2.753\) | \(1.816\times10^{-1}\) |
| \(1.0\) | \(3.142\) | \(1.013\times10^{-1}\) |
| \(1.5\) | \(3.654\) | \(5.564\times10^{-2}\) |
| \(2.0\) | \(4.353\) | \(2.923\times10^{-2}\) |
| \(2.5\) | \(5.355\) | \(1.424\times10^{-2}\) |
| \(3.0\) | \(6.897\) | \(6.152\times10^{-3}\) |
| \(3.5\) | \(9.536\) | \(2.180\times10^{-3}\) |
| \(4.0\) | \(14.972\) | \(5.356\times10^{-4}\) |
| \(4.5\) | \(31.836\) | \(5.386\times10^{-5}\) |
\(\bigstar\,\)結果の見方
\(\xi\,\)は \(\,R=\alpha\xi=\left[\dfrac{(N+1)K}{4\pi G}\rho_c^{\frac{1}{N}-1}\right]^{1/2}\xi\,\cdots\)(21) である。
また中心から\(\,\xi\,\)より内側に含まれる質量\(\,m(\xi)\,\)は
\(\quad m(\xi)=\displaystyle\int_0^{\alpha\xi}4\pi\rho r^2dr\)
\(\qquad\quad =4\pi\alpha^3\rho_c\displaystyle\int_0^{\xi}\xi^2\theta^Nd\xi\)
\(\qquad\quad =-4\pi\alpha^3\rho_c\displaystyle\int_0^{\xi}\dfrac{d}{d\xi}\left(\xi^2\dfrac{d\theta}{d\xi}\right)d\xi\)
\(\qquad\quad =-4\pi\alpha^3\rho_c\xi^2\dfrac{d\theta}{d\xi}\quad\cdots\,\)(22)
で与えられる。したがって星の全質量\(\,M\,\)は
\(\quad M=-4\pi\alpha^3\rho_c\left(\xi^2\dfrac{d\theta}{d\xi}\right)_{\xi=\xi_n}\)
\(\qquad =-4\pi\left[\dfrac{(N+1)K}{4\pi G}\rho_c^{\frac{1}{N}-1}\right]^{3/2}\left(\xi^2\dfrac{d\theta}{d\xi}\right)_{\xi=\xi_n}\,\cdots\,\)(23)
ここで星の平均密度\(\,\bar{\rho}\,\)を考える。
\(\quad\bar{\rho}=\dfrac{M}{4\pi R^3/3}=\dfrac{3M}{4\pi R^3}\)
\(\qquad =-\dfrac{3}{4\pi\alpha^3\xi_n^3}\cdot4\pi\alpha^3\rho_c\left(\xi^2\dfrac{d\theta}{d\xi}\right)_{\xi=\xi_n}\)
\(\qquad =-\dfrac{3}{\xi_n}\rho_c\left(\dfrac{d\theta}{d\xi}\right)_{\xi=\xi_n}\quad\cdots\,\)(24)
\(\bigstar\,\)太陽の場合
これらの関係を太陽の場合で計算してみる。太陽の半径\(\,R=6.960\times10^8\)m 、質量\(\,M=1.9884\times10^{30}\)kg と、恒星の場合に適応できるポリトロープ指数\(\,N=3\,\,(\Gamma=\frac{4}{3}\,)\,\)の計算結果を用いる。
\(\quad\rho_c=\dfrac{M}{4\pi R^3}\left(-\dfrac{1}{\xi}\dfrac{d\theta}{d/xi}\right)_{\xi=\xi_n}^{-1}\quad\cdots\,\)(25)
\(\qquad=\dfrac{1.9884\times10^{30}}{4\pi\cdot (6.960\times10^8)^3\cdot6.152\times10^{-3}}\)
\(\qquad =7.629\times10^4\,\mathrm{kg}\cdot\mathrm{m}^{-3}\)
理科年表によると\(\,\rho_c=1.56\times10^5\,\mathrm{kg}\cdot\mathrm{m}^{-3}\,\)*となっており、計算値は約半分である。まあ、天文のざっくりモデルでの計算としては、まあ合っているといえる。
*[参考]理科年表の太陽の構造の部分
|
|
|
|
|
はじめまして。
今、私はレーンエムデン方程式の数値計算のグラフを出す事に苦戦をしています。
私はPythonで行っているのですが、どのようにグラフを出しましたか?
この時の計算は、Cでプログラミングしました。データをCSV で出力して、Excel に読み込んでグラフ化してます。
教えていただきありがとうございます。