[1]Lane Emden 方程式とは
・宇宙物理学や流体力学において、レーン=エムデン方程式(Lane-Emden equation)は、球対称な密度分布を示す力学平衡にある自己重力流体を記述する微分方程式である。名称は宇宙物理学者のジョナサン・ホーマー・レーンとロバート・エムデンに由来する。
・Jonathan Homer Lane(1819-1880,ニューヨーク州のゲネシー生まれ)エール大学でオルムステッド(Denison Olmsted)に師事し、数学と自然科学を学ぶ。1857 年にワシントン市内に特許事務所を開き、特許関係の顧問や特許弁護士などの業務を始めた。1860 年に南北戦争が勃発すると、ペンシルバニア州北部の兄弟の住む村に移り、冷却用ガス膨張装置を用いた極低温装置の開発や天文学にも興味をもち、ひとりで文献に当たりながら太陽内部構造の研究に思いを深めていた。
・太陽の進化についてはジョン・ハーシェルやケルビン卿の収縮説に興味をもっていたが、内部構造を数学的に扱っていない点がレーンには不満であった。そこで彼は太陽をガス球と仮定し、重力平衡と熱力学過程を基本にして内部構造に関する基本方程式を書き始めた。
「太陽の理論的温度」(Lane,J.H.1870,Amer.J.Sci.&Arts,50,57-74) 自己重力のもとで球状に保たれるガス体の全体的平衡状態を取り扱った歴史的論文である。彼は太陽内部を完全気体と仮定したが、これは大胆な発想であった。完全気体を考えると\(\,p=R\rho T\)、静力学的平衡は\(\,dp=-\dfrac{Gm(r)}{r^2}\rho\,dr\,\)、内部は断熱的に対流平衡となるので、内部構造は\(\,1-\left(\dfrac{\rho}{\rho_c}\right)^{\gamma-1}=\displaystyle\int_0^x\dfrac{\mu(x)}{x^2}dx\,\)にて与えられる。
[2]アウグスト・リターのガス球論
・August Ritter(1826-1908)1853年にゲッチンゲン大学卒業。アーヘン工業大学(現RWTH-Aachen)の構造力学と一般力学の担当教授。「大気の高さに関する考察とガス状天体の内部構造について」ガス球の平衡・振動・安定性の問題に取り組み、自己重力にあるポリトロープガス球の平衡状態についての先駆的研究。
・ポリトロープとは圧力と密度に\(\,pV^n=K\,\) または\(\,p=K\rho^{1+1/n}\,\)の関係を満たす過程のこと。
\(\,T/T_c=y\,,\quad r/a=x\,\)とおいて、重力平衡式と組み合わせると以下の基本微分方程式が得られる。
\(\quad\dfrac{d^2y}{dx^2}+\dfrac{2}{x}\dfrac{dy}{dx}+y^n=0\,\quad\cdots\,\)(1)
この式は ポリトロープガス球の内部構造に関する基本方程式として、エムデンやエディントンに大きな影響を与えた。
[3]エムデンのガス球論
・ロベルト・エムデン(Jacob Robert Emden,1862-1940)スイスの天体物理学および気象学の専門家。1907 年にミュンヘン工科大学の教授。「ガス球論」出版。リターの基本方程式もそのままの形で再度導かれており、通常、エムデンの微分方程式と呼ばれている。リターらと異なり、エムデンはガス球半径を有限の場合と無限の場合を併行して考察している。エムデンの基本的考え方はレーンやリターと変わっていないが、理論が整備され、応用例が多いことからガス球理論の集大成と呼ばれ、4 版を重ねて、星の内部構造論の基本的テキストとなって広く知られるようになった。なお、エムデンの甥、マーチン・シュワルツシルドは 1958 に著書「星の構造と進化」を著わしているが、この書で歴史的なマイルストーンの研究者として、順にエムデン、エディントン、チャンドラセカールの 3 人の名前を挙げている。
[4]星の力学的安定
・連続の式:
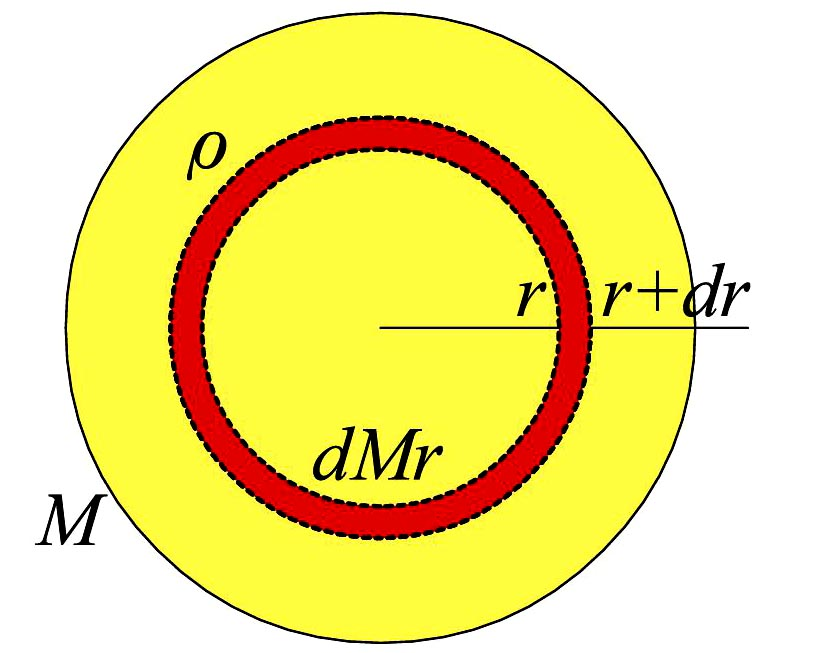 半径\(\,r\,\)、ガス密度は半径の関数とし、\(\,\rho(r)\,\) と表すと、その半径より内側に含まれる質量\(\,M_r\,\)は
半径\(\,r\,\)、ガス密度は半径の関数とし、\(\,\rho(r)\,\) と表すと、その半径より内側に含まれる質量\(\,M_r\,\)は
\(\quad M_r=\displaystyle\int_0^r4\pi r’^2\rho(r)dr’\quad\cdots\,\)(2)
と書くことができる。
この式の両辺を\(\,r\,\)で微分して微分形式で書き表すと
\(\quad\dfrac{dM_r}{dr}=4\pi r^2\rho(r)\quad\cdots\,\)(3)
となる。この式は流体力学の連続の式(continuity equation)の一種である。
・静水圧平衡:
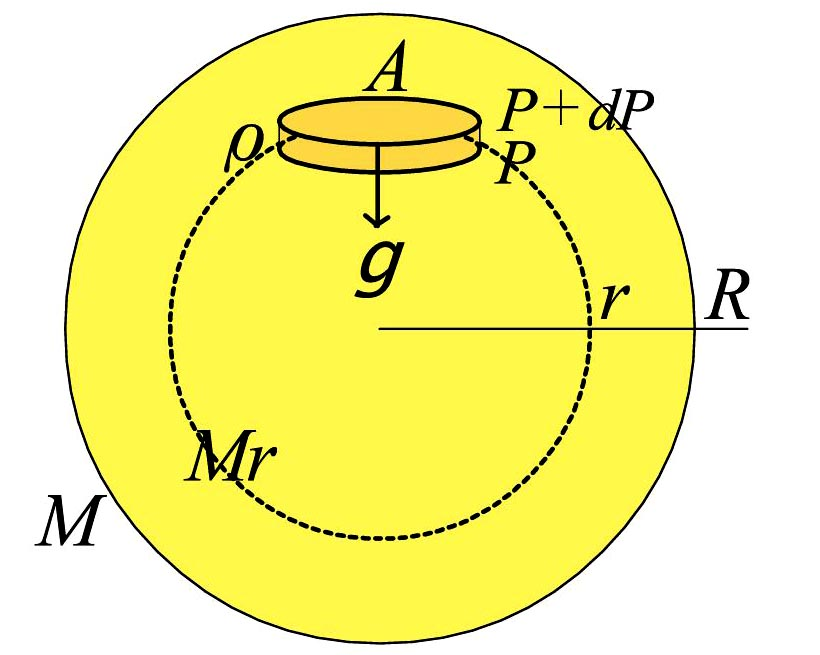 星は自分自身の重力による収縮しようとする力とガス圧による対抗する力がバランスして、力学平衡を保っている。
星は自分自身の重力による収縮しようとする力とガス圧による対抗する力がバランスして、力学平衡を保っている。
\(\,r\,\)を中心からの距離、\(\,P\,\)をそこでの圧力、\(\,G\,\)を重力定数として
\(\quad\dfrac{dP}{dr}=-\dfrac{GM_r}{r^2}\rho\quad\cdots\,\)(4)
と表せる。
連続の式(3)、静水圧平衡の式(4)を解くことで、天体の内部構造を明らかにすることができる。 しかしこの段階では、独立変数が半径\(\,r\,\)で、従属変数は密度\(\,\rho\)、圧力\(\,P\)、質量\(\,M_r\,\)の3つで方程式は2つしかない。ためもうひとつ変数を結びつける式が必要となる。
・ポリトロープ関係
ここで、前出のポリトロープ関係と呼ばれる関係式を導入する。
\(\quad P=K\rho^{1+\frac{1}{N}}\quad\cdots\,\)(5)
\(\,K\,,\,\,N\,\)は定数のパラメータであり、\(\,N\,\)のことをポリトロープ指数と呼ぶ。
[5]レーン=エムデン方程式の導出
天体内部の構造を決めるためには、式(3)、(4)、(5)を解けば良いことになる。まず式(4)から
\(\quad\dfrac{r^2}{\rho}\dfrac{dP}{dr}=-GM_r\quad\cdots\,\)(6)
となり、両辺を\(\,r\,\)で微分すると
\(\quad\dfrac{d}{dr}\left(\dfrac{r^2}{\rho}\dfrac{dP}{dr}\right)=-G\dfrac{dM_r}{dr}\quad\cdots\,\)(7)
となる。これを式(3)に代入すると
\(\quad\dfrac{d}{dr}\left(\dfrac{r^2}{\rho}\dfrac{dP}{dr}\right)=-4\pi Gr^2\rho\quad\cdots\,\)(8)
となる。また、式(5)を\(\,r\,\)で微分すると
\(\quad\dfrac{dP}{dr}=K\left(1+\dfrac{1}{N}\right)\rho^{\frac{1}{N}}\dfrac{d\rho}{dr}\quad\cdots\,\)(9)
が得られる。式(9)を式(8)に代入すると
\(\quad K\left(1+\dfrac{1}{N}\right)\dfrac{d}{dr}\left(r^2\rho^{\frac{1}{N}-1}\dfrac{d\rho}{dr}\right)=-4\pi Gr^2\rho\quad\cdots\,\)(10)
ここで密度\(\,\rho(r)\,\)を星の中心密度\(\,\rho_c\,\)として
\(\quad\rho=\rho_c\theta^N\quad\cdots\,\)(11)
の形で表すこととする。\(\theta\,\)は無次元化した密度。
両辺を\(\,r\,\)で微分すると
\(\quad\dfrac{d\rho}{dr}=\dfrac{d}{dr}\left(\rho_c\theta^N\right)=\rho_cN\theta^{N-1}\dfrac{d\theta}{dr}\quad\cdots\,\)(12)
また、式(11)から以下の関係が導かれる
\(\quad\rho^{\frac{1}{N}-1}=\rho_c^{\frac{1}{N}-1}\,\theta^{1-N}\quad\cdots\,\)(13)
式(10)に式(12)(13)を代入すると
\(\quad K\left(1+\dfrac{1}{N}\right)\dfrac{d}{dr}\left(r^2\rho_c^{\frac{1}{N}-1}\theta^{1-N}\rho_cN\theta^{N-1}\dfrac{d\theta}{dr}\right)\!=\!-4\pi Gr^2\rho_c\theta^N\quad\)
\(\quad\dfrac{K(N+1)\rho_c^{\frac{1}{N}-1}}{4\pi G}\dfrac{1}{r^2}\dfrac{d}{dr}\left(r^2\dfrac{d\theta}{dr}\right)=-\theta^N\quad\cdots\,\)(14)
また式(5)を星の中心にあてはめると
\(\quad P_c=K\rho_c^{1+\frac{1}{N}}\quad\cdots\,\)(15)
この式(15)を式(14)に代入して\(\,K\,\)を消去すると
\(\quad\dfrac{(N+1)P_c}{4\pi G\rho_c^2}\dfrac{1}{r^2}\dfrac{d}{dr}\left(r^2\dfrac{d\theta}{dr}\right)=-\theta^N\quad\cdots\,\)(16)
左辺の係数部分を以下のように定義すると
\(\quad\alpha\equiv\left[\dfrac{(N+1)K}{4\pi G}\rho_c^{\frac{1}{N}-1}\right]^{1/2}\quad\cdots\,\)(17)
\(\quad\dfrac{\alpha^2}{r^2}\dfrac{d}{dr}\left(r^2\dfrac{d\theta}{dr}\right)=-\theta^N\quad\quad\cdots\,\)(18)
ここで、半径を以下の形に無次元化する。
\(\quad\xi=\dfrac{r}{\alpha}\quad\cdots\,\)(19)
これより無次元化した密度\(\,\theta\,\)の\(\,r\,\)の微分は以下のようになる
\(\quad\dfrac{d\theta}{dr}=\dfrac{d\theta}{d\xi}\dfrac{d\xi}{dr}=\dfrac{1}{\alpha}\dfrac{d\theta}{d\xi}\quad\cdots\,\)(20)
微分演算子は以下の形になる
\(\quad\dfrac{d}{dr}=\dfrac{1}{\alpha}\dfrac{d}{d\xi}\quad\cdots\,\)(21)
式(18)にこれらを用いると
\(\quad\dfrac{1}{\xi^2}\dfrac{d}{d\xi}\left(\xi^2\dfrac{d\theta}{d\xi}\right)=-\theta^N\quad\cdots\,\)(22)
この式は無次元化した密度\(\,\theta\)、無次元化した半径\(\,\xi\,\)を結びつけるもので、
レーン=エムデン方程式と呼ばれている。
|
|
|
|
|