エネルギー保存の法則から振り子の周期 \(T\) の式を求める。
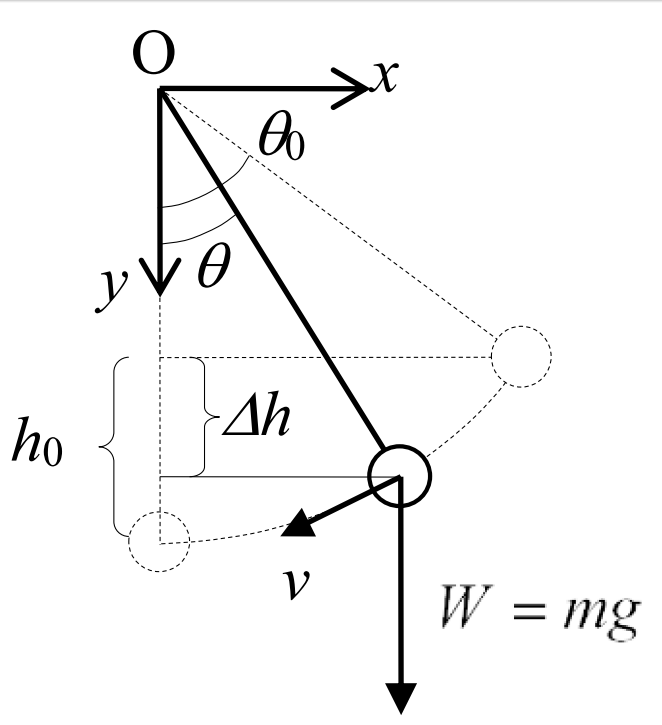振り子の支点より水平方向に \(\ x\ \)軸をとり、鉛直方向に \(\ y\ \)軸をとると、エネルギー保存則から、次式が成立する
\( \dfrac{1}{2}mv^2=mg\Delta h\quad\) (21)
ここで、\(\ v\ \)は重りが円周方向に移動する速度で、\(\Delta h\ \)は重りの落下距離である。ここで
\(\Delta h=l\cos\theta-l\cos\theta_0=l\ (\cos\theta-\cos\theta_0)\quad\) (22)
なので
\( \dfrac{1}{2}mv^2=mgl(\cos\theta-\cos\theta_0)\)
\( \therefore \ v=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\) (23)
さらに
\( v=\dfrac{ds}{dt}=l\dfrac{d\theta}{dt}\quad\) (24)
なので、以下の式が得られる。
\( l\dfrac{d\theta}{dt}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\)(25)
\( dt=\dfrac{1}{\sqrt{2}\omega}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (26)
\(\quad\because\,\,\omega:=\sqrt{\dfrac{g}{l}}\)
この(26)式を積分すると周期を求めることが出来る。積分範囲を4分の1周に相当する \(\ t=T/4\ \)とすると、右辺の積分範囲は\(\ \theta=0\sim\theta_0\ \)となるので、
\( \displaystyle\int_0^{\frac{T}{4}}dt=\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (27)
\(\therefore\,\, T=4\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (28)
この積分を行うために、半角公式を使って以下の変換を行う
\( \cos\theta=1-2\sin^2\frac{\theta}{2}\quad\cos\theta_0=1-2\sin^2\frac{\theta_0}{2}\)
ここで \(\,\,k:=\sin\frac{\theta_0}{2}\quad \sin\phi:=\sin\frac{\theta}{2}/k\,\,\)とすると
\( \cos\theta-\cos\theta_0=1-2\sin^2\frac{\theta}{2}-\left(1-2\sin^2\frac{\theta_0}{2}\right)\)
\(\quad=2\left(\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}\right)=2k^2\cos^2\phi\,\,\)となる
\(k\sin\phi=\sin\frac{\theta}{2}\,\,\)を両辺微分して\(\,\,k\cos\phi\,d\phi=\frac{1}{2}\cos\frac{\theta}{2}\,d\theta\)
\(d\theta=\dfrac{2k\cos\phi\,d\phi}{\cos\frac{\theta}{2}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-\sin^2\frac{\theta}{2}}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\)
なので
\(\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}=\dfrac{1}{\sqrt{2}k\cos\phi}\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\)
\(\quad=\dfrac{\sqrt{2}\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\,\,\)となり、第１種楕円積分の形になる。
 |
 |
 |
 |