「物理の復習」カテゴリーアーカイブ

電荷密度

$\def\bm{\boldsymbol}$$\def\di{\displaystyle}$$\def\ve{\varepsilon}$$\def\vd{\varDelta}$$\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}$$\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}$

1.クーロンの法則

電荷$\,q\,$と$\,Q\,$を持つ２個の点電荷の間の距離を$\,R\,$,それらの間に作用する力の大きさを$\,F\,$と書くと

$F=\dfrac{1}{4\pi\varepsilon_0}\dfrac{q\cdot Q}{R^2}\qquad\cdots\,$(1)

点電荷$\,q\,$の位置ベクトルを$\,\bm{z}_0\,$、$Q\,$を$\,\bm{z}\,$とすると
$R=|\bm{z}_0-\bm{z}|\,$なので、電荷$\,Q\,$が点電荷$\,q\,$に作用する力は

$F(\bm{z}_0)=\dfrac{q}{4\pi\varepsilon_0}\dfrac{Q(\bm{z}_0-\bm{z})}{|\bm{z}_0-\bm{z}|^3}\qquad\cdots\,$(2)

次に、$n\,$個の点電荷$\,Q_1,Q_2,\cdots,Q_n\,$がそれぞれ$\,\bm{z}_1,\bm{z}_2,\cdots,\bm{z}_n\,$
の位置にあるとき、これらが点電荷$\,q\,$に作用する力は、
それぞれの点電荷が作用する力のベクトルの和で与えられる。

$\bm{F}(\bm{z}_0)=\dfrac{q}{4\pi\ve_0}\cdot\di\sum_{i=1}^n\dfrac{Q_i(\bm{z}_0-\bm{z}_i)}{|\bm{z}_0-\bm{z}_i|^3}\qquad\cdots\,$(3)

これがオリジナルのクーロンの法則であるが、$q\,$がゼロの場合、力が働かない事になる。
マックスウェルは近接作用である場の概念を導入し、電場というものを考えた。
これは、電荷がその周りに電場を作り、その電場に電荷が置かれると力が働くと言うことである
つまり、電場$\,\bm{E}\,$(ベクトル量を導入すると (2)式は以下のように分割される。

$\bm{F}(\bm{z}_0)=q\bm{E}(\bm{x}=\bm{z}_0)\quad\cdots\,$(4)$\qquad\bm{E}(\bm{x})=\dfrac{Q}{4\pi\ve_0}\dfrac{\bm{x}-\bm{z}}{|\bm{x}-\bm{z}|^3}\quad\cdots\,$(5)

2.ガウスの法則

(1) 積分形

点電荷$\,Q\,$が閉曲面$\,S\,$に囲まれている。
閉曲面$\,S\,$上にとった微小曲面$\,dS\,$とその上の電磁場$\,\bm{E}(\bm{x})\,$を考える。
$\,dS\,$に立てた単位法線ベクトルを$\,\bm{n}(\bm{x})\,$とすると、
$\bm{E}(\bm{x})\,$の$\,\bm{n}(\bm{x})\,$方向の成分は

$\bm{E}(\bm{x})\cdot\bm{n}(\bm{x})=\dfrac{Q}{4\pi\ve_0R^2}\cos\theta\qquad\cdots\,$(6)

ここで$\,R\,$は点電荷$\,Q\,$から微小面$\,dS\,$までの距離であり、$\theta\,$は$\,\bm{E}(\bm{x})\,$と$\,\bm{n}(\bm{x})\,$
とのなす角である。微小面$\,dS\,$を点電荷$\,Q\,$からみた立体角$\,d\Omega\,$は

$\dfrac{dS\cos\theta}{d\Omega}=\dfrac{R^2}{1^2}\quad$より$\quad d\Omega=\dfrac{\cos\theta\,dS}{R^2}\qquad\cdots\,$(7)

で与えられる。これを式(6)に代入すると$\quad\bm{E}(\bm{x})\cdot\bm{n}(\bm{x})\,dS=\dfrac{Q}{4\pi\ve_0R^2}\cos\theta\,dS=\dfrac{Q}{4\pi\ve_0}d\Omega$
これを閉曲面$\,S\,$上にわたって面積分すると

$\di\int_S\bm{E}(\bm{x})\cdot\bm{n}(\bm{x})\,dS=\dfrac{Q}{4\pi\ve_0}\di\int d\Omega=\dfrac{Q}{4\pi\ve_0}\cdot 4\pi=\dfrac{Q}{\ve_0}\qquad\cdots\,$(8)

点電荷が閉曲面の外側にある場合、$Q\,$からみた同一立体角内に二つの相対する微小曲面$\,dS\,,\,dS’\,$があることになる。
閉曲面の分割は任意であるから$\,dS\ne dS’\,$でよいが、$Q\,$からみた立体角$\,d\Omega\,$が同じなので、相殺される。
$S\,$内に、点電荷$\,Q_1,Q_2,\cdots,Q_n\,$がある場合、全体の電場$\,\bm{E}(\bm{x})\,$の面積分は、
含まれる点電荷の和を$\,\varepsilon_0\,$で割ったものになる。

$\di\int_S\bm{E}(\bm{x})\cdot\bm{n}(\bm{x})\,dS=\dfrac{1}{\ve_0}(Q_1+Q_2+\cdots+Q_n)\qquad\cdots\,$(9)

これを積分型のガウスの法則という。

(2) 微分形

　体積が$\,\varDelta^3x\equiv\varDelta x\varDelta y\varDelta x\,$である立方体の箱を考え
この箱の中に正電荷があるとする。この電荷が作る電場は箱の
中から外向きに出ている。そこで、箱の表面$\,S\,$上の面積分を考える。
まず、$x\,$軸に直交する二つの面 A と B を考える。A 面上では

$\di\int_A\bm{E}\cdot\bm{n}\,dS=E_x(x+\varDelta x,y,z)\varDelta y\varDelta z$
ここで変数$\,y\,,\,z\,$では２次以上の微少量を無視している。B 面上では

$\di\int_A\bm{E}\cdot\bm{n}\,dS=-E_x(x,y,z)\varDelta y\varDelta z$
ここで負号がつくのは、B面上に立てた単位法線ベクトル$\,\bm{n}\,$の方向が$\,x\,$軸の負の
方向を向いているからである。これらを加え合わせると

$\di\int_{A+B}\bm{E}\cdot\bm{n}\,dS=\dfrac{E_x(x+\varDelta x,y,z)-E_x(x,y,z)}{\varDelta x}\cdot\varDelta x\varDelta y\varDelta z=\pdr{E_x(\bm(x)}{x}\varDelta^3 x$

となる。$y\,$軸と$\,z\,$軸に垂直な面についても同様の計算をし、これらを加えると

$\di\int_S\bm{E}\cdot\bm{n}\,dS=\left(\pdr{E_x(\bm{x})}{x}+\pdr{E_y(\bm{x})}{y}+\pdr{E_z(\bm{x})}{z}\right)\varDelta^3x\qquad\cdots\,$(10)

ここで$\,\mathrm{div}\,\bm{E}(\bm{x})\,$という量を定義する。

$\mathrm{div}\,\bm{E}(\bm{x})=\di\lim_{\varDelta^3x\to 0}\dfrac{1}{\varDelta^3 x}\di\int_S\bm{E}\cdot\bm{n}\,dS\qquad\cdots\,$(11)　より

$\mathrm{div}\,\bm{E}(\bm{x})=\pdr{E_x(\bm{x})}{x}+\pdr{E_y(\bm{x})}{y}+\pdr{E_z(\bm{x})}{z}\qquad\cdots\,$(12)

これをベクトル$\,\bm{E}(\bm{x})\,$の発散 (divergence) という。

ここで、閉曲面$\,S\,$によって囲まれる空間の体積を$\,V\,$とすると、ガウスの定理より

$\di\int_S\bm{E}(\bm{x})\cdot\bm{n}\,dS=\di\int_V\mathrm{div}\,\bm{E}(\bm{x})\,d^3x\qquad\cdots\,$(13)

ここで、式(9)の左辺は式(13)のように変形されるから、式(9)は

$\di\int_V\mathrm{div}\,\bm{E}(\bm{x})\,d^3x=\dfrac{1}{\ve_0}\di\int_V\rho(\bm{x})d^3x\quad$となる。

ここで積分領域$\,V\,$を任意の点$\,\bm{x}\,$の周りの微小領域$\,\varDelta^3x\,$にとれば
$\mathrm{div}\,\bm{E}(\bm{x})\varDelta^3x=\rho(\bm{x})\varDelta^3x/\ve_0\,$となり、任意の場所で

$\mathrm{div}\,\bm{E}(\bm{x})=\dfrac{1}{\ve_0}\rho(\bm{x})\qquad\cdots\,$(14)

これを微分形のガウスの法則という。

3.静電ポテンシャル

(1) ストークスの定理

任意のベクトル場を考えたとき、以下の式が成立するのがストークスの定理

$\di\int_C\bm{X}(\bm{x})\cdot d\bm{x}=\di\int_S\mathrm{rot}\,\bm{X}(\bm{x})\cdot\bm{n}(\bm{x})\,dS\qquad\cdots\,$(15)

左辺の線積分は図のような任意の閉曲線$\,C\,$について、
図のような方向への１周にわたる積分であり、右辺の積分は
閉曲線$\,C\,$によって囲まれた任意の曲面$\,S\,$上での面積分である。
また、$\mathrm{rot}\,\bm{X}(\bm{x})\,$とは、その成分が

$\mathrm{rot}\,\bm{X}(\bm{x})\equiv\left(\pdr{X_z}{y}-\pdr{X_y}{z},\,\pdr{X_x}{z}-\pdr{X_z}{x},\,\pdr{X_y}{x}-\pdr{X_x}{y}\right)\quad\cdots\,$(16)

ここで、まず２次元で閉曲面$\,C’\,$を考える。$\bm{X}(\bm{x})\,$を$\,\bm{Y}(x,y)\,$と書き換える。
すると線積分は、２次以上の微少量を無視すると

$\di\int_{C’}\bm{Y}(x,y)\cdot d\bm{x}=Y_x(x,y)\varDelta x+Y_y(x+\vd,y)\vd y+Y_y(x,y)(-\vd y)+Y_x(x,y+\vd y)(-\vd x)$
$\hspace{30mm}=\left(\pdr{Y_y(x,y)}{x}-\pdr{Y_x(x,y)}{y}\right)\vd x\vd y$
$\hspace{30mm}=(\mathrm{rot}\,\bm{Y}(x,y))_z\vd x\vd y\qquad\cdots\,$(17)

式(17)より

$\left(\pdr{Y_y(x,y)}{x}-\pdr{Y_x(x,y)}{y}\right)=\dfrac{1}{\vd x\vd y}\di\int_{C’}\bm{Y}(x,y)\cdot d\bm{x}$
このような線積分を各微小長方形に分割して行う。隣り合わせの線積分の方向が反対向きなので
打ち消し合うことになる。最終的に隣り合う相手のいない周辺上の線積分だけが残るので、

$\di\int_{C’}\bm{Y}(x,y)\cdot d\bm{x}=\di\sum_i(\mathrm{tot}\,\bm{Y}(x_i,y_i))_z\vd x_i\vd y_i$
$\hspace{32mm}=\di\int_{S’}(\mathrm{rot}\,\bm{Y}(x,y))_zdS’\qquad\cdots\,$(18)

これが２次元のストークスの定理である。
この定理から$\,\mathrm{rot}\,\bm{X}_x(\bm{x})=0\,$のとき、以下の式がなりたつ。

$quad\di\int_C\bm{X}(\bm{x})\cdot d\bm{x}=0\qquad\cdots\,$(19)
閉曲線$\,C\,$の周りの１周の線積分を図のように
P点から出発してＱ点にいたる２つの曲線$\,C_1\,$と$\,C_2\,$上の線積分に分解すると

$\di\int_{\mathrm{P},C_1}^{\mathrm{Q}}\bm{X}(\bm{x})\cdot d\bm{x}+\di\int_{\mathrm{Q},C_2}^{\mathrm{P}}\bm{X}(\bm{x})\cdot d\bm{x}$
$\hspace{10mm}=\di\int_{\mathrm{P},C_1}^{\mathrm{Q}}\bm{X}(\bm{x})\cdot d\bm{x}-\di\int_{\mathrm{P},C_2}^{\mathrm{Q}}\bm{X}(\bm{x})\cdot d\bm{x}=0$

従って、点Pから点Qまでの線積分
$\quad\di\int_{\mathrm{P}}^{\mathrm{Q}}\bm{X}(\bm{x})\cdot d\bm{x}\qquad\cdots\,$(20)$\qquad$は途中の道筋によらず一定の値を取る。

すなわち、２点間の線積分が途中の道筋によらず一定の値を取るための必要かつ十分な条件は
$\quad\mathrm{rot}\,\bm{X}(\bm{x})=0\quad\cdots\,$(21)$\quad$が成立することである。

(2) 静電ポテンシャル

静電場が式(21)を満たすか、検証する。
まず、単位体積中の電荷量、つまり電荷密度を$\,\rho(\bm{x}_i)\,$とすると、電場$\,\bm{E}(\bm{x})\,$は

$\bm{E}(\bm{x})=\dfrac{1}{4\pi\ve}\di\int_{-\infty}^{\infty}d^3x’\dfrac{(\bm{x}-\bm{x}’)\rho(\bm{x}’)}{|\bm{x}-\bm{x}’|^3}\qquad\cdots\,$(22)

ここで、まず次の微分の計算をする。

$\pdr{}{x}\dfrac{1}{|\bm{x}-\bm{x}’|^n}=-n\dfrac{x-x’}{|\bm{x}-\bm{x}’|^{n+2}}\qquad\cdots\,$(23)

次に$\,\mathrm{rot}\,\bm{E}(\bm{x})\,$の$\,x\,$成分を計算する。式(22) から、

$\pdr{E_x(\bm{x})}{y}-\pdr{E_y(\bm{x})}{x}$
$\hspace{10mm}=\dfrac{1}{4\pi\ve_0}\di\int_{-\infty}^{\infty}d^3x’\rho(\bm{x}’)\left[(z-z’)\pdr{}{y}\dfrac{1}{|\bm{x}-\bm{x}’|^3}-(y-y’)\pdr{}{x}\dfrac{1}{|\bm{x}-\bm{x}’|^3}\right]$
$\hspace{10mm}=-\dfrac{3}{4\pi\ve_0}\di\int_{-\infty}^{\infty}d^3x’\rho(\bm{x}’)\left[\dfrac{(z-z’)(y-y’)}{|\bm{x}-\bm{x}’|^3}-\dfrac{(y-y’)(z-z’)}{|\bm{x}-\bm{x}’|^3}\right]=0\qquad\cdots\,$(24)

$y\,$成分、$z\,$成分についても同様である。よって静電場において$\quad\mathrm{rot}\,\bm{E}(\bm{x})=0\qquad\cdots\,$(25)$\quad$が成り立つ。

式(14)と式(25)を満たしている静電場$\quad\bm{E}(\bm{x})\,$は、ポテンシャル関数$\,\phi(\bm{x})\,$の勾配(gradient)で表す事が出来る。

$\bm{E}(\bm{x})=-\mathrm{grad}\,\phi(\bm{x})\qquad\cdots\,$(26)

この関数$\,\phi(\bm{x})\,$を 静電ポテンシャル という。
式(22)と(23)から、以下の式が得られる。

$\bm{E}(\bm{x})=-\dfrac{1}{4\pi\ve_0}\,\mathrm{grad}_x\di\int_{-\infty}^{\infty}d^3x’\dfrac{\rho(\bm{x}’)}{|\bm{x}-\bm{x}’|}\qquad\cdots\,$(27)

ここで、$\mathrm{grad}_x\,$は変数$\,x,y,z\,$による微分を取ることを意味する。
式(26)と式(27)から

$\phi(\bm{x})=\dfrac{1}{4\pi\ve_0}\di\int_{-\infty}^{\infty}d^3x’\dfrac{\rho(\bm{x}’)}{|\bm{x}-\bm{x}’|}\qquad\cdots\,$(28)

が成り立つ。
$\star\,$ガウスの法則より、電場の発散は式(14)から$\quad\nabla\cdot\bm{E}(\bm{x})=\rho(\bm{x})/\ve_0\qquad\cdots\,$(29)$\quad$となる。

4.電荷のテスト

２次元のベクトル場を設定する

適当な座標に正負の電荷をおく

numpy.gradient 関数を使ってベクトル場を計算する

ベクトル場の流線を表示する（正電荷から負電荷へと向かうよう符号を逆にする）

ベクトル場から発散を計算し電荷密度分布を表示する

参考資料

電磁気学　砂川重信　（岩倉書店）　物理テキストシリーズ

演習しよう　電磁気学　（数理工学社）　ライブラリ　物理の演習しよう２

In [85]:

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib   # 日本語表示用

#グラフ範囲を指定
LX, LY = 2.2, 2.2
# ベクトル場のベクトルの間隔の変数を gw とする
gw = 0.05
nn=int(2*LX/gw)   # 本数
coords,ds = np.linspace(-LX,LX,nn,retstep=True) # 座標と刻み幅の等差数列
# k = 4Πε0
k = 1.
x, y= np.meshgrid(coords, coords)    # x,y メッシュグリッド作成

# 点電荷の座標 (x1,y1), 電荷 q1
x_1,y_1,q_1 = -1.1, 0.2, 1
# (x1,y1) にある電荷から、点 (x,y) までの距離
r_1=np.sqrt((x-x_1)**2+(y-y_1)**2) 
# 点電荷の座標 (x2,y2), 電荷 q2
x_2,y_2,q_2 = 1, -0.9, -1   
# (x2,y2) にある電荷から、点 (x,y) までの距離
r_2=np.sqrt((x-x_2)**2+(y-y_2)**2) 

# 静電ポテンシャル phi は
phi=1/k*(q_1/r_1+q_2/r_2)
# 電場ベクトル Ex , Ey
E_y,E_x =np.gradient(phi, ds)

# x,yの描画範囲の設定
fig=plt.figure()
plt.xlim([-LX,LX])
plt.ylim([-LY,LY])
# グラフ描画
plt.grid()
plt.plot(x_1,y_1,'o',color='b')
plt.text(x_1+0.1,y_1+0.1,r'$q_1=+1$',color='b')
plt.plot(x_2,y_2,'o',color='r')
plt.text(x_2+0.1,y_2+0.1,r'$q_2=-1$',color='r')

# 電場ベクトルをプロット　 (+) から (-) に向くようにベクトルの向きを反対に
plt.streamplot(x,y,-E_x,-E_y,linewidth=0.3)
# タイトル
plt.text(x_1-0.2,1.5,"電場ベクトル表示",fontsize=25,color='m')
# ファイル保存
fig.savefig("electric_field.png")
plt.show()

# 電荷密度の計算
div_E=E_x-E_y

# 電荷密度の等高線をプロット
# x,yの描画範囲の設定
fig, ax = plt.subplots()
plt.xlim([-LX,LX])
plt.ylim([-LY,LY])
# グラフ描画
plt.grid()
#plt.plot(x_1,y_1,'o',color='b')
plt.text(x_1+0.1,y_1+0.1,r'$q_1=+1$',color='b')
#plt.plot(x_2,y_2,'o',color='r')
plt.text(x_2+0.1,y_2+0.1,r'$q_2=-1$',color='r')

# 電荷分布
CS = ax.contourf(x, y, div_E)
#fig.colorbar(CS)
# タイトル
plt.text(x_1,1.5,"電荷密度分布",fontsize=25,color='m')
# ファイル保存
fig.savefig("charge_distribution-2.png")
plt.show()

No description has been provided for this image

In [ ]:

傾きの計算

Gradient-1

$\def\bm{\boldsymbol}$$\def\di{\displaystyle}$$\def\ve{\varepsilon_0}$$\newcommand{\pdr}[2]{\dfrac{\partial #1}{\partial #2}}$$\newcommand{\ppdr}[2]{\dfrac{\partial^2 #1}{\partial #2}}$

グラジエントのテスト

2次元でのテスト

grad(z) $\equiv\left(\dfrac{\partial z}{\partial x},\dfrac{\partial z}{\partial y}\right)$

python の numpy の gradient関数は、中心差分であり、始点側は後退差分、終点側は前進差分としている。
source と destnation の要素数が同じである。

diff関数は前進差分で、要素数が１つ減る。

前進差分

$\dfrac{du}{dx}=\displaystyle\lim_{h\to\ 0}\dfrac{u(x+h)-u(x)}{h}$

中心進差分

$\dfrac{du}{dx}=\displaystyle\lim_{h\to\ 0}\dfrac{u(x+h)-u(x-h)}{2h}$

後退差分

$\dfrac{du}{dx}=\displaystyle\lim_{h\to\ 0}\dfrac{u(x)-u(x-h)}{h}$

テスト

平面座標から山の高さを返す関数を作り、 x, y, z 軸での標高線を描く

表面をワイヤーフレームで表示する

x , y のメッシュグリッドを作成し、そのメッシュグリッドで山の高さを計算する

ｚ軸からの等高線グラフに、微分データ(Gradient)のベクトルを表示する

山データから高さを y 軸に平行な線で区切ったデータでプロットする

微分データから高さを y 軸に平行な線で区切ったデータでプロットする

In?[82]:

import numpy as np
import pylab as plt
from mpl_toolkits.mplot3d import Axes3D

def yama(x1, y1):
    h = 15 - np.sqrt((x1+10)**4 +(y1+6)**2)*0.015-np.sqrt((x1-20)**2+(y1-15)**2)*0.12
    return h
MAX_R=25
MIN_R=-25
MESH=2.5
fig = plt.figure()
ax = fig.add_subplot(projection='3d')

x = np.arange(MIN_R, MAX_R, MESH)    # 1次元のリスト
y = np.arange(MIN_R, MAX_R, MESH)

print('◆　データ数    x : ',len(x),'   y : ',len(y))

X, Y = np.meshgrid(x, y)             # 2次元のリスト
Z = yama(X,Y)                        # 2次元のリストからの変数なので Z は２次元
Z[np.less(Z, 0)] = 0
dZ_dX, dZ_dY = np.gradient(Z)  # Z が２次元あので、微分すると２次元変数が２つとなる

ax.contour(X, Y, Z, zdir='z', offset=0, cmap=plt.cm.Reds)
ax.contour(X, Y, Z, zdir='x', offset=MIN_R, cmap=plt.cm.OrRd)
ax.contour(X, Y, Z, zdir='y', offset=MAX_R, cmap=plt.cm.Greens)
ax.set_zlim(0, 16)
ax.plot_wireframe(X, Y, Z ,linewidth=0.3)
plt.show()

print('\n 傾斜のベクトルは下から上ではなく、上から下になるように向きを逆にしている\n')

fig, ax = plt.subplots(figsize=(5,5))
ax.contour(X, Y, Z,cmap=plt.cm.Reds)
ax.quiver(X, Y, -dZ_dY, -dZ_dX, angles="xy", scale_units='xy', scale=0.7,color='b')
plt.show()

print('\n 地形をグラフとして表わす\n')

fig, ax = plt.subplots(figsize=(5,5))
plt.plot(X[0],Z[0],linewidth=0.3,color='r',label='x=-20')
plt.plot(X[2],Z[2],linewidth=0.3,color='g',label='x=-16')
plt.plot(X[4],Z[4],linewidth=0.3,color='b',label='x=-12')
plt.plot(X[6],Z[6],linewidth=0.3,color='y',label='x=-8')
plt.plot(X[8],Z[8],linewidth=0.3,color='m',label='x=-4')
plt.plot(X[10],Z[10],linewidth=0.3,color='c',label='x=0')
plt.plot(X[15],Z[15],linewidth=0.3,color='k',label='x=10')
plt.legend()
plt.show()

print('\n 傾きをグラフとして表わす\n')

fig, ax = plt.subplots(figsize=(5,5))
plt.ylim(-0.6,0.6)
plt.plot(X[0],dZ_dX[0],linewidth=0.4,color='r',label='x=-20')
plt.plot(X[8],dZ_dX[8],linewidth=0.4,color='g',label='x=-4')
plt.plot(X[12],dZ_dX[12],linewidth=0.4,color='b',label='x=4')
plt.plot(X[15],dZ_dX[15],linewidth=0.4,color='c',label='x=10')
plt.plot(X[19],dZ_dX[19],linewidth=0.4,color='m',label='x=18')
plt.legend()
plt.show()

◆　データ数    x :  20    y :  20

 傾斜のベクトルは下から上ではなく、上から下になるように向きを逆にしている

 地形をグラフとして表わす

 傾きをグラフとして表わす

In?[?]:

ラグランジュ微分

$\def\bm{\boldsymbol}$$\def\di{\displaystyle}$$\def\ve{\varepsilon_0}$$\def\dd#1#2{\dfrac{\partial #1}{\partial #2}}$$\def\dda#1#2{\dfrac{\partial^2 #1}{\partial #2}}$

1. 流体粒子と流体運動の扱い

流体を考える際、2つの捉え方がある。
[1]　ラグランジュの方法（ Lagrange ）
物体（固体）の運動と同様、各流体粒子に着目して、各流体粒子が時間の経過とともに、どのように動くかを追跡していく方法である。
この方法は、一つの流体粒子の経路や加速度を知る上では便利ではあるが、流れ場が全体的にどのようになっているかを知るには適さない。
[2]　オイラーの方法（ Euler ）
この方法は、特定の流体粒子を追跡するのではなく、流れ場全体の様子をそれぞれの時刻に一度に調べる方法である。すなわち、流速や圧力を、座標$\,\,x\,,\,y\,,\,z\,,\,$および時間$\,t\,$の関数として表す。この方法は、流体の運動を調べる流体力学において、一般に用いられる方法である。

2. テーラー展開

まずは、数学の準備をします。
[1]　1 変数でのテーラー展開
$\quad$関数$\,f(x)\,$において、点$\,a\,$の周りでテーラー展開すると
\begin{equation}f(x)=f(a)+f^{\prime}(a)(x-a)+\dots+\dfrac{f^{(n)}(a)}{n!}(x-a)^n+\cdots
\end{equation}$\quad$ここで、$\,x\,\to\,x+\Delta x\,\quad a\,\to\,x\,$ と置き換えると
\begin{equation}
f(x+\Delta x)=f(x)+(\Delta x)\,f^{\prime}(x)+\dfrac{(\Delta x)^2}{2!}f^{\prime\prime}(x)+\cdots+\dfrac{(\Delta x)^n}{n!}f^{(n)}(x)+\cdots
\end{equation}[2]　多変数のテーラー展開\begin{align}f(x+\Delta x,& y+\Delta y,z+\Delta z)=f(x,y,z)+\left(\Delta x \dd{}{x}+\Delta y\dd{}{y}+\Delta z\dd{}{z}\right)f(x,y,z)\\ &+\dfrac{1}{2!}\left(\Delta x \dd{}{x}+\Delta y\dd{}{y}+\Delta z\dd{}{z}\right)^2f(x,y,z)+\cdots \end{align}$\quad$ここで、$\bm{x}=^t(\,x,\,y,\,z)\,\,\,\,\bm{h}=^t(\Delta x,\Delta y,\Delta z)\,$とおくと、\begin{equation} f(\bm{x}+\bm{h})=f(\bm{x})+\sum_{n=0}^{\infty}\dfrac{1}{n!}(\nabla\cdot\bm{h})^nf(\bm{x})\qquad\text{と表すことができる}\end{equation}

3. ラグランジュ微分

ラグランジュ微分とは、オイラーの方法とラグランジュの方法の両方の流儀を混ぜ合わせたような概念である。時々刻々と移動していく流体の「ある一部分」を追いかけながら、その「一部分」が持つ物理量$\,A\,$の時間的な変化を考える。
時刻$\,t\,$に、位置$\,\bm{x}=(x,y,z)\,$にある速度$\,\bm{u}=(u_x,u_y,u_z)\,$の流体の持つ物理量を$\,A(x,y,z,t)\,$と表す。$\,\Delta t\,$秒後にはこの流体はおよそ$\,(\,x+u_x\Delta t,\,y+u_y\Delta t,\,z+u_z\Delta t\,)\,$付近に移動していることであろう。つまり、$\,\Delta t\,$秒後がの移動後の地点での物理量は$\,A(x+u_x\Delta t,y+u_y\Delta t,z+u_z\Delta t,t+\Delta t)\,$となる。
これをテーラー展開の一次で近似すると\begin{align}A(x+u_x\Delta t,& y+u_y\Delta t,z+u_z\Delta t,t+\Delta t)\\&\doteq A(x,y,z,t)+\dd{A}{x}u_x\Delta t+\dd{A}{y}u_y\Delta t+\dd{A}{z}\Delta t+\dd{A}{t}\Delta t\end{align}変化分を計算すると\begin{align}\Delta A&\doteq A(x+u_x\Delta t,y+u_y\Delta t,z+u_z\Delta t,t+\Delta t)-A(x,y,z,t)\\&\doteq\dd{A}{x}u_x\Delta t+\dd{A}{y}u_y\Delta t+\dd{A}{z}u_z\Delta t+\dd{A}{t}\Delta t\\&=\left(\dd{A}{x}u_x+\dd{A}{y}u_y+\dd{A}{z}u_z+\dd{A}{t}\right)\Delta t\qquad\cdots\quad\text{(1)}\end{align}これを時間経過による変化割合で表すと\begin{equation}\dfrac{\Delta A}{\Delta t}\doteq\dd{A}{x}u_x+\dd{A}{y}u_y+\dd{A}{z}u_z+\dd{A}{t}\qquad\cdots\quad\text{(2)}\end{equation}(1)式の近似には$\,\Delta t\,$の2乗以上に比例する程度の誤差があり、それを$\,\Delta t\,$で割った(2)式には$\,\Delta t\,$あるいは$\,\Delta t\,$の2乗以上に比例するような誤差が含まれているが、ここで$\,\Delta t\,\to\,0\,$の極限を考えれば無視できるようになるので、それを等式を使って次のように表す。\begin{equation}\dfrac{DA}{Dt}=\dd{A}{x}u_x+\dd{A}{y}u_y+\dd{A}{z}u_z+\dd{A}{t}\qquad\cdots\quad\text{(3)}\end{equation}これが、「ラグランジュ微分」「物質微分」などと呼ばれているものである。これは、流体と一緒に流れている人から見た、その地点での物理量$\,A\,$の時間的な変化率である。
物理量$\,A\,$を省いて、順序を変えると以下のようになる。
\begin{equation}\dfrac{D}{Dt}\equiv u_x\dd{}{x}+u_y\dd{}{y}+u_z\dd{}{z}+\dd{}{t}=\bm{u}\cdot\nabla+\dd{}{t}\quad\cdots\quad\text{(4)}\end{equation}流体の加速度をその点での微分とラグランジュ微分で比べたのが、下の図である。

光の速度

$\def\bm{\boldsymbol}$
$\def\di{\displaystyle}$
$\def\ve{\varepsilon_0}$
$\def\dd#1#2{\dfrac{\partial #1}{\partial #2}}$
$\def\dda#1#2{\dfrac{\partial^2 #1}{\partial #2}}$
オーソドックスな形で、光（電磁波）の真空中の速度を求めてみる。

［１］マックスウェル方程式

光も電磁波なので、マックスウェルの方程式に従う。マックスウェル方程式は４つに分けられる。
(1)電場の発散
\[\mbox{div }\bm{E}=\nabla\cdot\bm{E}=\dfrac{\rho}{\ve}\tag{1.1}\]
電場の源が電荷であり、電場が電荷から放射状であることを表す。
ここで $\,\rho\,$は電荷密度で、$\ve\,$は真空の誘電率である。
(2)電場の回転
\[\mbox{rot }\bm{E}=\nabla\times\bm{E}=-\dd{\bm{B}}{t}\tag{1.2}\]
磁束密度の変化により電場が生じる　Faradayの法則=電磁誘導の法則
(3)磁場の発散
\[\mbox{div }\bm{B}=\nabla\cdot\bm{B}=0\quad\tag{1.3}\]
磁場には源がない
(4)磁場の回転
\[\mbox{rot }\bm{B}=\nabla\times\bm{B}=\mu_0(\bm{j}+\ve\dd{\bm{E}}{t})\tag{1.4}\]
電流及び電場の変化が磁場を生むことを表す。Ampére-Maxwellの法則
ここで$\,\mu_0\,$は真空の透磁率である。

［２］マックスウェル方程式の展開

真空中を伝わる電磁波について考えたいので, 電荷密度はいたるところで$\,0\,$であるとする. よって電流密度も$\,0\,$であるので、次の４つの式が得られる。
\begin{align}
\mbox{div }\bm{E}&=0 \tag{2.1}\\
\mbox{rot }\bm{E}&=-\dd{\bm{B}}{t} \tag{2.2}\\
\mbox{div }\bm{B}&=0 \tag{2.3}\\
\mbox{rot }\bm{B}&=\mu_0\ve\dd{\bm{E}}{t} \tag{2.4}
\end{align}
場の回転を改めて場とみなして、回転を調べる。式$\,(2.2)\,$を回転すると
\begin{align}
\nabla\times(\nabla\times\bm{E})&=-\dd{}{t}(\nabla\times\bm{B})\\
&=-\mu_0\dd{}{t}\left(\bm{j}+\ve\dd{\bm{E}}{t}\right)\\
&=-\mu_0\dd{\bm{j}}{t}-\mu_0\ve\dda{\bm{E}}{t^2}\tag{2.5}
\end{align}
となり、電流密度の他には電場のみの閉じた形となる。ここでは、ベクトル解析のベクトルの回転の回転からラプラシアンを導く、以下の公式を用いる。
\[\nabla\times(\nabla\times\bm{A})=\nabla(\nabla\cdot\bm{A})-\Delta\bm{A}\qquad\because\,\,\Delta\equiv\nabla\cdot\nabla\tag{2.6}\]
この公式を$\,(2.5)\,$式の右辺に適用する。
\begin{align}
\nabla\times(\nabla\times\bm{E})&=\nabla(\nabla\cdot\bm{E})-\Delta\bm{E}\\[3pt]
&=0-\Delta\bm{E}\qquad\,\because\,\,\nabla\cdot\bm{E}=0\quad(2.1)\,\,\text{より}\\[3pt]
&=-\Delta\bm{E}\tag{2.7}
\end{align}
$\,(2.5)\,$式と$\,(2.6)\,$をあわせると
\[\Delta\bm{E}-\mu_0\ve\dda{\bm{E}}{t^2}-\mu_0\dd{\bm{j}}{t}=0\tag{2.8}\]
ここの電流は$\,0\,$なので、第3項は消せる。ここで、$x\,$成分で考えると。
\[\dda{\bm{E}}{x^2}-\mu_0\ve\dda{\bm{E}}{t^2}=0\tag{2.10}\]
の形の波動方程式が得られる。

［3］波動方程式の一般解

この方程式の解は次のような形で表される。例えば$\,\bm{E}\,$の振幅を$\,z\,$軸にとると、解は
\[E_z=f(x-vt)+g(x+vt)\tag{3.1}\]
の形で表せる。ここで、$f\,$と$\,g\,$は任意の関数であり、$f(x − vt)\,\,$は$\,x\,$軸の正の向きに速さ$\,v\,$で
進む波動を表し、$g(x + vt)\,\,$は$\,x\,$軸の負の向きに速さ$\,v\,$で進む波動を表す。
ここで、式$\,(2.2)\,$を成分に分解する。
\begin{align}
\dd{E_z}{y}-\dd{E_y}{z}&=-\dd{B_x}{t}\\
\dd{E_x}{z}-\dd{E_z}{x}&=-\dd{B_y}{t}\\
\dd{E_y}{x}-\dd{E_x}{y}&=-\dd{B_z}{t}
\end{align}
ここで、$E_x=0\,\,,\,\,E_y=0\,$なので、次のような結果となる
\begin{align}
\dd{B_x}{t}&=0\\
\dd{B_y}{t}&=f^{\prime}(x-vt)+g^{\prime}(x+vt) \tag{3.2}\\
\dd{B_z}{t}&=0
\end{align}
式$\,(3.2)\,$を$\,t\,$で積分すると
\[B_y=-\dfrac{1}{v}f(x-vt)+\dfrac{1}{v}g(x+vt)\tag{3.3}\]
となる。つまり、$E_z\,$と$\,B_y\,$は、同じ関数$\,f\,$と$\,g\,$で表され、両者が互いに組み合って、離れることなく、同じ速さ$\,v\,$を持つ波動となって$\,x\,$軸を伝搬する。

電場と磁場の進行波

［4］電磁波の伝搬する速さ

波動方程式の一般解と波動方程式を再掲する。
\begin{align}
&E_z=f(x-vt)+g(x+vt)\tag{3.1}\\
&\dda{\bm{E}}{x^2}-\mu_0\ve\dda{\bm{E}}{t^2}=0\tag{2.10}
\end{align}
この$\,(3.1)\,$式を$\,(2.10)\,$に代入する。このとき、$x-vt=p\,\,,\,\,x+vt=q\,\,$とする。
\[\dd{E_z}{x}=\dd{f}{x}+\dd{g}{x}=\dd{f}{p}\dd{p}{x}+\dd{g}{q}\dd{q}{x}=\dd{f}{p}+\dd{g}{q}\quad\text{なので}\]
\[\dda{E_z}{x^2}=\dda{f}{p^2}+\dda{g}{q^2}\qquad\text{となる。次に時間で微分する。}\]
\[\dd{E_z}{t}=\dd{f}{t}+\dd{g}{t}=\dd{f}{p}\dd{p}{t}+\dd{g}{q}\dd{q}{t}=-v\dd{f}{p}+v\dd{g}{q}\quad\text{なので}\]
\[\dda{E_z}{t^2}=v^2\dda{f}{p^2}+v^2\dda{g}{q^2}=v^2\dda{E_z}{x^2}\qquad\text{となるので}\quad (2.10)\,\text{より}\]
\[v^2=\dfrac{1}{\mu_0\ve}\qquad\text{よって}\qquad v=\dfrac{1}{\sqrt{\mu_0\ve}}\tag{4.1}\]
真空の誘電率$\,\ve\,$と透磁率$\,\mu_0\,$の値

$\qquad\ve=\dfrac{10^7}{4\pi c^2}\quad[\,\mathrm{C}\cdot\mathrm{N}^{-1}\cdot\mathrm{m}^{-2}\,\,]\hspace{20mm}\mu_0=4\pi\times 10^{-7}\quad[\,\,\mathrm{N}\cdot\mathrm{A}^{-2}\,\,]\quad$を代入すると

$\qquad\quad v=\dfrac{1}{\sqrt{\mu_0\ve}}=c\qquad$となり、電磁波の速度が光速と一致する。

まあ、誘電率の定義からして、光速を使っているので当然の結果である。

二重振り子

1.経緯

放送大学の「物理と化学のための数学演習」という授業のレポートの課題のひとつに「二重振り子」があったので、忘れないようにここにメモっておきます。

2.レポート課題

天井から長さ $\ell$ の紐で吊るされた質量 $M$ の錘に、もう一つの同じ長さ $\ell$ の紐で同じ質量の錘が垂れ下がった、二重振り子の微小振動を考える。この問題は自由度２の連成振動となっている。以下の問いに答えよ。
$\textbf{[1]}$ それぞれの紐が鉛直線となす角度を $\theta_1\,,\,\theta_2\,$とし、近似式、$\sin\theta\simeq\theta\,$を用いて、２つの錘の運動方程式を導き、この連成振動の基準座標と基準振動数を求めよ。紐の質量は小さいとして無視する。
$\textbf{[2]}$ ２つの紐を変形しない同じ質量 $m$ の棒で置き換えるとどうなるか。棒の重心はその真ん中にあるとする。

※　2. の問題は、私のやり方が拙かったせいか、解析解が得られませんでした。そこで、1. だけをここにメモります。

3.方程式の導出

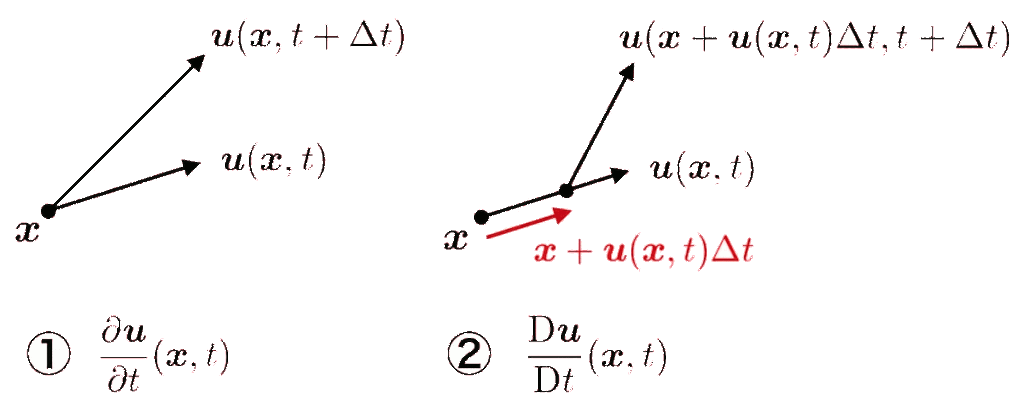
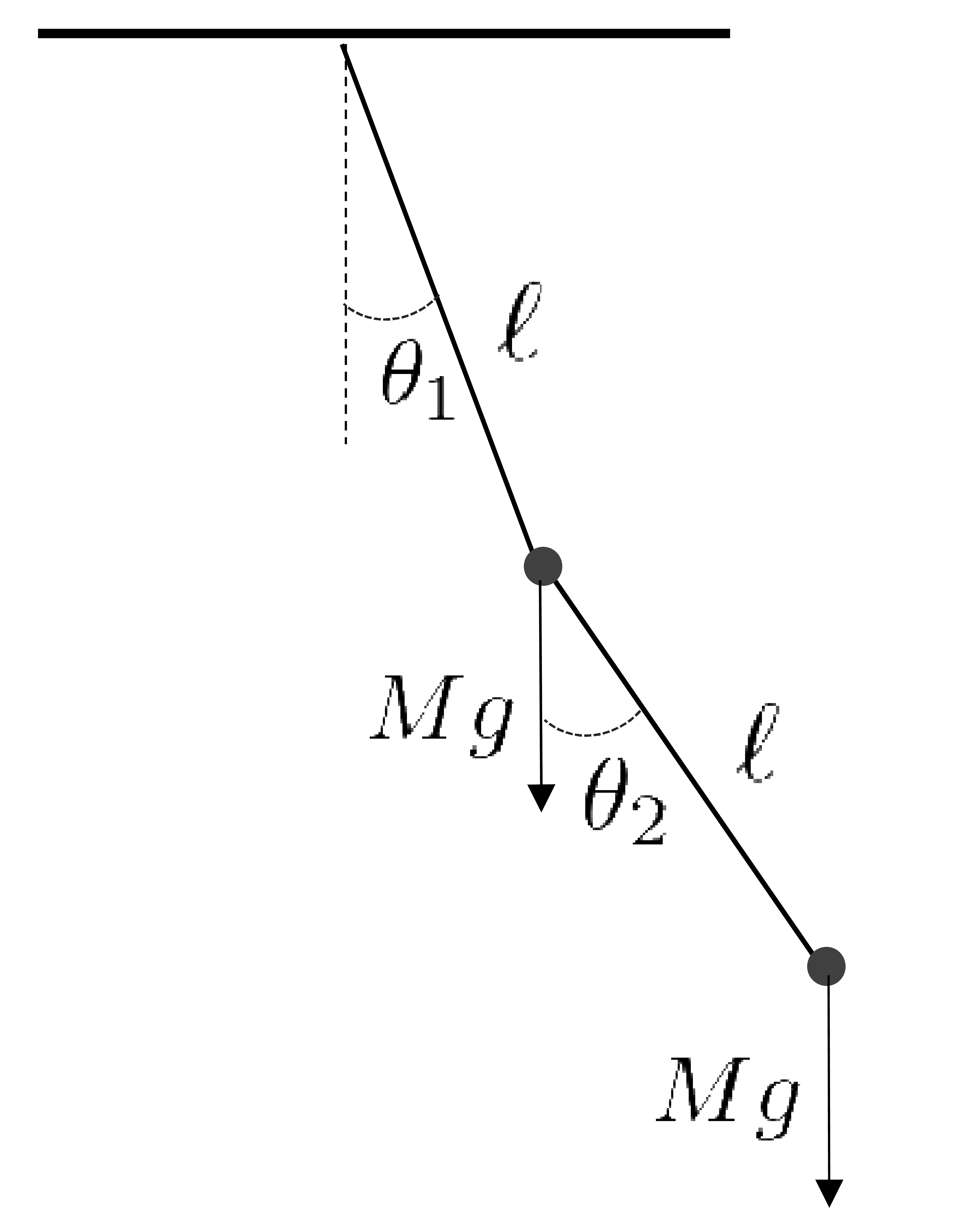最初のオモリの座標を $(x_1,y_1)\,$ , そこから垂れ下がったオモリの座標を $(x_2,y_2)\,$ とする。

$x_1=\ell\sin\theta_1\qquad y_1=-\ell\cos\theta_1$
$x_2=x_1+\ell\sin\theta_2=\ell(\sin\theta_1+\sin\theta_2)$
$y_2=y_1-\ell\cos\theta_2=-\ell(\cos\theta_1+\cos\theta_2)$
$\dot{x}_1=\ell\cos\theta_1\dot{\theta}_1\simeq\ell\dot{\theta}_1$
$|\dot{x}_1|^2=\ell^2\dot{\theta}_1^2$
$\dfrac{1}{2}|\dot{x}_1|^2=\dfrac{\ell^2}{2}\dot{\theta}_1^2$
$\dot{x}_2=\ell(\cos\theta_1\dot{\theta}_1+\cos\theta_2\dot{\theta}_2)\simeq\ell(\dot{\theta}_1+\dot{\theta}_2)$
$\dfrac{1}{2}|\dot{x}_2|^2=\dfrac{\ell^2}{2}(\dot{\theta}_1+\dot{\theta}_2)^2$

$\theta_1\,,\,\theta_2\,$が小さいとするので、運動エネルギーは $\quad T=\dfrac{M\ell^2}{2}\dot{\theta}_1^2+\dfrac{M\ell^2}{2}(\dot{\theta}_1+\dot{\theta}_2)^2$

ポテンシャル・エネルギーは$\quad U=-Mg\ell(\cos\theta_1+\cos\theta_1+\cos\theta_2)$

よって、ラグラジアン$\,L\,$は

$L=T-U=\dfrac{M\ell^2}{2}(2\dot{\theta}_1^2+2\dot{\theta}_1\dot{\theta}_2+\dot{\theta}^2)+Mg\ell(2\cos\theta_1+\cos\theta_2)$

$\dfrac{\partial L}{\partial\theta_1}\,=-2Mg\ell\sin\theta_1\simeq -2Mg\ell\theta_1\hspace{12mm}\dfrac{\partial L}{\partial\dot{\theta}_1}=M\ell^2(2\dot{\theta}_1+\dot{\theta}_2)$

$\dfrac{\partial L}{\partial\theta_2}\,=-Mg\ell\sin\theta_2\simeq -Mg\ell\theta_2\hspace{16mm}\dfrac{\partial L}{\partial\dot{\theta}_2}=M\ell^2(\dot{\theta}_1+\dot{\theta}_2)$

オイラー・ラグランジュ方程式は$\quad\dfrac{d}{dt}\left(\dfrac{\partial L}{\partial\dot{q}_1}\right)=\dfrac{\partial L}{\partial q}\,\,$なので

$2\ddot{\theta}_1+\ddot{\theta}=-2\dfrac{g}{\ell}\theta_1\qquad \ddot{\theta}_1+\ddot{\theta}_2=-\dfrac{g}{\ell}\theta_2\quad$の関係が得られる。
これより
$\left(\begin{array}{@{\,}c@{\,}}\ddot{\theta}_1\\[2pt] \ddot{\theta}_2\end{array}\right)=\dfrac{g}{\ell}\left(\begin{array}{@{\,}rr@{\,}}-2&1\\[2pt]2&-2\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt] \theta_2\end{array}\right)\qquad$の連立微分方程式が導かれる。
$\hspace{28mm}$行列$\,\,K\,$

4.方程式の解法

この行列 $K$ を対角化することで、方程式を解く。まず $K$ の固有値と固有ベクトルを求める。
固有値 $\lambda$ は、固有ベクトル $\textbf{x}$ と $K\textbf{x}=\lambda\textbf{x}$ の関係にあるので、$\det{(K-\lambda I)}=0$ より
$\lambda^2+4\lambda+2=0\qquad \lambda=-2\pm\sqrt{2}\qquad$が得られる。

$\textbf{(4-1)} \,\,\lambda_1=-2+\sqrt{2}$ のとき

$\quad(K-\lambda_1 I)=\left(\begin{array}{@{\,}rr@{\,}}-\sqrt{2}&1\\[2pt]2&-\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}x_1\\[2pt] x_2\end{array}\right)=0\qquad$ より

$\quad x_1=\dfrac{1}{\sqrt{3}}\qquad x_2=\dfrac{\sqrt{2}}{\sqrt{3}}\qquad\quad \textbf{x}_1=\left(\begin{array}{@{\,}r@{\,}}\frac{1}{\sqrt{3}}\\[2pt]\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)$

$\textbf{(4-2)} \,\,\lambda_2=-2-\sqrt{2}$ のとき

$\quad(K-\lambda_2 I)=\left(\begin{array}{@{\,}rr@{\,}}\sqrt{2}&1\\[2pt]2&\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}x_1\\[2pt] x_2\end{array}\right)=0\qquad$ より

$\quad x_1=\dfrac{1}{\sqrt{3}}\qquad x_2=-\dfrac{\sqrt{2}}{\sqrt{3}}\qquad\quad \textbf{x}_2=\left(\begin{array}{@{\,}r@{\,}}\frac{1}{\sqrt{3}}\\[2pt]-\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)$

5.正則行列の逆行列

固有ベクトルを縦に並べた行列 $P$ を用いて $P^{-1}KP$ として $K$ を対角化する。

$\quad P=\left(\begin{array}{@{\,}rr@{\,}}\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{3}}\\[3pt]\frac{\sqrt{2}}{\sqrt{3}}&-\frac{\sqrt{2}}{\sqrt{3}}\end{array}\right)\qquad\quad P^{-1}=\left(\begin{array}{@{\,}rr@{\,}}\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{2\sqrt{2}}\\[3pt]\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2\sqrt{2}}\end{array}\right)$

この $P^{-1}$ を用いて、新しい変数 $\Theta_1\,\,,\,\,\Theta_2\,\,$を定義する。

$\quad\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)=P^{-1}\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt]\theta_2\end{array}\right)=\left(\begin{array}{@{\,}rr@{\,}}\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{2\sqrt{2}}\\[3pt]\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2\sqrt{2}}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\theta_1\\[2pt]\theta_2\end{array}\right)$

元の連立微分方程式は、変数　$\Theta_1\,\,,\,\,\Theta_2$\,\,$に対する以下の微分方程式と等価である。

$\quad\dfrac{d}{dt}\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)=\dfrac{g}{\ell}\left(\begin{array}{@{\,}rr@{\,}}-2+\sqrt{2}&0\\[3pt]0&-2-\sqrt{2}\end{array}\right)\left(\begin{array}{@{\,}c@{\,}}\Theta_1\\[2pt] \Theta_2\end{array}\right)$

最終的に、運動は２つの固有振動の足し合わせで表され、それぞれの固有振動数 $\omega_1\,\,,\,\,\omega_2\,\,$は、

$\quad\omega_1=\sqrt{2+\sqrt{2}}\sqrt{\dfrac{g}{\ell}}\quad,\quad \omega_1=\sqrt{2-\sqrt{2}}\sqrt{\dfrac{g}{\ell}}\quad$ となる。

弾性衝突

放送大学のオンライン授業で「力学演習」を履修している。そこでの練習問題で一次元の弾性衝突問題があり、すっかり忘れているので再確認のため、計算してみました。

図のような２球で考える。向きは$\,x\,$軸方向に正として、初速度をそれぞれ$\,v_1\,\,,\,v_2\,$とする。衝突後の速度をそれぞれ$\,v_3\,\,,\,v_4\,$とする。弾性衝突なので、運動量とエネルギーが保存する。

・運動量保存
$\qquad m_A\,v_1+m_B\,v_2=m_A\,v_3+m_B\,v_4\quad\cdots\,$(1)
・エネルギー保存
$\qquad \dfrac{1}{2}m_A\,v_1^2+\dfrac{1}{2}m_B\,v_2^2=\dfrac{1}{2}m_A\,v_3^2+\dfrac{1}{2}m_B\,v_4^2\quad\cdots\,$(2)

式(1)から、$\quad v_4=\dfrac{m_A(v_1-v_3)+m_Bv_2}{m_B}\quad\cdots\,$(3)
式(2)から、$\quad v_4^2=\dfrac{m_A(v_1^2-v_3^2)+m_Bv_2^2}{m_B}\quad\cdots\,$(4)
式(3)を２乗すると、
$\quad v_4^2=\dfrac{m_A^2v_1^2-2m_A^2v_1v_3+m_A^2v_3^2+m_B^2v_2^2+2m_Am_Bv_1v_2-2m_Am_Bv_2v_3}{m_B^2}\quad\cdots\,$(5)
式 (4)$\,=\,$(5) なので、
$\quad m_Am_Bv_1^2-m_Am_Bv_3^2+m_B^2v_2^2$
$\qquad\qquad =m_A^2v_1^2-2m_A^2v_1v_3+m_A^2v_3^2+m_B^2v_2^2+2m_Am_Bv_1v_2-2m_Am_Bv_2v_3\quad\cdots\,$(6)

$\quad m_A^2v_1^2-2m_Av_1v_3+m_A^2v_3^2+2m_Am_Bv_1v_2-2m_Am_Bv_2v_3-m_Am_Bv_1^2+m_Am_Bv_3^2=0\,\cdots\,$(7)

$\quad(m_A+m_B)v_3^2-2(m_Av_1+m_Bv_2)v_3+m_Av_1^2+2m_Bv_1v_2-m_Bv_1^2=0\quad\cdots\,$(8)

この式(8) を$\,v_3\,$の２次方程式として解くと
$\quad v_3=\dfrac{m_Av_1+m_Bv_2\pm\sqrt{m_B^2(v_1-v_2)^2}}{m_A+m_B}=\dfrac{m_Av1+m_Bv_2\pm m_B|v_1-v_2|}{m_A+m_B}\quad\cdots\,$(9)

ここで、球 A の速度が B の速度より大きいケースで考えてみる。 $\,v_1\ge v_2$
$\,\pm\,$の$\,+\,$では、$\,v_3=v_1\,$となり、すり抜ける形なので$\,-\,$を採用する。

$\quad v_3=\dfrac{m_Av_1-m_Bv_1+2m_Bv_2}{m_A+m_B}\quad\cdots\,$(10)

ここで、両方の球の質量が同じ場合、$\,v_3=v_2\,$となり、A と B の運動量が入れ替わることになる。

◇ 大小球の正面衝突

大小の球を正面衝突させた場合を考える。
Ａは$\,m_A=3m\,$とし、Ｂは$\,m_B=m\,$とする。
速度はともに$\,v_1=v_2=v_0\,$(符号は正負となる)として、正面からの衝突とする。

式(10)と式(1)により

$\quad v_3=\dfrac{3mv_0-mv_0-2mv_0}{3m+m}=0\quad v_4=\dfrac{3mv_0-mv_0}{m}=2v_0\,$となる。

結局、Ａは停止しＢは速度$\,2v_0\,$で反対側に跳ね返ることになる。

◇ ３球での衝突問題

『中川のビジュアル物理学教室』のページの中の「解説：一次元衝突」に次のような３球の衝突が紹介されていました。(画像は中川氏のページのものを使わせてもらいました)

静止している球Ｂ，Ｃに，その２倍の質量をもつ球Ａを$\,v_0\,$で弾性衝突したらどうなるだろうか？

この問題は，過去に青学大の入試問題として出題されたことがあるという事でした。

まず、Ａが静止しているＢに衝突する時点を考える。式(10) に$\,m_A=2m\,,\,m_B=m\,,\,v_1=v_0\,,\,v_2=0\,$を代入すると、
$\quad v_A=v_3=\dfrac{2mv_0-mv_0}{3m}=\dfrac{1}{3}v_0\quad\cdots\,$(11)
静止していたＢの速さ$\,v_B\,$は、式(11)の値を式(1)に代入すると$\,v_B=v_4=\dfrac{4}{3}v_0\,$となる。
Ｂがこの速度$\,v_B\,$で、静止しているＣに衝突すると
ＢとＣは同質量なので、式(11)より、Ｂは停止してＣは速度$\,v_C=v_B\,$で動き出すことになる。
停止した(１回動いて停止した形になる)ＢにＡが$\,v_A=\dfrac{1}{3}v_0\,$で衝突することになる。
同じく、式(11)に代入すると、再度のＡの速度$\,v_A’\,$は
$\quad v_A’=\dfrac{2m\frac{1}{3}v_0-m\frac{1}{3}v_0}{3m}=\dfrac{1}{9}v_0\quad\cdots\,$(12)
これを式(1)に代入すると$\quad2m\dfrac{1}{3}=2m\dfrac{1}{9}v_0+mv_B’\,$より
Ａは$\,\dfrac{1}{9}v_0\,$で動き出し、Ｂは$\,\dfrac{4}{9}v_0\,$で動き出す。
Ｃは先程、Ｂの衝突で$\dfrac{4}{3}v_0\,$で動き出しているので、３球はバラバラになることになる。

振り子の実験

1.経緯

私が通学（通信制なので、通ってはいないが）している放送大学のゼミで、自宅での実験を動画撮影して皆で共有するという企画があったので、振り子の実験をやってみました。
振り子は小学$5$年生用の実験セットをAmazonから仕入れました。
（「ふりこのはたらき」 $730$円）

2.実験

ひもの長さは$30$cmとして、振れ角測定用に角度を書いた紙を付けました。大きく振った位置から重りを降ろした。
($2020.09.05$ 実施)
撮影は iPhone をそのままの設定で($30$f)三脚無しで行いました。時間は約$2$分間でした。
動画は DropBox 経由で、Windows マシンに落とした。再生で簡単にコマ落としが出来、時間の表示が $1/100$ 秒単位で出てくるので MovieMaker を使用した。（最近は MovieMaker はサポートされていないようですね）

撮影した動画の抜粋

編集は mac の iMovie を使用した。縦のプロジェクトが作れないので、ビデオクリップで横にして、編集して、出来た動画を QuickTime のplayer で開いて、縦に変換した。.mov 型の動画になるので、vlc で .mp4 に変換した。
（このページでは動画のサイズが$8$Mb なので抜粋版をつくりました）

3.実験結果

動画をMovieMaker でコマ落とし再生して、最大振幅の角度と時間を記録したのが下図です。

動画が$30$fなので、時間刻みが$1/30$sec単位となり、グラフは階段状になるが、振れ角が大きいと周期が長いという結果となった。

4.検討1：振幅の小さい場合

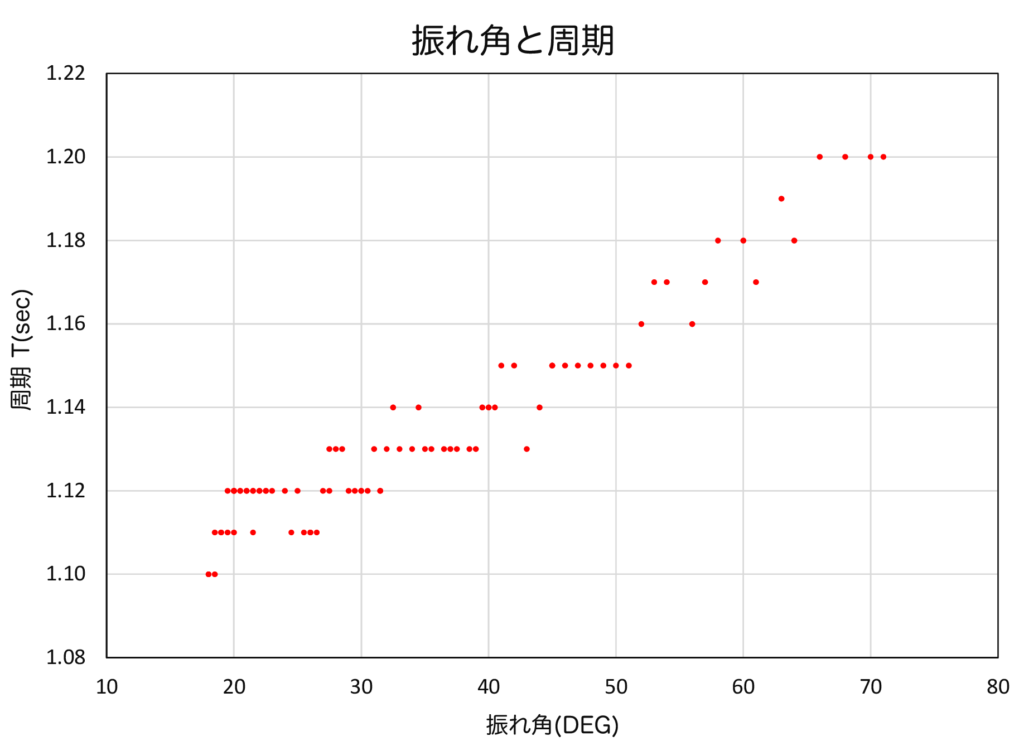
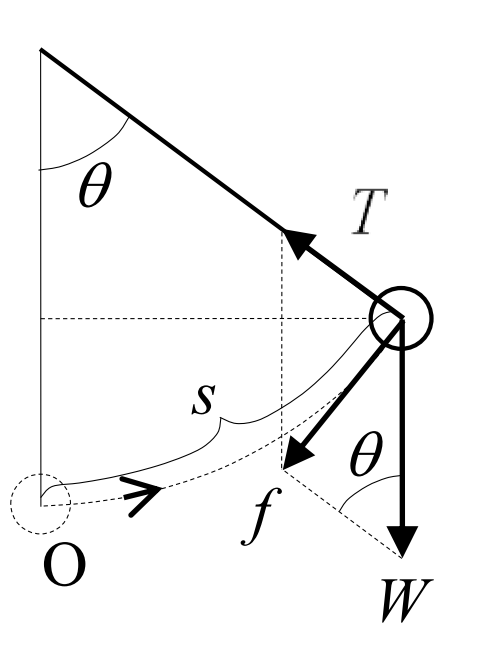糸の張力$\,T\,$、重力$\,W\,$の合力$\,f^{\prime\prime}$が重りに掛かる。
$\quad W=mg$
$\quad f^{\prime\prime}=mg\sin\theta$
円周方向の重りの動く長さを$\,s\,$とすると
$\quad m\dfrac{d^2s}{dt^2}=-mg\sin\theta$
$\quad s=l\theta\,$なので$\quad\dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\sin\theta$
振幅が小さいときは
$\quad\theta\approx\sin\theta\quad$とすることが出来るので
$\quad\dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\theta\quad$とすることが出来、次のような一般解が得られる。

$\quad\theta=A\sin\sqrt{\dfrac{g}{l}}t+B\cos\sqrt{\dfrac{g}{l}}t$
ここで初期条件として$\quad t=0\quad d\theta/dt=0\quad\theta=\theta_0\quad$とすると
$\quad\theta=\theta_0\cos\sqrt{\dfrac{g}{l}}t\quad$が得られる。
周波数$\,f\,$は$\quad f=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}\quad$となる。
周期$\,T\,$は$\quad T=\dfrac{1}{f}=2\pi\sqrt{\dfrac{l}{g}}\quad$である。

今回は紐の長さを$\,30\,$cm としたので、

$\quad T=2\times 3.141593\times\sqrt{\dfrac{0.3}{9.80655}}=1.099..\,$(s) となった。結果のグラフを見ると、振れ角$20\,$度以下ではほぼこの周期となっているようである。

5.検討2：振幅が大きい場合

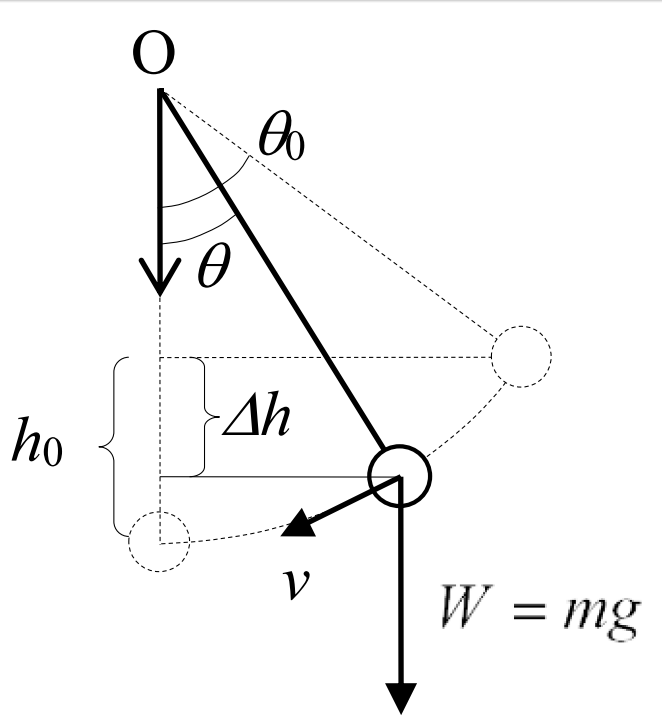エネルギー保存則を用いて、振幅の大きい振り子の運動を計算する。振り子の最下点を原点とし、振りだし高さを$\,h_0\,$、$\Delta h\,$だけ降りた点の円周方向の速度を$\,v\,$とすると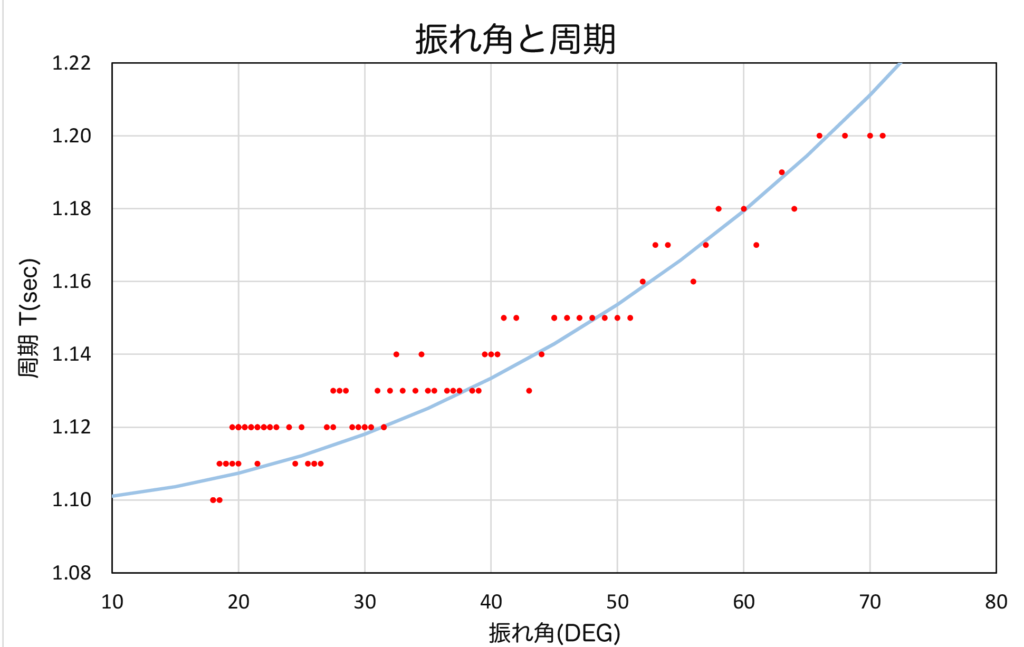
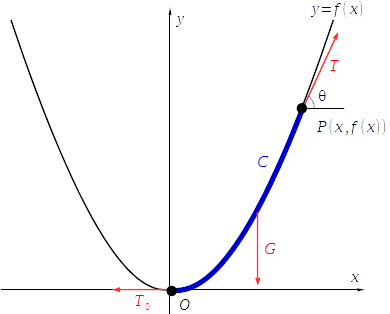$\quad\dfrac{1}{2}mv^2=mgl(\cos\theta-\cos\theta_0)\quad$なので
$\quad\therefore v=\sqrt{2gl(\cos\theta-\cos\theta_0)}$
ここで、$\,v=\dfrac{ds}{dt}=l\dfrac{d\theta}{dt}\quad$なので
$\quad l\dfrac{d\theta}{dt}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad$より
$\quad dt=\sqrt{\dfrac{l}{2g}}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}$

これを積分すると周期を求めることが出来る。
$\,t\,$の積分範囲を$\,4\,$分の$\,1\,$周期とすると、$\theta=0\,\to\,\theta_0$
$\displaystyle\int^{\frac{T}{4}}_0dt=\dfrac{T}{4}=\sqrt{\dfrac{l}{2g}}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}$

ここからの積分は振り子の計算その２を参考にしてください。

プロセスとしては$\quad\sin\phi=\sin(\theta/2)/\sin(\theta_0/2)\quad$とおいて、いくつかの計算を経て以下の積分となる。
$\quad T=4\sqrt{\dfrac{l}{g}}\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{d\phi}{\sqrt{1-\sin^2(\theta_0/2)\sin^2\phi}}$
この積分は楕円積分と呼ばれる。

5.1 楕円積分の計算

楕円積分を参照のこと。

第１種の楕円積分は以下のような式となる。

$\quad I=\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{d\phi}{\sqrt{1-a^2\sin^2\phi}}=\dfrac{\pi}{2}\displaystyle\sum_{n=0}^{\infty}\left\{\dfrac{2n-1)!!}{2n!!}\right\}^2a^{2n}$
ここで$\quad n!!\quad$は二重階乗である。

これより、$\,T\quad$は以下のようになる。
$\quad T=4\sqrt{\dfrac{l}{g}}\displaystyle\int_0^{\frac{\pi}{2}}\frac{d\phi}{\sqrt{1-\sin^2(\theta_0/2)\sin^2\phi}}$

$\qquad=2\pi\sqrt{\dfrac{l}{g}}\displaystyle\sum_{n=0}^{\infty}\left\{\dfrac{(2n-1)!!}{2n!!}\right\}^2\left(\sin\dfrac{\theta_0}{2}\right)^{2n}$

具体的な計算は$\quad b=\sin\dfrac{\theta_0}{2}\quad$とおいて、振り子の長さ$\,l=0.3\,$m を使うと

$\quad　T=2\pi\sqrt{\dfrac{l}{g}}\left\{1+\left(\dfrac{1}{2}\right)^2b^2+\left(\dfrac{1}{2}\dfrac{3}{4}\right)^2b^4+\left(\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{6}\right)^2b^6\right.$

$\qquad\qquad\qquad \left.+\left(\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{6}\dfrac{7}{8}\right)^2b^8+\left(\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{6}\dfrac{7}{8}\dfrac{9}{10}\right)^2b^{10}+\cdots\,\right\}$

$\qquad=1.099\times\left\{1+\dfrac{1}{4}b^2+\dfrac{9}{64}b^4+\dfrac{25}{256}b^6+\dfrac{1225}{16384}b^8\right.$

$\qquad\qquad\qquad\left.+\dfrac{3969}{65536}b^{10}+\dfrac{53361}{1048576}b^{12}+\cdots\,\right\}$

この値と実験結果を併せて表示する。

測定データが $\quad 1/30\,$sec 単位であるが、まあ妥当な結果となったようである。

懸垂線

ひもの両端を持って垂らしたときにできる曲線を懸垂曲線( カテナリー catenary )といいますが、この曲線の方程式を導いてみる。

ひもの底を原点$O\,$とし、水平方向に$x\,$軸、鉛直方向に$y\,$軸をとる。ひもの曲線を$\,y=f(x)\,$とおいて関数$\,f(x)\,$を求める。

ひもの$\,x>0\,$の部分に点$\,(x,f(x))\,$をとり、これを$P\,$とします。また、ひもの$O\,$から$P\,$の部分(両端を含む)を$C\,$とします。

【$\,f(x)\,$に対する微分方程式を立てる】

ひもの一部$\,C\,$に加わる力の釣り合いの式から$\,f(x)\,$についての微分方程式を立てる。$C\,$には次の３つの力が加わっている。

点$\,O\,$に水平方向のひもの張力$\,T_0$
点$\,P\,$に接線方向上向きにひもの張力$\,T$
$\,C\,$の重心に鉛直下向きに重力$\,G$

ここで、原点にはたらく張力$\,T_0\,$は$\,x\,$に関係なく一定なので定数とする。

$T\,$について、$P\,$における$\,f(x)\,$の接線と$\,x\,$軸の正の部分とのなす角を$\,\theta\,$とすると、$T\,$の$\,x\,$成分、$y\,$成分はそれぞれ$\,T\cos\theta\,,\,T\sin\theta\,$となる。

この角度$\,\theta\,$と$\,f(x)\,$は、$x\,$における微分が接線なので
$\quad f'(x)=\tan\theta\quad$となる。

$C\,$の長さを$\,l\,$とすると曲線の長さの式から
$\quad l=\displaystyle\int_0^x\sqrt{1+\{f'(x)\}^2}dx\quad$で求められる。

線密度を$\,\rho\,$、重力加速度を$\,g\,$とすると
$\quad G=\rho lg=\rho g\quad$となる。

これらより釣り合いの式は以下のようになる。

鉛直方向：$\,T\sin\theta=\rho lg$
水平方向：$\,T\cos\theta=T_0$

$T\,$を消去して、定数をまとめて $\,k=\dfrac{\rho g}{T_0}\,\,$とおくと

$\quad f'(x)=k\displaystyle\int_0^x\sqrt{1+\{f'(x)\}^2}dx\quad$となる。

両辺を$\,x\,$で微分すると

$\quad f^{\prime\prime}(x)=k\sqrt{1+\{f'(x)\}^2}\quad$となる。

境界条件は$\quad f(0)=0\,\,,\quad f'(0)=0\quad$となる。

【微分方程式を解く】

この微分方程式を解く。$\quad z=f'(x)\quad$とおくと

$\quad\dfrac{dz}{dx}=k\sqrt{1+z^2}$
$\quad\dfrac{dz}{\sqrt{1+z^2}}=k\,dx\quad$となる。

先程の条件で$\quad f'(x)=\tan\theta=z\quad$なので
$\quad dz=\dfrac{1}{\cos^2\theta}d\theta\quad$となる。よって、

$\quad \dfrac{dz}{\sqrt{1+z^2}}=\dfrac{1}{\sqrt{1+\tan^2\theta}}\dfrac{d\theta}{\cos^2\theta}=\dfrac{d\theta}{\sqrt{\dfrac{\cos^2\theta+\sin^2\theta}{\cos^2\theta}}\cos^2\theta}$
$\qquad =\dfrac{d\theta}{\cos\theta}\quad$となる。

このままでは積分出来ないので、$\quad\dfrac{d}{d\theta}\sin\theta=\cos\theta\quad$を利用して

$\quad\dfrac{d\theta}{\cos\theta}=\dfrac{d(\sin\theta)}{\cos^2\theta}=\dfrac{d(\sin\theta)}{(1-\sin\theta)(1+\sin\theta)}$

$\quad =\dfrac{1}{2}\left(\dfrac{1}{1-\sin\theta}+\dfrac{1}{1+\sin\theta}\right)\,d(\sin\theta)\quad$となる。

この形なら積分可能なので$\,\,\sin\theta\,\,$で積分する。

$\quad\displaystyle\int\dfrac{dz}{\sqrt{1+z^2}}=\dfrac{1}{2}\displaystyle\int\left(\dfrac{1}{1-\sin\theta}+\dfrac{1}{1+\sin\theta}\right)\,d(\sin\theta)$

$\quad=\dfrac{1}{2}\left\{-\log(1-\sin\theta)+\log(1+\sin\theta)\right\}$

$\quad=\dfrac{1}{2}\log\left(\dfrac{1+\sin\theta}{1-\sin\theta}\right)$

よって$\quad z=\tan\theta\quad$として

$\quad f'(x)=\displaystyle\int\dfrac{dz}{\sqrt{1+z^2}}=\dfrac{1}{2}\log\left(\dfrac{1+\sin\theta}{1-\sin\theta}\right)=kx+C_1\quad$ となる。

境界条件$\quad f'(x)=0\quad x=0\,\,,\,\theta=0\quad$より$\quad C_1=0\,\,$。

$\quad\dfrac{1+\sin\theta}{1-\sin\theta}=e^{2kx}\quad$より、まず$\quad\sin\theta\quad$について解く。

$\quad 1+\sin\theta=e^{2kx}(1-\sin\theta)\qquad (e^{2kx}+1)\sin\theta=e^{2kx}-1$

$\quad \sin\theta=\dfrac{e^{2kx}-1}{2^{2kx}+1}\quad$となる。ここから以下の公式を使う。

$\quad 1+\dfrac{1}{\tan^2\theta}=\dfrac{\tan^2\theta+1}{\tan^2\theta}=\dfrac{\sin^2\theta+\cos^2\theta}{\sin^2\theta}=\dfrac{1}{\sin^2\theta}$

$\quad\dfrac{1}{\tan^2\theta}=\left(\dfrac{e^{2kx}+1}{2^{2kx}-1}\right)^2-1$

$\qquad=\dfrac{(e^{2kx}+1)^2-(e^{2kx}-1)^2}{(e^{2kx}-1)^2}$

$\qquad=\dfrac{4e^{2kx}}{(e^{2kx}-1)^2}\quad$より

$\quad\tan\theta=\dfrac{e^{2kx}-1}{2e^{kx}}=\dfrac{e^{kx}-e^{-kx}}{2}=\sinh kx$

$\quad f'(x)=z=\tan\theta=\sinh kx\quad$なので

$\quad f(x)=\displaystyle\int\dfrac{e^{kx}-e^{-kx}}{2}dx=\dfrac{e^{kx}+e^{-kx}}{2k}+C_2$

境界条件が$\quad f(0)=0\quad$なので$\quad C_2=-k\quad$より

$\quad f(x)=\dfrac{e^{kx}+e^{-kx}}{2k}-k=\dfrac{\cosh kx-1}{k}$

ちょっと勉強を

放送大学での天文での研究として、恒星について報告書（修論）を出したんですが、結果が中途半端でした。連星での質量のやりとりをH$\alpha$線のスペクトルを観測して調べようというものです。近接連星なので片方（質量の小さい）から大量の水素が流れ込んでいます。水素の温度は1万$^{\circ}$Kを超えており、もう片方の星に落ちるときはそのエネルギーで、H$\alpha$線のスペクトルが輝線または吸収線として現れます。
表面近くからスペクトル線が観測されると予想していたら、両方の共通重心の位置からしか観測されません。これを少しでも理解するためには、物理の知識が必要です。
高温なので当然、プラズマになっているので形としては「電磁流体解析」となるようです。まずは、流体力学を勉強しないとということで、入門書から始めます。
テキストとして、日本機械学会のJSMEシリーズの「流体力学」用います。

ポリトロープその２

天文においてポリトロープとは、圧力と密度がポリトロピック関係を満たし力学平衡にある球対称な流体である。
一般に、圧力$\,P\,$と密度$\,\rho\,$の間に
$\quad P=K\rho^{1+\frac{1}{N}}\quad\cdots\,$ (1)
の関係があるとき、この関係式をポリトロピックと呼ぶ。ここで$\,N\,$はポリトロピック指数、$\,K\,$は比例定数である。
熱力学では $\,1+\dfrac{1}{N}=\gamma\,$ であるが、天文では後述の Lane-Emden 方程式の解法のために、この形の表記を行う。
また、断熱圧縮率($\,\Gamma_1\,$)を以下のような形で表す。
$\quad\Gamma_1\equiv\,\left(\dfrac{\partial\ln P}{\partial\ln\rho}\right)_S=\left(\dfrac{\partial\ln P}{\partial\ln\rho}\right)_T\gamma\quad\cdots\,$ (2)
理想気体の場合$\, (\partial\ln P/\partial\ln\rho)_T=1\,$となるので、
$\quad\Gamma_1=\gamma\equiv\,\dfrac{C_P}{C_V}\quad\cdots\,$ (3)
ポリトロピック指数と星の種類
・$N=0\,$：密度一定のガス
・$N=0.5\sim 1\,$：中性子星
・$N=\frac{3}{2}\,$：非相対論的ガス球　白色矮星、ガス惑星　RGの核
・$N=3\sim3.5\,$：相対論的ガス　放射優勢の太陽などの恒星
・$N=5\,$：半径が無限大の星
・$N=\infty\,$：等温のガス球

［1］状態方程式
粒子がエネルギー$\,\epsilon\,$、化学ポテンシャル$\,\mu\,$に存在する確率は分布関数
$\quad f(\epsilon)=\dfrac{1}{\exp[(\epsilon-\mu)/k_BT]\pm1}\quad\cdots$(4)
符号$\,\pm\,$は+がフェルミ粒子、-がボース粒子に対応する。
高温あるいは低密度で粒子の存在期待値が小さい場合、量子力学の効果が無視出来て
$\quad f(\epsilon)=e^{\mu/k_BT}\,e^{-\epsilon/k_BT}\,$と近似出来る。
マックスウェル・ボルツマン分布が成り立つ条件は$\,e^{\mu/k_BT}\ll1\,(\mu<0\,)\,$であり、理想気体の状態方程式が数密度が以下を充たす場合である。$A_m\,$を粒子当たりの平均分子量とすると
$\quad n=\dfrac{\rho}{A_mM_u}\ll\dfrac{g(2\pi mk_BT)^{3/2}}{h^3}\quad\cdots\,$(5)

［2］光子ガス
光子はスピン1のボース粒子でボース-アインシュタイン統計に従う。エネルギーを$\epsilon$とすると、$\epsilon=pc\,,\quad v=c\,$で統計的重みは$\,g=2$、光子数は保存されないので$\mu=0$である。これより放射の圧力とエネルギー密度は
$\quad U_r=3P_r=aT^4\quad\cdots\,$ (6)　ステファンボルツマンの式
放射の圧力($P_r$)の寄与の比を $\,1-\beta\equiv P_r/P\,$と表し、気体の比熱比を$\,\gamma\,$とすると、断熱指数は
$\quad\Gamma_1=\dfrac{4}{3}+\dfrac{\beta(4-3\beta)(3\gamma-4)}{3\beta+36(\gamma-1)(1-\beta)}\quad\cdots\,$(7)
と表せる。ガス圧が優勢の$\,\beta=1\,$の時は$\,\Gamma_1=\gamma\,$で、
放射優勢の極限$\,\beta\to 0\,$で$\,\Gamma_1=4/3\,$となる。

［3］電子縮退気体
化学ポテンシャル$\,\mu\,$と熱エネルギー$\,k_BT\,$との比として縮退パラメーター$\,\Phi\,$を定義する
$\quad\Phi=\mu/k_BT\quad\cdots\,$(8)
(5)式より縮退による理想気体からのズレは$\,\Phi\simeq 0\,$で現れるが、低温・高密度で$\,\Phi\to\infty\,$の極限で分布関数が階段関数で近似できる場合を完全縮退という。このときの化学ポテンシャルの最大値をフェルミエネルギー$\,\epsilon_F\,$、運動量をフェルミ運動量$\,p_F\,$という。
ここでフェルミモーメント$\,p_F/m_ec=x_F\,$とおくと、電子の数密度、圧力、運動エネルギー密度はそれぞれ
$\quad n_e=\dfrac{8\pi}{h^3}\displaystyle\int_0^{p_F}\!p^2dp=\dfrac{8\pi}{3}\left(\dfrac{mc}{h}\right)^3x_F^3=Bx_F^3\quad\cdots\,$(9)
$\quad P_e=\dfrac{8\pi c}{3h^3}\displaystyle\int_0^{p_F}\!\dfrac{p^4dp}{\sqrt{p^2+m_e^2c^2}}=8A\!\displaystyle\int_0^{x_F}\!\dfrac{x^4\,dx}{\sqrt{1+x^2}}\cdots\,$(10)
$\quad U_e=\dfrac{8\pi}{h^3}\displaystyle\int_0^{p_F}(\sqrt{p^2c^2+m_e^2c^4}-m_ec^2)p^2dp$
$\qquad=\dfrac{8\pi m_e^4c^5}{h^3}\displaystyle\int_0^{x_F}\!(\sqrt{1+x^2}-1)x^2dx=Ag(x_F)\quad\cdots\,$(11)
ここで、$\,A\,,B\,$はそれぞれ
$\quad A\equiv\dfrac{\pi m_e^4c^5}{3h^3}=6.002\times10^{22}$dyn cm$^{-2}$
$\quad B\equiv\dfrac{8\pi}{3}\left(\dfrac{mc}{h}\right)^3=9.739\times10^5$g cm$^{-3}$
また
$\quad f(x)=8\displaystyle\int_0^x\!\dfrac{y^4\,dy}{\sqrt{1+y^2}}=\!x(2x^2-3)\sqrt{1+x^2}+3\sinh^{-1}x$
$\quad g(x)=24\displaystyle\int_0^x(\sqrt{1+y^2}-1)y^2\,dy$
$\qquad=3\{2x(x^2+1)^{3/2}-x\sqrt{x^2+1}-\sinh^{-1}x\}-8x^3$
$\qquad=8x^3(\sqrt{1+x^2}-1)-f(x)$
のように定義されます。
$\quad U_e=Ag(x_F)\,,\quad P_e=Af(x_F)\quad$また、
$\quad P=(\gamma-1)U\quad$ なので、電子ガスにおいて
$\quad \gamma=\dfrac{f(x_F)}{g(x_F)}+1\quad\cdots\,$(12)
と表すことが出来る。

図のように、$p_F/m_ec=x_F\ll 1\,$では、$\gamma\to 5/3\,$となり、
相対論的極限の $x_F\gg 1\,$では、$\gamma\to 4/3\,$となる。

ポリトロープその１

ポリトロープとは、熱力学で使うときと天文で使うときで多少感じが違う。まずは、熱力から

● ポリトロープ変化

圧力$ P$と比容積$ V$が以下の関係で結ばれる変化をポリトロープ変化という（この変化は可逆変化）
$\quad PV^n=C\quad n$: ポリトロープ指数
$\qquad n=0\qquad P=C\quad\,\,$: 等圧変化
$\qquad n=1\qquad PV=C\quad$: 等温変化
$\qquad n=\gamma\qquad PV^{\gamma}=C\quad$: 断熱変化
$\qquad n=\infty\quad\,\, V=C\qquad$: 等積変化

【1】気体の比熱

熱力学の第1法則は
$\,U\,$を内部エネルギー、$\,Q\,$を熱量、$\,W\,$を仕事とすると
$\quad dU=d’W+d’Q\quad \cdots$(1)
と表せる。ここで $ d’\,$は準静的過程を表す。
$\quad d’W=-PdV\quad \cdots$(2)
$\quad dU=-PdV+d’Q\quad \cdots$(3)
体積が一定として、$dT\,$で割ると
$\quad C_V=\dfrac{d’Q}{dT}=\left(\dfrac{\partial U}{\partial T}\right)_V\quad \cdots$(4)
同様に、圧力が一定とすれば
$\quad C_P=\left(\dfrac{\partial U}{\partial T}\right)_P+P\left(\dfrac{\partial V}{\partial T}\right)_P\quad \cdots$(5)

また、(4)式を $T$で積分すると$\,\,U=C_VT\quad \cdots$(6)
1モルでは $\,\,PV=\mathrm{R}T\quad \cdots$(7)$\,\,$で
$\quad P\left(\dfrac{\partial V}{\partial T}\right)_P=\mathrm{R}\quad \cdots$(8)　なので、(5)式は
$\quad C_P=C_V+\mathrm{R}\quad \cdots $(9)

【2】断熱変化

$dU\,$の微分を考える
$\quad dU=\left(\dfrac{\partial U}{\partial T}\right)_VdT+\left(\dfrac{\partial U}{\partial V}\right)_TdV\quad \cdots$(10)
これを(3)式に代入すると
$\quad d’Q=\left(\dfrac{\partial U}{\partial T}\right)_VdT+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]dV\quad \cdots$(11)
$P=$一定として(11)式を$dT\,$で割ると
$\quad C_P=C_V+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]\left(\dfrac{\partial V}{\partial T}\right)_P\quad \cdots$(12)
断熱変化では $d’Q=0\,$なので(11)式は
$\quad \left(\dfrac{\partial U}{\partial T}\right)_VdT+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]dV=0\quad \cdots$(13)
理想気体では$\,(U\,$は温度だけの関数なので $\left(\dfrac{\partial U}{\partial V}\right)_T=0$
(13)式に(6)式と(7)式を代入すると
$\quad C_VdT+\dfrac{\mathrm{R}T}{V}dV=0\quad \cdots$(14)
比熱比を$\,\gamma=\dfrac{C_P}{C_V}\quad \cdots$(15)$\quad$として(14)式を$C_VT\,$で割ると
$\quad \dfrac{dT}{T}+(\gamma-1)\dfrac{dV}{V}=0\quad \cdots$(16)$\quad$なので
$\quad \ln T+(\gamma-1)\ln V= \text{一定} \cdots$(17)$\quad$よって
$\quad TV^{\gamma-1}= \text{一定} \cdots$(18)
式(7)より$\quad T=\dfrac{PV}{\mathrm{R}}\quad\cdots$(19)を代入すると
$\quad PV^{\gamma}=\text{一定}\quad \cdots$(20)「ポアソンの法則」が得られる。
常温での$\,C_V\,$は並進運動と回転運動の自由度の$\frac{\mathrm{R}}{2}\,$倍となる。
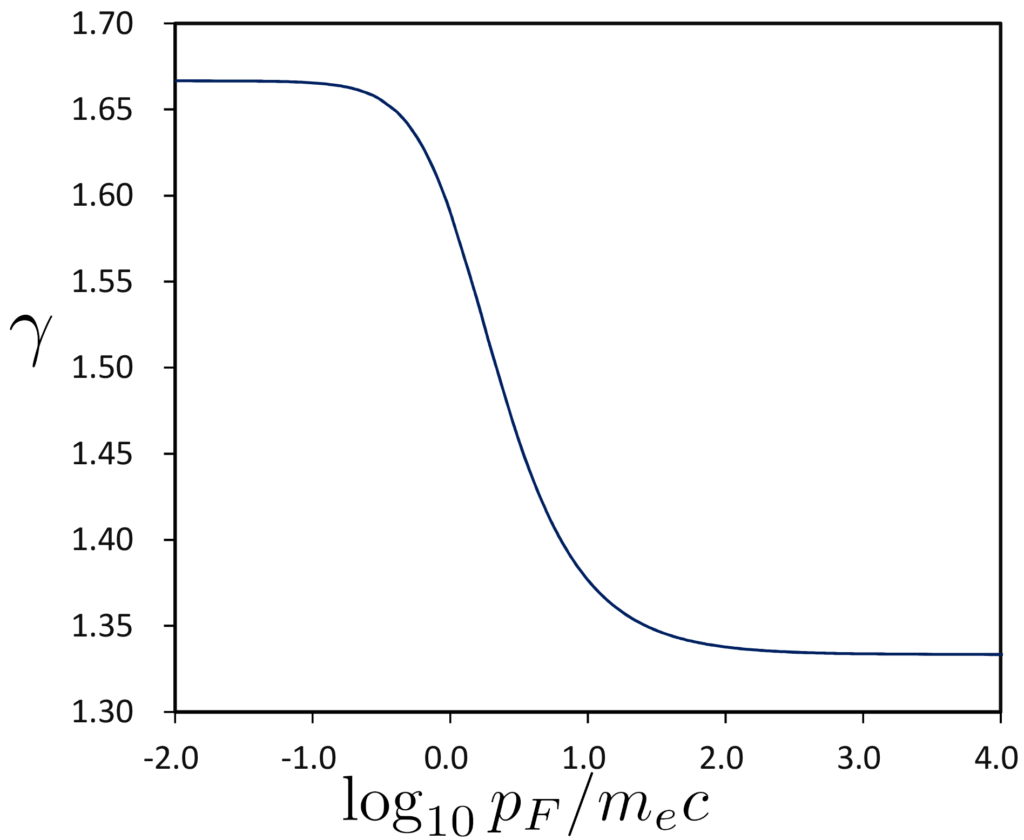
単原子分子では並進運動の自由度が３なので、$\,C_V=\frac{3}{2}\mathrm{R}$。
２原子分子では$\theta\,,\,\phi\,$の回転が加わり、自由度が５になるので、$\,C_V=\frac{5}{2}\mathrm{R}$となる。
３原子分子(直線形)では、並進の自由度と回転の自由度は、２原子分子と同様だが振動の自由度が4となる。この振動は常温での比熱に寄与しないので、$\,C_V\,$は同じとなる。
よって、単原子分子は $\gamma=\frac{5}{3}\,$となり、２原子分子と直線形の３原子分子は $\,\gamma=\frac{7}{5}\,$となる。

振り子の計算（その2）

エネルギー保存の法則から振り子の周期 $T$ の式を求める。
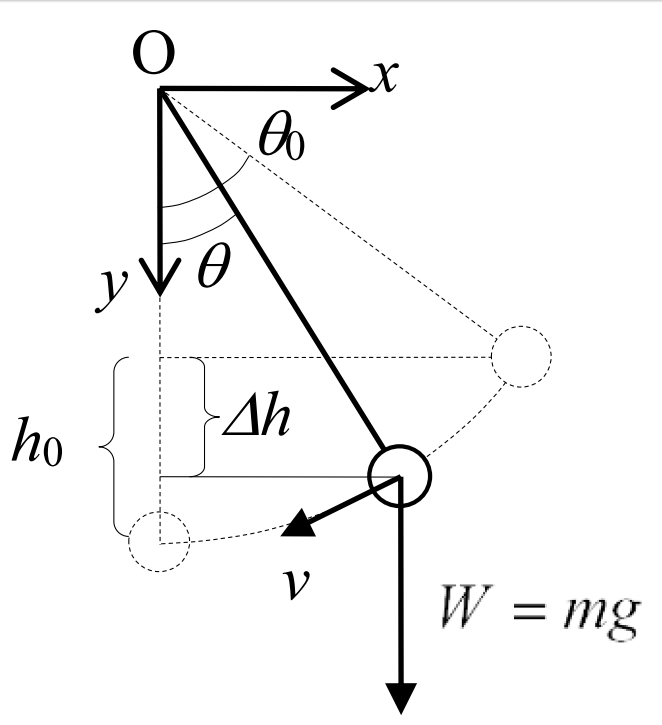振り子の支点より水平方向に $\ x\ $軸をとり、鉛直方向に $\ y\ $軸をとると、エネルギー保存則から、次式が成立する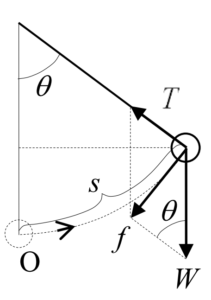

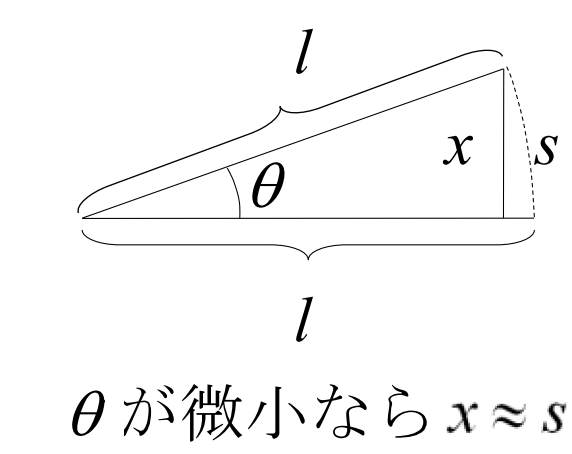$ \dfrac{1}{2}mv^2=mg\Delta h\quad$ (21)

ここで、$\ v\ $は重りが円周方向に移動する速度で、$\Delta h\ $は重りの落下距離である。ここで

$\Delta h=l\cos\theta-l\cos\theta_0=l\ (\cos\theta-\cos\theta_0)\quad$ (22)
なので

$ \dfrac{1}{2}mv^2=mgl(\cos\theta-\cos\theta_0)$
$ \therefore \ v=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad$ (23)

さらに

$ v=\dfrac{ds}{dt}=l\dfrac{d\theta}{dt}\quad$ (24)

なので、以下の式が得られる。

$ l\dfrac{d\theta}{dt}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad$(25)

$ dt=\dfrac{1}{\sqrt{2}\omega}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad$ (26)

$\quad\because\,\,\omega:=\sqrt{\dfrac{g}{l}}$

この(26)式を積分すると周期を求めることが出来る。積分範囲を4分の1周に相当する $\ t=T/4\ $とすると、右辺の積分範囲は$\ \theta=0\sim\theta_0\ $となるので、

$ \displaystyle\int_0^{\frac{T}{4}}dt=\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad$ (27)

$\therefore\,\, T=4\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad$ (28)

この積分を行うために、半角公式を使って以下の変換を行う

$ \cos\theta=1-2\sin^2\frac{\theta}{2}\quad\cos\theta_0=1-2\sin^2\frac{\theta_0}{2}$

ここで $\,\,k:=\sin\frac{\theta_0}{2}\quad \sin\phi:=\sin\frac{\theta}{2}/k\,\,$とすると

$ \cos\theta-\cos\theta_0=1-2\sin^2\frac{\theta}{2}-\left(1-2\sin^2\frac{\theta_0}{2}\right)$

$\quad=2\left(\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}\right)=2k^2\cos^2\phi\,\,$となる

$k\sin\phi=\sin\frac{\theta}{2}\,\,$を両辺微分して$\,\,k\cos\phi\,d\phi=\frac{1}{2}\cos\frac{\theta}{2}\,d\theta$

$d\theta=\dfrac{2k\cos\phi\,d\phi}{\cos\frac{\theta}{2}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-\sin^2\frac{\theta}{2}}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}$

なので

$\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}=\dfrac{1}{\sqrt{2}k\cos\phi}\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}$

$\quad=\dfrac{\sqrt{2}\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\,\,$となり、第１種楕円積分の形になる。

振り子の計算（その１）

［１］運動方程式

振り子には、図のような力が働く。ここで重力は$ \ W=mg\ $で糸の張力は$\ \ T=W\cos\theta\ $ である。

$W\ $と$\ T\ $の合力$\ f\ $の向きは図のように半径$\ l\ $の円周の接線方向となり、その大きさは

$f=W\sin\theta=mg\sin\theta$　(1)

である。この合力$\ f\ $により、重りは円弧を描くように往復運動をする。ここで、運動を円軌道として考えるために、振り子の釣り合いの位置 O から、円弧に沿って$\ s\ $軸をとる。この合力$\ f\ $は重りを$\ s\ $軸の負の方向に運動させる力となるため、重りの運動方程式は

$ m\dfrac{d^2s}{dt^2}=-f=-mg\sin\theta\ $　(2)

すなわち

$ \dfrac{d^2s}{dt^2}=-g\sin\theta\ $　(3)

と表すことが出来る。　円弧の長さは $\ s=l\ \theta\ $で表せられ、２回微分は

$\ \dfrac{d^2s}{dt^2}=l\dfrac{d^2\theta}{dt^2}\ $　(4)

となるので、運動方程式は重りの角度$\ \theta\ $に対して

$ \dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\sin\theta\ $　(5)

と表すことが出来る。

［２］運動方程式の近似解

　(5)式の運動方程式は、三角関数を含んでいるため、このままでは階を求めることが難しい。但し、円弧の角度$\ \theta\ $が微少の場合、三角形の高さ$\ x=\sin\theta\ $は円弧の長さ$\ s\ $にほぼ等しくなり
$\quad x\ \approx\ s\ $とおけるため

$ \sin\theta=\dfrac{x}{l}\ \approx\ \dfrac{s}{l}=\dfrac{l\theta}{l}=\theta\ $　(6)

となり、運動方程式は

$ \dfrac{d^2\theta}{dt^2}=-\omega^2\theta\qquad \omega:=\sqrt{\dfrac{g}{l}}\quad$ (7)

と表すことが出来る。これは単振動で良く近似出来る。一般解は

$ \theta=A\sin\omega t+B\cos\omega t $　(8)

ここで、 $ t=0\ $で$\ \theta=\theta_0\ $として、(8)式に代入すると

$ \theta_0=A\sin\omega\times 0+B\cos\omega\times 0=B\quad\therefore B=\theta_0$

つぎに、(8)式を $t$ で微分して、$\ t=0\ $で$\ \dfrac{d\theta}{dt}=0\ $ とすると

$ \dfrac{d\theta}{dt}=A\omega\cos\omega t-B\omega\sin\omega t$

$\qquad =A\omega\cos\omega\times 0-B\omega\sin\omega\times 0=A\omega=0 $

よって、$\ A=0\ $となり、(8)式は$\quad\theta=\theta_0\cos\omega t\ $ (9)

と決定される。このように解が周期関数で表される振動を単振動といい、単振動で近似出来る振り子を単振り子といいます。

$\ \omega=\sqrt{\cfrac{g}{l}}\ $ は角振動数 [rad/s] と呼ばれる。

角振動数$\ \omega\ $を 2$\pi$ で割った値は、重りが1秒間に往復する回数を表し、振動数 $\ f\ $[Hz}と呼ばれています。

$ f=\dfrac{\omega}{2\pi}=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}\ \,\,$ Hz$\quad$(10)

重りが一往復するのに必要な時間は、周期 $T$ [s] といい、振動数の逆数になる。

$T=\dfrac{1}{f}=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{l}{g}}\quad$(11)

2025年7月
月	火	水	木	金	土	日
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31