［１］Lane Emden 方程式とは

・宇宙物理学や流体力学において、レーン＝エムデン方程式（Lane-Emden equation）は、球対称な密度分布を示す力学平衡にある自己重力流体を記述する微分方程式である。名称は宇宙物理学者のジョナサン・ホーマー・レーンとロバート・エムデンに由来する。
・Jonathan Homer Lane(1819-1880,ニューヨーク州のゲネシー生まれ)エール大学でオルムステッド（Denison Olmsted）に師事し、数学と自然科学を学ぶ。1857 年にワシントン市内に特許事務所を開き、特許関係の顧問や特許弁護士などの業務を始めた。1860 年に南北戦争が勃発すると、ペンシルバニア州北部の兄弟の住む村に移り、冷却用ガス膨張装置を用いた極低温装置の開発や天文学にも興味をもち、ひとりで文献に当たりながら太陽内部構造の研究に思いを深めていた。
・太陽の進化についてはジョン・ハーシェルやケルビン卿の収縮説に興味をもっていたが、内部構造を数学的に扱っていない点がレーンには不満であった。そこで彼は太陽をガス球と仮定し、重力平衡と熱力学過程を基本にして内部構造に関する基本方程式を書き始めた。
「太陽の理論的温度」(Lane,J.H.1870,Amer.J.Sci.&Arts,50,57-74) 自己重力のもとで球状に保たれるガス体の全体的平衡状態を取り扱った歴史的論文である。彼は太陽内部を完全気体と仮定したが、これは大胆な発想であった。完全気体を考えると\(\,p=R\rho T\)、静力学的平衡は\(\,dp=-\dfrac{Gm(r)}{r^2}\rho\,dr\,\)、内部は断熱的に対流平衡となるので、内部構造は\(\,1-\left(\dfrac{\rho}{\rho_c}\right)^{\gamma-1}=\displaystyle\int_0^x\dfrac{\mu(x)}{x^2}dx\,\)にて与えられる。

［２］アウグスト・リターのガス球論

・August Ritter(1826-1908)1853年にゲッチンゲン大学卒業。アーヘン工業大学(現RWTH-Aachen)の構造力学と一般力学の担当教授。「大気の高さに関する考察とガス状天体の内部構造について」ガス球の平衡・振動・安定性の問題に取り組み、自己重力にあるポリトロープガス球の平衡状態についての先駆的研究。
・ポリトロープとは圧力と密度に\(\,pV^n=K\,\) または\(\,p=K\rho^{1+1/n}\,\)の関係を満たす過程のこと。
\(\,T/T_c=y\,,\quad r/a=x\,\)とおいて、重力平衡式と組み合わせると以下の基本微分方程式が得られる。
\(\quad\dfrac{d^2y}{dx^2}+\dfrac{2}{x}\dfrac{dy}{dx}+y^n=0\,\quad\cdots\,\)(1)
この式は ポリトロープガス球の内部構造に関する基本方程式として、エムデンやエディントンに大きな影響を与えた。

［３］エムデンのガス球論

・ロベルト・エムデン(Jacob Robert Emden,1862-1940)スイスの天体物理学および気象学の専門家。1907 年にミュンヘン工科大学の教授。「ガス球論」出版。リターの基本方程式もそのままの形で再度導かれており、通常、エムデンの微分方程式と呼ばれている。リターらと異なり、エムデンはガス球半径を有限の場合と無限の場合を併行して考察している。エムデンの基本的考え方はレーンやリターと変わっていないが、理論が整備され、応用例が多いことからガス球理論の集大成と呼ばれ、4 版を重ねて、星の内部構造論の基本的テキストとなって広く知られるようになった。なお、エムデンの甥、マーチン・シュワルツシルドは 1958 に著書「星の構造と進化｣を著わしているが、この書で歴史的なマイルストーンの研究者として、順にエムデン、エディントン、チャンドラセカールの 3 人の名前を挙げている。

［４］星の力学的安定

・連続の式:
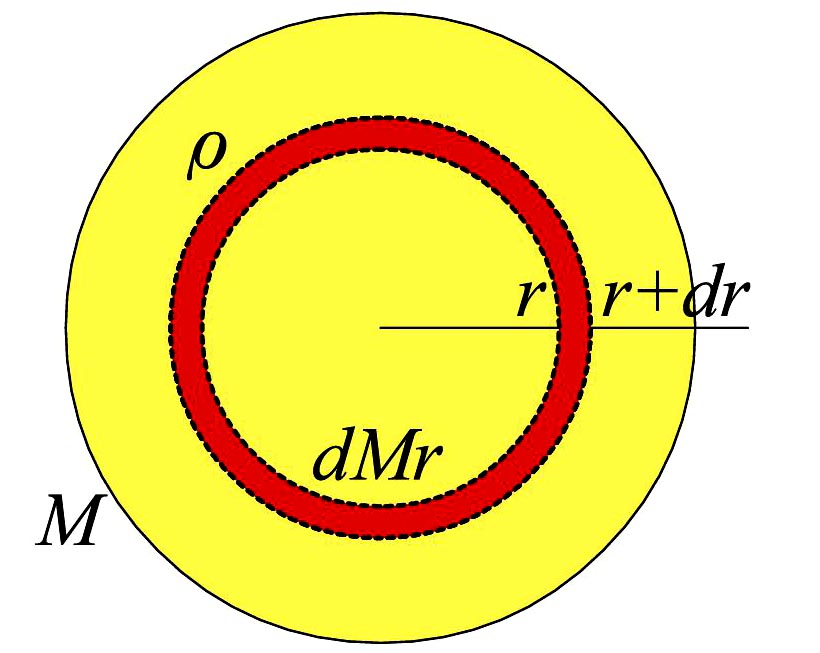　半径\(\,r\,\)、ガス密度は半径の関数とし、\(\,\rho(r)\,\) と表すと、その半径より内側に含まれる質量\(\,M_r\,\)は
\(\quad M_r=\displaystyle\int_0^r4\pi r’^2\rho(r)dr’\quad\cdots\,\)(2)
と書くことができる。
この式の両辺を\(\,r\,\)で微分して微分形式で書き表すと
\(\quad\dfrac{dM_r}{dr}=4\pi r^2\rho(r)\quad\cdots\,\)(3)
となる。この式は流体力学の連続の式(continuity equation)の一種である。

・静水圧平衡:
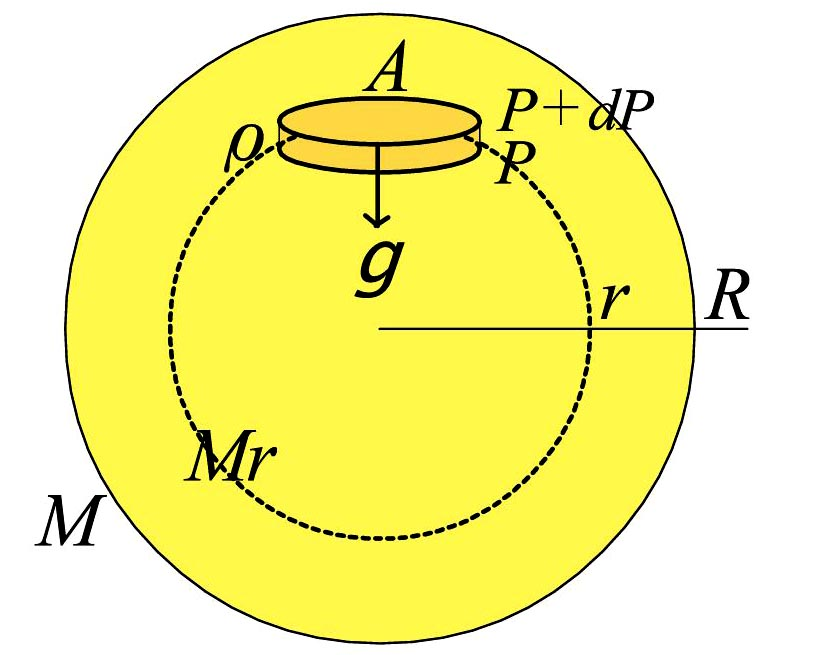　星は自分自身の重力による収縮しようとする力とガス圧による対抗する力がバランスして、力学平衡を保っている。
\(\,r\,\)を中心からの距離、\(\,P\,\)をそこでの圧力、\(\,G\,\)を重力定数として
\(\quad\dfrac{dP}{dr}=-\dfrac{GM_r}{r^2}\rho\quad\cdots\,\)(4)
と表せる。
連続の式(3)、静水圧平衡の式(4)を解くことで、天体の内部構造を明らかにすることができる。 しかしこの段階では、独立変数が半径\(\,r\,\)で、従属変数は密度\(\,\rho\)、圧力\(\,P\)、質量\(\,M_r\,\)の３つで方程式は２つしかない。ためもうひとつ変数を結びつける式が必要となる。

・ポリトロープ関係
ここで、前出のポリトロープ関係と呼ばれる関係式を導入する。
\(\quad P=K\rho^{1+\frac{1}{N}}\quad\cdots\,\)(5)
\(\,K\,,\,\,N\,\)は定数のパラメータであり、\(\,N\,\)のことをポリトロープ指数と呼ぶ。

［５］レーン=エムデン方程式の導出

天体内部の構造を決めるためには、式(3)、(4)、(5)を解けば良いことになる。まず式(4)から
\(\quad\dfrac{r^2}{\rho}\dfrac{dP}{dr}=-GM_r\quad\cdots\,\)(6)
となり、両辺を\(\,r\,\)で微分すると
\(\quad\dfrac{d}{dr}\left(\dfrac{r^2}{\rho}\dfrac{dP}{dr}\right)=-G\dfrac{dM_r}{dr}\quad\cdots\,\)(7)
となる。これを式(3)に代入すると
\(\quad\dfrac{d}{dr}\left(\dfrac{r^2}{\rho}\dfrac{dP}{dr}\right)=-4\pi Gr^2\rho\quad\cdots\,\)(8)
となる。また、式(5)を\(\,r\,\)で微分すると
\(\quad\dfrac{dP}{dr}=K\left(1+\dfrac{1}{N}\right)\rho^{\frac{1}{N}}\dfrac{d\rho}{dr}\quad\cdots\,\)(9)
が得られる。式(9)を式(8)に代入すると
\(\quad K\left(1+\dfrac{1}{N}\right)\dfrac{d}{dr}\left(r^2\rho^{\frac{1}{N}-1}\dfrac{d\rho}{dr}\right)=-4\pi Gr^2\rho\quad\cdots\,\)(10)

ここで密度\(\,\rho(r)\,\)を星の中心密度\(\,\rho_c\,\)として
\(\quad\rho=\rho_c\theta^N\quad\cdots\,\)(11)
の形で表すこととする。\(\theta\,\)は無次元化した密度。
両辺を\(\,r\,\)で微分すると
\(\quad\dfrac{d\rho}{dr}=\dfrac{d}{dr}\left(\rho_c\theta^N\right)=\rho_cN\theta^{N-1}\dfrac{d\theta}{dr}\quad\cdots\,\)(12)
また、式(11)から以下の関係が導かれる
\(\quad\rho^{\frac{1}{N}-1}=\rho_c^{\frac{1}{N}-1}\,\theta^{1-N}\quad\cdots\,\)(13)

式(10)に式(12)(13)を代入すると
\(\quad K\left(1+\dfrac{1}{N}\right)\dfrac{d}{dr}\left(r^2\rho_c^{\frac{1}{N}-1}\theta^{1-N}\rho_cN\theta^{N-1}\dfrac{d\theta}{dr}\right)\!=\!-4\pi Gr^2\rho_c\theta^N\quad\)
\(\quad\dfrac{K(N+1)\rho_c^{\frac{1}{N}-1}}{4\pi G}\dfrac{1}{r^2}\dfrac{d}{dr}\left(r^2\dfrac{d\theta}{dr}\right)=-\theta^N\quad\cdots\,\)(14)

また式(5)を星の中心にあてはめると
\(\quad P_c=K\rho_c^{1+\frac{1}{N}}\quad\cdots\,\)(15)
この式(15)を式(14)に代入して\(\,K\,\)を消去すると
\(\quad\dfrac{(N+1)P_c}{4\pi G\rho_c^2}\dfrac{1}{r^2}\dfrac{d}{dr}\left(r^2\dfrac{d\theta}{dr}\right)=-\theta^N\quad\cdots\,\)(16)

左辺の係数部分を以下のように定義すると
\(\quad\alpha\equiv\left[\dfrac{(N+1)K}{4\pi G}\rho_c^{\frac{1}{N}-1}\right]^{1/2}\quad\cdots\,\)(17)
\(\quad\dfrac{\alpha^2}{r^2}\dfrac{d}{dr}\left(r^2\dfrac{d\theta}{dr}\right)=-\theta^N\quad\quad\cdots\,\)(18)

ここで、半径を以下の形に無次元化する。
\(\quad\xi=\dfrac{r}{\alpha}\quad\cdots\,\)(19)
これより無次元化した密度\(\,\theta\,\)の\(\,r\,\)の微分は以下のようになる
\(\quad\dfrac{d\theta}{dr}=\dfrac{d\theta}{d\xi}\dfrac{d\xi}{dr}=\dfrac{1}{\alpha}\dfrac{d\theta}{d\xi}\quad\cdots\,\)(20)

微分演算子は以下の形になる
\(\quad\dfrac{d}{dr}=\dfrac{1}{\alpha}\dfrac{d}{d\xi}\quad\cdots\,\)(21)

式(18)にこれらを用いると
\(\quad\dfrac{1}{\xi^2}\dfrac{d}{d\xi}\left(\xi^2\dfrac{d\theta}{d\xi}\right)=-\theta^N\quad\cdots\,\)(22)
この式は無次元化した密度\(\,\theta\)、無次元化した半径\(\,\xi\,\)を結びつけるもので、
レーン=エムデン方程式と呼ばれている。

天文においてポリトロープとは、圧力と密度がポリトロピック関係を満たし力学平衡にある球対称な流体である。
一般に、圧力\(\,P\,\)と密度\(\,\rho\,\)の間に
\(\quad P=K\rho^{1+\frac{1}{N}}\quad\cdots\,\) (1)
の関係があるとき、この関係式をポリトロピックと呼ぶ。ここで\(\,N\,\)はポリトロピック指数、\(\,K\,\)は比例定数である。
熱力学では \(\,1+\dfrac{1}{N}=\gamma\,\) であるが、天文では後述の Lane-Emden 方程式の解法のために、この形の表記を行う。
また、断熱圧縮率(\(\,\Gamma_1\,\))を以下のような形で表す。
\(\quad\Gamma_1\equiv\,\left(\dfrac{\partial\ln P}{\partial\ln\rho}\right)_S=\left(\dfrac{\partial\ln P}{\partial\ln\rho}\right)_T\gamma\quad\cdots\,\) (2)
理想気体の場合\(\, (\partial\ln P/\partial\ln\rho)_T=1\,\)となるので、
\(\quad\Gamma_1=\gamma\equiv\,\dfrac{C_P}{C_V}\quad\cdots\,\) (3)
ポリトロピック指数と星の種類
・\(N=0\,\)：密度一定のガス
・\(N=0.5\sim 1\,\)：中性子星
・\(N=\frac{3}{2}\,\)：非相対論的ガス球　白色矮星、ガス惑星　RGの核
・\(N=3\sim3.5\,\)：相対論的ガス　放射優勢の太陽などの恒星
・\(N=5\,\)：半径が無限大の星
・\(N=\infty\,\)：等温のガス球

［1］状態方程式
粒子がエネルギー\(\,\epsilon\,\)、化学ポテンシャル\(\,\mu\,\)に存在する確率は分布関数
\(\quad f(\epsilon)=\dfrac{1}{\exp[(\epsilon-\mu)/k_BT]\pm1}\quad\cdots\)(4)
符号\(\,\pm\,\)は+がフェルミ粒子、-がボース粒子に対応する。
高温あるいは低密度で粒子の存在期待値が小さい場合、量子力学の効果が無視出来て
\(\quad f(\epsilon)=e^{\mu/k_BT}\,e^{-\epsilon/k_BT}\,\)と近似出来る。
マックスウェル・ボルツマン分布が成り立つ条件は\(\,e^{\mu/k_BT}\ll1\,(\mu<0\,)\,\)であり、理想気体の状態方程式が数密度が以下を充たす場合である。\(A_m\,\)を粒子当たりの平均分子量とすると
\(\quad n=\dfrac{\rho}{A_mM_u}\ll\dfrac{g(2\pi mk_BT)^{3/2}}{h^3}\quad\cdots\,\)(5)

［2］光子ガス
光子はスピン1のボース粒子でボース-アインシュタイン統計に従う。エネルギーを\(\epsilon\)とすると、\(\epsilon=pc\,,\quad v=c\,\)で統計的重みは\(\,g=2\)、光子数は保存されないので\(\mu=0\)である。これより放射の圧力とエネルギー密度は
\(\quad U_r=3P_r=aT^4\quad\cdots\,\) (6)　ステファンボルツマンの式
放射の圧力(\(P_r\))の寄与の比を \(\,1-\beta\equiv P_r/P\,\)と表し、気体の比熱比を\(\,\gamma\,\)とすると、断熱指数は
\(\quad\Gamma_1=\dfrac{4}{3}+\dfrac{\beta(4-3\beta)(3\gamma-4)}{3\beta+36(\gamma-1)(1-\beta)}\quad\cdots\,\)(7)
と表せる。ガス圧が優勢の\(\,\beta=1\,\)の時は\(\,\Gamma_1=\gamma\,\)で、
放射優勢の極限\(\,\beta\to 0\,\)で\(\,\Gamma_1=4/3\,\)となる。

［3］電子縮退気体
化学ポテンシャル\(\,\mu\,\)と熱エネルギー\(\,k_BT\,\)との比として縮退パラメーター\(\,\Phi\,\)を定義する
\(\quad\Phi=\mu/k_BT\quad\cdots\,\)(8)
(5)式より縮退による理想気体からのズレは\(\,\Phi\simeq 0\,\)で現れるが、低温・高密度で\(\,\Phi\to\infty\,\)の極限で分布関数が階段関数で近似できる場合を完全縮退という。このときの化学ポテンシャルの最大値をフェルミエネルギー\(\,\epsilon_F\,\)、運動量をフェルミ運動量\(\,p_F\,\)という。
ここでフェルミモーメント\(\,p_F/m_ec=x_F\,\)とおくと、電子の数密度、圧力、運動エネルギー密度はそれぞれ
\(\quad n_e=\dfrac{8\pi}{h^3}\displaystyle\int_0^{p_F}\!p^2dp=\dfrac{8\pi}{3}\left(\dfrac{mc}{h}\right)^3x_F^3=Bx_F^3\quad\cdots\,\)(9)
\(\quad P_e=\dfrac{8\pi c}{3h^3}\displaystyle\int_0^{p_F}\!\dfrac{p^4dp}{\sqrt{p^2+m_e^2c^2}}=8A\!\displaystyle\int_0^{x_F}\!\dfrac{x^4\,dx}{\sqrt{1+x^2}}\cdots\,\)(10)
\(\quad U_e=\dfrac{8\pi}{h^3}\displaystyle\int_0^{p_F}(\sqrt{p^2c^2+m_e^2c^4}-m_ec^2)p^2dp\)
\(\qquad=\dfrac{8\pi m_e^4c^5}{h^3}\displaystyle\int_0^{x_F}\!(\sqrt{1+x^2}-1)x^2dx=Ag(x_F)\quad\cdots\,\)(11)
ここで、\(\,A\,,B\,\)はそれぞれ
\(\quad A\equiv\dfrac{\pi m_e^4c^5}{3h^3}=6.002\times10^{22}\)dyn cm\(^{-2}\)
\(\quad B\equiv\dfrac{8\pi}{3}\left(\dfrac{mc}{h}\right)^3=9.739\times10^5\)g cm\(^{-3}\)
また
\(\quad f(x)=8\displaystyle\int_0^x\!\dfrac{y^4\,dy}{\sqrt{1+y^2}}=\!x(2x^2-3)\sqrt{1+x^2}+3\sinh^{-1}x\)
\(\quad g(x)=24\displaystyle\int_0^x(\sqrt{1+y^2}-1)y^2\,dy\)
\(\qquad=3\{2x(x^2+1)^{3/2}-x\sqrt{x^2+1}-\sinh^{-1}x\}-8x^3\)
\(\qquad=8x^3(\sqrt{1+x^2}-1)-f(x)\)
のように定義されます。
\(\quad U_e=Ag(x_F)\,,\quad P_e=Af(x_F)\quad\)また、
\(\quad P=(\gamma-1)U\quad\) なので、電子ガスにおいて
\(\quad \gamma=\dfrac{f(x_F)}{g(x_F)}+1\quad\cdots\,\)(12)
と表すことが出来る。

図のように、\(p_F/m_ec=x_F\ll 1\,\)では、\(\gamma\to 5/3\,\)となり、
相対論的極限の \(x_F\gg 1\,\)では、\(\gamma\to 4/3\,\)となる。

ポリトロープとは、熱力学で使うときと天文で使うときで多少感じが違う。まずは、熱力から

● ポリトロープ変化

圧力\( P\)と比容積\( V\)が以下の関係で結ばれる変化をポリトロープ変化という（この変化は可逆変化）
\(\quad PV^n=C\quad n\): ポリトロープ指数
\(\qquad n=0\qquad P=C\quad\,\,\): 等圧変化
\(\qquad n=1\qquad PV=C\quad\): 等温変化
\(\qquad n=\gamma\qquad PV^{\gamma}=C\quad\): 断熱変化
\(\qquad n=\infty\quad\,\, V=C\qquad\): 等積変化

【1】気体の比熱

熱力学の第1法則は
\(\,U\,\)を内部エネルギー、\(\,Q\,\)を熱量、\(\,W\,\)を仕事とすると
\(\quad dU=d’W+d’Q\quad \cdots\)(1)
と表せる。ここで \( d’\,\)は準静的過程を表す。
\(\quad d’W=-PdV\quad \cdots\)(2)
\(\quad dU=-PdV+d’Q\quad \cdots\)(3)
体積が一定として、\(dT\,\)で割ると
\(\quad C_V=\dfrac{d’Q}{dT}=\left(\dfrac{\partial U}{\partial T}\right)_V\quad \cdots\)(4)
同様に、圧力が一定とすれば
\(\quad C_P=\left(\dfrac{\partial U}{\partial T}\right)_P+P\left(\dfrac{\partial V}{\partial T}\right)_P\quad \cdots\)(5)

また、(4)式を \(T\)で積分すると\(\,\,U=C_VT\quad \cdots\)(6)
1モルでは \(\,\,PV=\mathrm{R}T\quad \cdots\)(7)\(\,\,\)で
\(\quad P\left(\dfrac{\partial V}{\partial T}\right)_P=\mathrm{R}\quad \cdots\)(8)　なので、(5)式は
\(\quad C_P=C_V+\mathrm{R}\quad \cdots \)(9)

【2】断熱変化

\(dU\,\)の微分を考える
\(\quad dU=\left(\dfrac{\partial U}{\partial T}\right)_VdT+\left(\dfrac{\partial U}{\partial V}\right)_TdV\quad \cdots\)(10)
これを(3)式に代入すると
\(\quad d’Q=\left(\dfrac{\partial U}{\partial T}\right)_VdT+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]dV\quad \cdots\)(11)
\(P=\)一定として(11)式を\(dT\,\)で割ると
\(\quad C_P=C_V+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]\left(\dfrac{\partial V}{\partial T}\right)_P\quad \cdots\)(12)
断熱変化では \(d’Q=0\,\)なので(11)式は
\(\quad \left(\dfrac{\partial U}{\partial T}\right)_VdT+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]dV=0\quad \cdots\)(13)
理想気体では\(\,(U\,\)は温度だけの関数なので \(\left(\dfrac{\partial U}{\partial V}\right)_T=0\)
(13)式に(6)式と(7)式を代入すると
\(\quad C_VdT+\dfrac{\mathrm{R}T}{V}dV=0\quad \cdots\)(14)
比熱比を\(\,\gamma=\dfrac{C_P}{C_V}\quad \cdots\)(15)\(\quad\)として(14)式を\(C_VT\,\)で割ると
\(\quad \dfrac{dT}{T}+(\gamma-1)\dfrac{dV}{V}=0\quad \cdots\)(16)\(\quad\)なので
\(\quad \ln T+(\gamma-1)\ln V= \text{一定} \cdots\)(17)\(\quad\)よって
\(\quad TV^{\gamma-1}= \text{一定} \cdots\)(18)
式(7)より\(\quad T=\dfrac{PV}{\mathrm{R}}\quad\cdots\)(19)を代入すると
\(\quad PV^{\gamma}=\text{一定}\quad \cdots\)(20)「ポアソンの法則」が得られる。
常温での\(\,C_V\,\)は並進運動と回転運動の自由度の\(\frac{\mathrm{R}}{2}\,\)倍となる。
単原子分子では並進運動の自由度が３なので、\(\,C_V=\frac{3}{2}\mathrm{R}\)。
２原子分子では\(\theta\,,\,\phi\,\)の回転が加わり、自由度が５になるので、\(\,C_V=\frac{5}{2}\mathrm{R}\)となる。
３原子分子(直線形)では、並進の自由度と回転の自由度は、２原子分子と同様だが振動の自由度が4となる。この振動は常温での比熱に寄与しないので、\(\,C_V\,\)は同じとなる。
よって、単原子分子は \(\gamma=\frac{5}{3}\,\)となり、２原子分子と直線形の３原子分子は \(\,\gamma=\frac{7}{5}\,\)となる。

［１］楕円の周の長さを求める

まず \(\,x=a\sin\theta\,,\,y=b\cos\theta\,\) で表される楕円の周の長さを求める．計算は第１象限の弧だけ求めて4倍することとする。

曲線の微少長さ\(\,ds\,\)はピタゴラスの定理から以下のようになる。

\(\quad ds=\sqrt{dy^2+dx^2}\quad\cdots\,\) (1)

弧の長さ(\(L\))は、これを全体に渡って積分することで求めることが出来る。

\(\quad x=a\sin\theta\,\) から\(\quad dx=a\cos\theta\,d\theta\,\)
\(\quad y=b\cos\theta\,\) から\(\quad dy=-b\sin\theta\,d\theta\,\)なので

\(\quad L=\displaystyle\int\sqrt{dy^2+dx^2}\,\)

\(\qquad =4\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{b^2\sin^2\theta+a^2\cos^2\theta}\,d\theta\)

\(\qquad =4a\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{1-\sin^2\theta+\frac{b^2}{a^2}\sin^2\theta}\,d\theta\)

ここで\(\,a\gt b\,\)として、\(\,q=\dfrac{a^2-b^2}{a^2}\,\)とおくと

\(\quad L=4a\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{1-q\sin^2\theta}\,d\theta\,\)となる

［２］級数展開

\(\sqrt{1-q\sin^2\theta}\,\)はそのままでは積分できないので、級数展開する。

例えば、\(\,(1+x)^m\,\)をマクローリン展開すると

\(\quad(1+x)^m=1+m\dfrac{x}{1!}+m(m-1)\dfrac{x^2}{2!}+\,m(m-1)(m-2)\dfrac{x^3}{3!}\)

\(\qquad \cdots+m\cdots(m-n+1)\dfrac{x^n}{n!}+\)

ここで、例えば　\(m=-\dfrac{1}{2}\)を代入すると

\(\quad(1+x)^{-\frac{1}{2}}=1+\left(-\dfrac{1}{2}\right)x+\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)\dfrac{x^2}{2!}\)

\(\qquad+\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)\left(-\dfrac{5}{2}\right)\dfrac{x^3}{3!}+\cdots\)

\(\qquad =1-\dfrac{1}{2}\dfrac{x}{1!}+\dfrac{1\cdot 3}{2^2}\dfrac{x^2}{2!}-\dfrac{1\cdot 3\cdot 5}{2^3}\dfrac{x^3}{3!}+\)

◎ここでは、\((1-x)^m=1-m\dfrac{x}{1!}+m(m-1)\dfrac{x^2}{2!}-\)で

\(\quad m=\dfrac{1}{2}\,\qquad x=q\sin^2\theta\,\)とすると

\((1-q\sin^2\theta)^{\frac{1}{2}}=1-\dfrac{1}{2}q\sin\theta-\dfrac{1}{2^2\cdot 2!}q^2\sin^4\theta\)

\(\qquad-\dfrac{1\cdot 3}{2^3\cdot 3!}q^3\sin^6\theta\cdots-\dfrac{1\cdot 3\cdot 5\cdot(2n-3)}{2^n\cdot n!}q^n\sin^{2n}\theta\,\cdots\)

［３］二重階乗

二重階乗\(\,n!!\,\)は自然数\(\,n\,\)に対して一つ飛ばしに積を取る。

\(\quad(2n)!!=(2n)(2n-2)(2n-4)\cdots(4)(2)=2^nn!\)

\(\quad(2n+1)!!=(2n+1)(2n-1)\cdots(3)(1)=\dfrac{(2n+1)!}{(2n)!!}\,\)

なので、一般項の分母 \(\,2^nn!\,\)は\(\,(2n)!!\,\)となる。

分子は\(\quad 1\cdot 3\cdot 5\cdot(2n-3)=\dfrac{(2n-1)!!}{2n-1}\,\) と表せる

［４］\(\,\sin^n\theta\,\)の積分

[2]で出てきた\(\,\,\displaystyle\int_0^{\frac{\pi}{2}}\sin^{2n}\theta\,\,\)はそのままでは計算できない。

まず、部分積分を再確認。

\(\,\,\displaystyle\int f(x)g'(x)dx=f(x)g(x)-\displaystyle\int f'(x)g(x)dx\,\)である。

\(\,I_n=\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx\,\,\)とすると、
\( I_0=\dfrac{\pi}{2}\,,\quad I_1=\left[-\cos x\right]_0^{\frac{\pi}{2}}=1\,\)となる

\(\,I_n=\displaystyle\int_0^{\frac{\pi}{2}}\sin^{n-1}x\sin x\,dx\,\)で

\(\,f(x)=\sin^{n-1}x\quad g(x)=-\cos x\,\)とおくと部分積分より

\(I_n=\left[-\sin^{n-1}x\cos x\right]_0^{\frac{\pi}{2}}+(n-1)\displaystyle\int_0^{\frac{\pi}{2}}\sin^{n-2}x\cos^2x\,dx\)

\(\,\,=0+(n-1)\displaystyle\int_0^{\frac{\pi}{2}}\sin^{n-2}x(1-\sin^2x)dx\)

\(\,\,=(n-1)\displaystyle\int_0^{\frac{\pi}{2}}\sin^{n-2}x\,dx-(n-1)\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx\)

\(n\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx=(n-1)\displaystyle\int_0^{\frac{\pi}{2}}\sin^{n-2}x\,dx\,\)なので

\(\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx=\dfrac{n-1}{n}\displaystyle\int_0^{\frac{\pi}{2}}\sin^{n-2}x\,dx\quad\)となるので

\(I_n=\dfrac{n-1}{n}I_{n-2}\quad\)という漸化式が求められる。より

\(I_n=\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx=\dfrac{(n-1))(n-3)\cdots}{n(n-2)(n-4)\cdots}\,\)

となり、(n,)が奇数の場合は

\(I_n=\dfrac{(n-1)(n-3)\cdots 4\cdot 2}{n(n-2)\cdots 5\cdot 3}I_1\,\)となり偶数では

\(I_n=\dfrac{(n-1)(n-3)\cdots 3\cdot 1}{n(n-2)\cdots 4\cdot 2}I_0\,\)となる。よって

\(\displaystyle\int_0^{\frac{\pi}{2}}\sin^{2n}\theta\,d\theta=\dfrac{(2n-1)!!}{(2n)!!}\dfrac{\pi}{2}\,\)となる。

[５］弧の長さの計算

これで、準備が終わったので \(\,L\,\)の長さを計算する。

\(L=4a\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{1-q\sin^2\theta}\,d\theta\qquad q=(a^2-b^2)/a^2\)

\(\quad=4a\displaystyle\int_0^{\frac{\pi}{2}}\left(1-\displaystyle\sum_{n=1}^{\infty}\dfrac{(2n-1)!!}{(2n)!!}\dfrac{q^n}{2n-1}\sin^{2n}\theta\right)d\theta\)

\(\,=4a\displaystyle\int_0^{\frac{\pi}{2}}d\theta-\displaystyle\sum_{n=1}^{\infty}\dfrac{(2n-1)!!}{(2n)!!}\dfrac{q^n}{2n-1}4a\displaystyle\int_0^{\frac{\pi}{2}}\sin^{2n}\theta\,d\theta\)

\(\,=2a\pi\left(1-\displaystyle\sum_{n=1}^{\infty}\left[\dfrac{(2n-1)!!}{(2n)!!}\right]^2\dfrac{q^n}{2n-1}\right)\)

これで、計算完了。結構面倒くさい！！

［６］楕円積分

楕円の弧の長さの計算に使った積分は「第2標準形の完全楕円積分」というらしい。

\(E(m)=\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{1-m\sin^2\theta}\,d\theta=\dfrac{\pi}{2}\left(1-\displaystyle\sum_{n=1}^{\infty}\left[\dfrac{(2n-1)!!}{(2n)!!}\right]^2\dfrac{m^n}{2n-1}\right)\)

振り子の計算で使った「第1標準形の完全楕円積分」は\(\,K(m)\,\)の形で表される積分で

\(K(m)=\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{d\theta}{\sqrt{1-m\sin^2\theta}}\quad\)の様に書かれます。

楕円の弧の計算と同様に級数展開します。

\((1-m\sin^2\theta)^{-\frac{1}{2}}=1+\dfrac{1}{2}m\sin^2\theta+\dfrac{3}{8}m^2\sin^4\theta\)

\(\qquad+\dfrac{15}{48}m^3\sin^6\theta+\cdots=\displaystyle\sum_{n=1}^{\infty}\dfrac{(2n-1)!!}{(2n)!!}m^n\sin^{2n}\theta\)

この級数も \(\,m\lt 1\,\)の範囲で一様収束するので、項別積分が可能です。

\(\displaystyle\int_0^{\frac{\pi}{2}}((1-m\sin^2\theta)^{-\frac{1}{2}}d\theta=\displaystyle\int_0^{\frac{\pi}{2}}\displaystyle\sum_{n=1}^{\infty}\dfrac{(2n-1)!!}{(2n)!!}m^n\sin^{2n}\theta\)

\(\qquad=\displaystyle\sum_{n=1}^{\infty}\dfrac{(2n-1)!!}{(2n)!!}m^n\displaystyle\int_0^{\frac{\pi}{2}}\sin^{2n}\theta\,d\theta\)

\(\qquad=\dfrac{\pi}{2}\left(\displaystyle\sum_{n=1}^{\infty}\left[\dfrac{(2n-1)!!}{(2n)!!}\right]^2\,m^n\right)\)

エネルギー保存の法則から振り子の周期 \(T\) の式を求める。
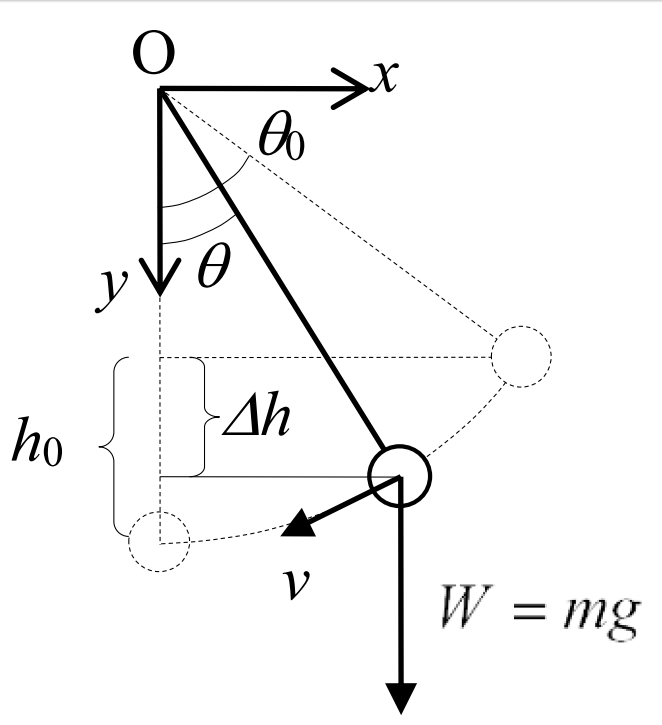振り子の支点より水平方向に \(\ x\ \)軸をとり、鉛直方向に \(\ y\ \)軸をとると、エネルギー保存則から、次式が成立する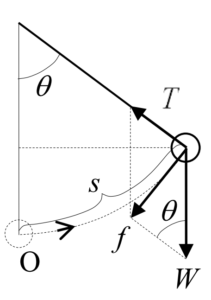

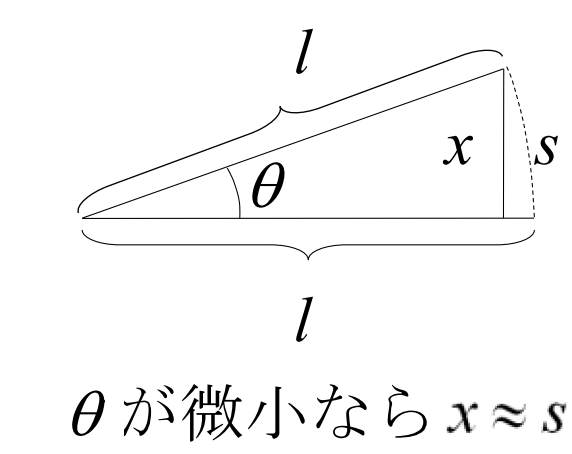\( \dfrac{1}{2}mv^2=mg\Delta h\quad\) (21)

ここで、\(\ v\ \)は重りが円周方向に移動する速度で、\(\Delta h\ \)は重りの落下距離である。ここで

\(\Delta h=l\cos\theta-l\cos\theta_0=l\ (\cos\theta-\cos\theta_0)\quad\) (22)
なので

\( \dfrac{1}{2}mv^2=mgl(\cos\theta-\cos\theta_0)\)
\( \therefore \ v=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\) (23)

さらに

\( v=\dfrac{ds}{dt}=l\dfrac{d\theta}{dt}\quad\) (24)

なので、以下の式が得られる。

\( l\dfrac{d\theta}{dt}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\quad\)(25)

\( dt=\dfrac{1}{\sqrt{2}\omega}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (26)

\(\quad\because\,\,\omega:=\sqrt{\dfrac{g}{l}}\)

この(26)式を積分すると周期を求めることが出来る。積分範囲を4分の1周に相当する \(\ t=T/4\ \)とすると、右辺の積分範囲は\(\ \theta=0\sim\theta_0\ \)となるので、

\( \displaystyle\int_0^{\frac{T}{4}}dt=\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (27)

\(\therefore\,\, T=4\dfrac{1}{\sqrt{2}\omega}\displaystyle\int_0^{\theta_0}\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}\quad\) (28)

この積分を行うために、半角公式を使って以下の変換を行う

\( \cos\theta=1-2\sin^2\frac{\theta}{2}\quad\cos\theta_0=1-2\sin^2\frac{\theta_0}{2}\)

ここで \(\,\,k:=\sin\frac{\theta_0}{2}\quad \sin\phi:=\sin\frac{\theta}{2}/k\,\,\)とすると

\( \cos\theta-\cos\theta_0=1-2\sin^2\frac{\theta}{2}-\left(1-2\sin^2\frac{\theta_0}{2}\right)\)

\(\quad=2\left(\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}\right)=2k^2\cos^2\phi\,\,\)となる

\(k\sin\phi=\sin\frac{\theta}{2}\,\,\)を両辺微分して\(\,\,k\cos\phi\,d\phi=\frac{1}{2}\cos\frac{\theta}{2}\,d\theta\)

\(d\theta=\dfrac{2k\cos\phi\,d\phi}{\cos\frac{\theta}{2}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-\sin^2\frac{\theta}{2}}}=\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\)

なので

\(\dfrac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}=\dfrac{1}{\sqrt{2}k\cos\phi}\dfrac{2k\cos\phi\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\)

\(\quad=\dfrac{\sqrt{2}\,d\phi}{\sqrt{1-k^2\sin^2\phi}}\,\,\)となり、第１種楕円積分の形になる。

［１］運動方程式

振り子には、図のような力が働く。ここで 重力は\( \ W=mg\ \)で糸の張力は\(\ \ T=W\cos\theta\ \) である。

\(W\ \)と\(\ T\ \)の合力\(\ f\ \)の向きは図のように半径\(\ l\ \)の円周の接線方向となり、その大きさは

\(f=W\sin\theta=mg\sin\theta\)　(1)

である。この合力\(\ f\ \)により、重りは円弧を描くように往復運動をする。ここで、運動を円軌道として考えるために、振り子の釣り合いの位置 O から、円弧に沿って\(\ s\ \)軸をとる。この合力\(\ f\ \)は重りを\(\ s\ \)軸の負の方向に運動させる力となるため、重りの運動方程式は

\( m\dfrac{d^2s}{dt^2}=-f=-mg\sin\theta\ \)　(2)

すなわち

\( \dfrac{d^2s}{dt^2}=-g\sin\theta\ \)　(3)

と表すことが出来る。　円弧の長さは \(\ s=l\ \theta\ \)で表せられ、２回微分は

\(\ \dfrac{d^2s}{dt^2}=l\dfrac{d^2\theta}{dt^2}\ \)　(4)

となるので、運動方程式は重りの角度\(\ \theta\ \)に対して

\( \dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\sin\theta\ \)　(5)

と表すことが出来る。

［２］運動方程式の近似解

　(5)式の運動方程式は、三角関数を含んでいるため、このままでは階を求めることが難しい。但し、円弧の角度\(\ \theta\ \)が微少の場合、三角形の高さ\(\ x=\sin\theta\ \)は円弧の長さ\(\ s\ \)にほぼ等しくなり
\(\quad x\ \approx\ s\ \)とおけるため

\( \sin\theta=\dfrac{x}{l}\ \approx\ \dfrac{s}{l}=\dfrac{l\theta}{l}=\theta\ \)　(6)

となり、運動方程式は

\( \dfrac{d^2\theta}{dt^2}=-\omega^2\theta\qquad \omega:=\sqrt{\dfrac{g}{l}}\quad\) (7)

と表すことが出来る。これは単振動で良く近似出来る。一般解は

\( \theta=A\sin\omega t+B\cos\omega t \)　(8)

ここで、 \( t=0\ \)で\(\ \theta=\theta_0\ \)として、(8)式に代入すると

\( \theta_0=A\sin\omega\times 0+B\cos\omega\times 0=B\quad\therefore B=\theta_0\)

つぎに、(8)式を \(t\) で微分して、\(\ t=0\ \)で\(\ \dfrac{d\theta}{dt}=0\ \) とすると

\( \dfrac{d\theta}{dt}=A\omega\cos\omega t-B\omega\sin\omega t\)

\(\qquad =A\omega\cos\omega\times 0-B\omega\sin\omega\times 0=A\omega=0 \)

よって、\(\ A=0\ \)となり、(8)式は\(\quad\theta=\theta_0\cos\omega t\ \) (9)

と決定される。このように解が周期関数で表される振動を単振動といい、単振動で近似出来る振り子を単振り子といいます。

\(\ \omega=\sqrt{\cfrac{g}{l}}\ \) は角振動数 [rad/s] と呼ばれる。

角振動数\(\ \omega\ \)を 2\(\pi\) で割った値は、重りが1秒間に往復する回数を表し、振動数 \(\ f\ \)[Hz}と呼ばれています。

\( f=\dfrac{\omega}{2\pi}=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}\ \,\,\) Hz\(\quad\)(10)

重りが一往復するのに必要な時間は、周期 \(T\) [s] といい、振動数の逆数になる。

\(T=\dfrac{1}{f}=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{l}{g}}\quad\)(11)

TeX test

$$ x^2=c$$
$$\nabla=\dfrac{\partial}{\partial x} $$