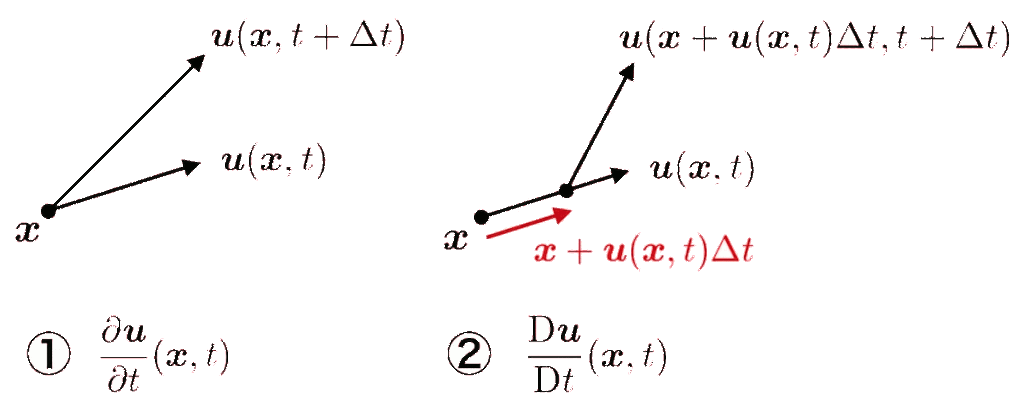\(\def\bm{\boldsymbol}\)\(\def\di{\displaystyle}\)\(\def\ve{\varepsilon_0}\)\(\def\dd#1#2{\dfrac{\partial #1}{\partial #2}}\)\(\def\dda#1#2{\dfrac{\partial^2 #1}{\partial #2}}\)
1. 流体粒子と流体運動の扱い
流体を考える際、2つの捉え方がある。
[1] ラグランジュの方法( Lagrange )
物体(固体)の運動と同様、各流体粒子に着目して、各流体粒子が時間の経過とともに、どのように動くかを追跡していく方法である。
この方法は、一つの流体粒子の経路や加速度を知る上では便利ではあるが、流れ場が全体的にどのようになっているかを知るには適さない。
[2] オイラーの方法( Euler )
この方法は、特定の流体粒子を追跡するのではなく、流れ場全体の様子をそれぞれの時刻に一度に調べる方法である。すなわち、流速や圧力を、座標\(\,\,x\,,\,y\,,\,z\,,\,\)および時間\(\,t\,\)の関数として表す。この方法は、流体の運動を調べる流体力学において、一般に用いられる方法である。
2. テーラー展開
まずは、数学の準備をします。
[1] 1 変数でのテーラー展開
\(\quad\)関数\(\,f(x)\,\)において、点\(\,a\,\)の周りでテーラー展開すると
\begin{equation}f(x)=f(a)+f^{\prime}(a)(x-a)+\dots+\dfrac{f^{(n)}(a)}{n!}(x-a)^n+\cdots
\end{equation}\(\quad\)ここで、\(\,x\,\to\,x+\Delta x\,\quad a\,\to\,x\,\) と置き換えると
\begin{equation}
f(x+\Delta x)=f(x)+(\Delta x)\,f^{\prime}(x)+\dfrac{(\Delta x)^2}{2!}f^{\prime\prime}(x)+\cdots+\dfrac{(\Delta x)^n}{n!}f^{(n)}(x)+\cdots
\end{equation}[2] 多変数のテーラー展開\begin{align}f(x+\Delta x,& y+\Delta y,z+\Delta z)=f(x,y,z)+\left(\Delta x \dd{}{x}+\Delta y\dd{}{y}+\Delta z\dd{}{z}\right)f(x,y,z)\\ &+\dfrac{1}{2!}\left(\Delta x \dd{}{x}+\Delta y\dd{}{y}+\Delta z\dd{}{z}\right)^2f(x,y,z)+\cdots \end{align}\(\quad\)ここで、\(\bm{x}=^t(\,x,\,y,\,z)\,\,\,\,\bm{h}=^t(\Delta x,\Delta y,\Delta z)\,\)とおくと、\begin{equation} f(\bm{x}+\bm{h})=f(\bm{x})+\sum_{n=0}^{\infty}\dfrac{1}{n!}(\nabla\cdot\bm{h})^nf(\bm{x})\qquad\text{と表すことができる}\end{equation}
3. ラグランジュ微分
ラグランジュ微分とは、オイラーの方法とラグランジュの方法の両方の流儀を混ぜ合わせたような概念である。時々刻々と移動していく流体の「ある一部分」を追いかけながら、その「一部分」が持つ物理量\(\,A\,\)の時間的な変化を考える。
時刻\(\,t\,\)に、位置\(\,\bm{x}=(x,y,z)\,\)にある速度\(\,\bm{u}=(u_x,u_y,u_z)\,\)の流体の持つ物理量を\(\,A(x,y,z,t)\,\)と表す。\(\,\Delta t\,\)秒後にはこの流体はおよそ\(\,(\,x+u_x\Delta t,\,y+u_y\Delta t,\,z+u_z\Delta t\,)\,\)付近に移動していることであろう。つまり、\(\,\Delta t\,\)秒後がの移動後の地点での物理量は\(\,A(x+u_x\Delta t,y+u_y\Delta t,z+u_z\Delta t,t+\Delta t)\,\)となる。
これをテーラー展開の一次で近似すると\begin{align}A(x+u_x\Delta t,& y+u_y\Delta t,z+u_z\Delta t,t+\Delta t)\\&\doteq A(x,y,z,t)+\dd{A}{x}u_x\Delta t+\dd{A}{y}u_y\Delta t+\dd{A}{z}\Delta t+\dd{A}{t}\Delta t\end{align}変化分を計算すると\begin{align}\Delta A&\doteq A(x+u_x\Delta t,y+u_y\Delta t,z+u_z\Delta t,t+\Delta t)-A(x,y,z,t)\\&\doteq\dd{A}{x}u_x\Delta t+\dd{A}{y}u_y\Delta t+\dd{A}{z}u_z\Delta t+\dd{A}{t}\Delta t\\&=\left(\dd{A}{x}u_x+\dd{A}{y}u_y+\dd{A}{z}u_z+\dd{A}{t}\right)\Delta t\qquad\cdots\quad\text{(1)}\end{align}これを時間経過による変化割合で表すと\begin{equation}\dfrac{\Delta A}{\Delta t}\doteq\dd{A}{x}u_x+\dd{A}{y}u_y+\dd{A}{z}u_z+\dd{A}{t}\qquad\cdots\quad\text{(2)}\end{equation}(1)式の近似には\(\,\Delta t\,\)の2乗以上に比例する程度の誤差があり、それを\(\,\Delta t\,\)で割った(2)式には\(\,\Delta t\,\)あるいは\(\,\Delta t\,\)の2乗以上に比例するような誤差が含まれているが、ここで\(\,\Delta t\,\to\,0\,\)の極限を考えれば無視できるようになるので、それを等式を使って次のように表す。\begin{equation}\dfrac{DA}{Dt}=\dd{A}{x}u_x+\dd{A}{y}u_y+\dd{A}{z}u_z+\dd{A}{t}\qquad\cdots\quad\text{(3)}\end{equation}これが、「ラグランジュ微分」「物質微分」などと呼ばれているものである。これは、流体と一緒に流れている人から見た、その地点での物理量\(\,A\,\)の時間的な変化率である。
物理量\(\,A\,\)を省いて、順序を変えると以下のようになる。
\begin{equation}\dfrac{D}{Dt}\equiv u_x\dd{}{x}+u_y\dd{}{y}+u_z\dd{}{z}+\dd{}{t}=\bm{u}\cdot\nabla+\dd{}{t}\quad\cdots\quad\text{(4)}\end{equation}流体の加速度をその点での微分とラグランジュ微分で比べたのが、下の図である。