放送大学のオンライン授業で「力学演習」を履修している。そこでの練習問題で一次元の弾性衝突問題があり、すっかり忘れているので再確認のため、計算してみました。
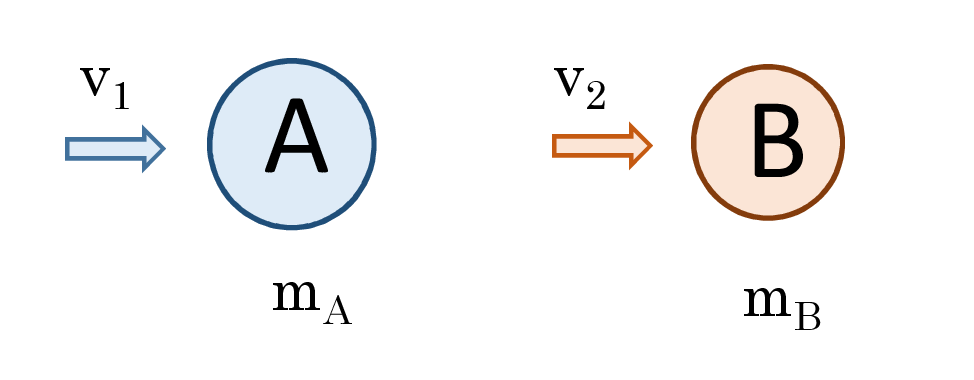
図のような2球で考える。向きは\(\,x\,\)軸方向に正として、初速度をそれぞれ\(\,v_1\,\,,\,v_2\,\)とする。衝突後の速度をそれぞれ\(\,v_3\,\,,\,v_4\,\)とする。弾性衝突なので、運動量とエネルギーが保存する。
・運動量保存
\(\qquad m_A\,v_1+m_B\,v_2=m_A\,v_3+m_B\,v_4\quad\cdots\,\)(1)
・エネルギー保存
\(\qquad \dfrac{1}{2}m_A\,v_1^2+\dfrac{1}{2}m_B\,v_2^2=\dfrac{1}{2}m_A\,v_3^2+\dfrac{1}{2}m_B\,v_4^2\quad\cdots\,\)(2)
式(1)から、\(\quad v_4=\dfrac{m_A(v_1-v_3)+m_Bv_2}{m_B}\quad\cdots\,\)(3)
式(2)から、\(\quad v_4^2=\dfrac{m_A(v_1^2-v_3^2)+m_Bv_2^2}{m_B}\quad\cdots\,\)(4)
式(3)を2乗すると、
\(\quad v_4^2=\dfrac{m_A^2v_1^2-2m_A^2v_1v_3+m_A^2v_3^2+m_B^2v_2^2+2m_Am_Bv_1v_2-2m_Am_Bv_2v_3}{m_B^2}\quad\cdots\,\)(5)
式 (4)\(\,=\,\)(5) なので、
\(\quad m_Am_Bv_1^2-m_Am_Bv_3^2+m_B^2v_2^2\)
\(\qquad\qquad =m_A^2v_1^2-2m_A^2v_1v_3+m_A^2v_3^2+m_B^2v_2^2+2m_Am_Bv_1v_2-2m_Am_Bv_2v_3\quad\cdots\,\)(6)
\(\quad m_A^2v_1^2-2m_Av_1v_3+m_A^2v_3^2+2m_Am_Bv_1v_2-2m_Am_Bv_2v_3-m_Am_Bv_1^2+m_Am_Bv_3^2=0\,\cdots\,\)(7)
\(\quad(m_A+m_B)v_3^2-2(m_Av_1+m_Bv_2)v_3+m_Av_1^2+2m_Bv_1v_2-m_Bv_1^2=0\quad\cdots\,\)(8)
この式(8) を\(\,v_3\,\)の2次方程式として解くと
\(\quad v_3=\dfrac{m_Av_1+m_Bv_2\pm\sqrt{m_B^2(v_1-v_2)^2}}{m_A+m_B}=\dfrac{m_Av1+m_Bv_2\pm m_B|v_1-v_2|}{m_A+m_B}\quad\cdots\,\)(9)
ここで、球 A の速度が B の速度より大きいケースで考えてみる。 \(\,v_1\ge v_2\)
\(\,\pm\,\)の\(\,+\,\)では、\(\,v_3=v_1\,\)となり、すり抜ける形なので\(\,-\,\)を採用する。
\(\quad v_3=\dfrac{m_Av_1-m_Bv_1+2m_Bv_2}{m_A+m_B}\quad\cdots\,\)(10)
ここで、両方の球の質量が同じ場合、\(\,v_3=v_2\,\)となり、A と B の運動量が入れ替わることになる。
◇ 大小球の正面衝突
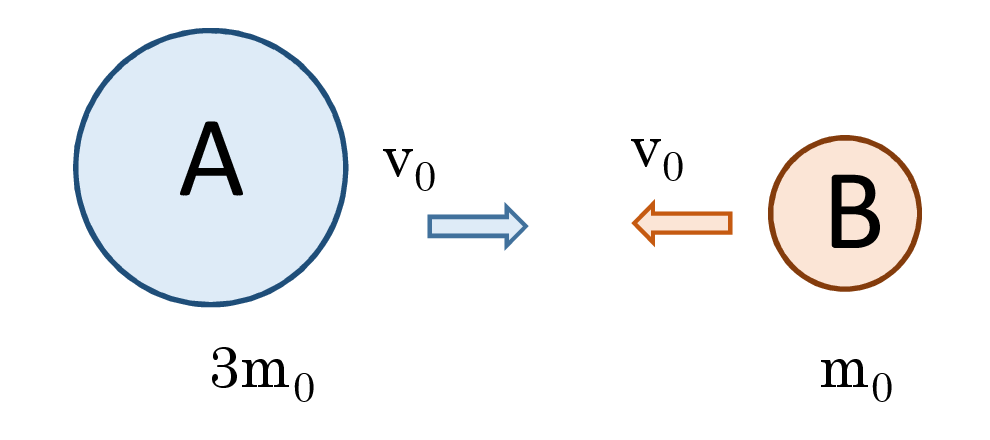
大小の球を正面衝突させた場合を考える。
Aは\(\,m_A=3m\,\)とし、Bは\(\,m_B=m\,\)とする。
速度はともに\(\,v_1=v_2=v_0\,\)(符号は正負となる)として、正面からの衝突とする。
式(10)と式(1)により
\(\quad v_3=\dfrac{3mv_0-mv_0-2mv_0}{3m+m}=0\quad v_4=\dfrac{3mv_0-mv_0}{m}=2v_0\,\)となる。
結局、Aは停止しBは速度\(\,2v_0\,\)で反対側に跳ね返ることになる。
◇ 3球での衝突問題
『中川のビジュアル物理学教室』のページの中の「解説:一次元衝突」に次のような3球の衝突が紹介されていました。(画像は中川氏のページのものを使わせてもらいました)
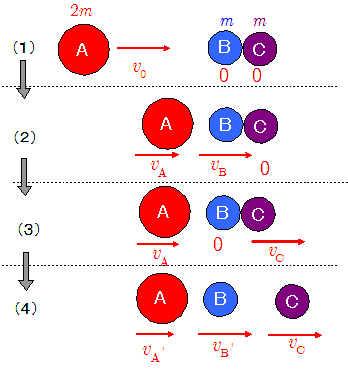
静止している球B,Cに,その2倍の質量をもつ球Aを\(\,v_0\,\)で弾性衝突したらどうなるだろうか?
この問題は,過去に青学大の入試問題として出題されたことがあるという事でした。
まず、Aが静止しているBに衝突する時点を考える。式(10) に\(\,m_A=2m\,,\,m_B=m\,,\,v_1=v_0\,,\,v_2=0\,\)を代入すると、
\(\quad v_A=v_3=\dfrac{2mv_0-mv_0}{3m}=\dfrac{1}{3}v_0\quad\cdots\,\)(11)
静止していたBの速さ\(\,v_B\,\)は、式(11)の値を式(1)に代入すると\(\,v_B=v_4=\dfrac{4}{3}v_0\,\)となる。
Bがこの速度\(\,v_B\,\)で、静止しているCに衝突すると
BとCは同質量なので、式(11)より、Bは停止してCは速度\(\,v_C=v_B\,\)で動き出すことになる。
停止した(1回動いて停止した形になる)BにAが\(\,v_A=\dfrac{1}{3}v_0\,\)で衝突することになる。
同じく、式(11)に代入すると、再度のAの速度\(\,v_A’\,\)は
\(\quad v_A’=\dfrac{2m\frac{1}{3}v_0-m\frac{1}{3}v_0}{3m}=\dfrac{1}{9}v_0\quad\cdots\,\)(12)
これを式(1)に代入すると\(\quad2m\dfrac{1}{3}=2m\dfrac{1}{9}v_0+mv_B’\,\)より
Aは\(\,\dfrac{1}{9}v_0\,\)で動き出し、Bは\(\,\dfrac{4}{9}v_0\,\)で動き出す。
Cは先程、Bの衝突で\(\dfrac{4}{3}v_0\,\)で動き出しているので、3球はバラバラになることになる。