1. ミクロの世界の量子状態
1-1. 箱の中の粒子
一次元の粒子の波動方程式を考える。\(\,x\,\)軸上に、\(\,x=0\,\)から\(\,x=L\,\)までの長さが\(\,L\,\)の区間(\(\,0\ge\,x\ge\,L\,\))を考え、この区間の内部でだけ粒子が運動できるモノとする。このような状況の粒子を、1次元の箱の中の粒子と呼ぶ。
箱の外に出られないように、箱の外の位置エネルギーを\(\,\infty\,\)とする。また、箱の中では粒子に力が働かず自由に運動できるように、位置エネルギーを\(\,0\,\)とする。
解くべき方程式は、定常状態の波動方程式 \(\,\hat{H}\phi(x)=E\phi(x)\,\) であり、粒子の質量を\(\,m\,\)とするとハミルトニアン\(\,\hat{H}\,\)は以下のようになる。
\(\quad \hat{H}=-\dfrac{\hbar^2}{2m}\Delta+U(x)\quad\cdots\,\)(1.1)
変数は\(\,x\,\)のみの1次式なので、ラプラシアン\(\,\Delta\,\)は\(\,x\,\)の2次微分 \(\,d^2/dx^2\,\)に等しい。箱の外では位置エネルギーが無限大だから、\(\,\hat{H}\phi=E\phi\,\)が成り立つためには、\(\phi=0\,\)にならなければならない。
すなわち、箱の外の確率密度は\(\,0\,\)になり、粒子は箱の外には存在しない。次に箱の中では、位置エネルギーを\(\,U(x)=0\,\)としたので、波動方程式は次のような2次微分を含む方程式になる。
\(\quad -\dfrac{\hbar^2}{2m}\ \dfrac{d^2\phi}{dx^2}=E\phi\quad\cdots\,\)(1.2)
この式では\(\,\phi\,\)と\(\,x\,\)以外はすべて定数であり、次の形の基本的な微分方程式となっている
\(\quad \dfrac{d^2\phi}{dx^2}=-k^2\phi\quad\cdots\,\)(1.3)
ここで右辺の\(\,k\,\)は、求めるべきエネルギー\(\,E\,\)を含み、次式で与えられる定数である
\(\quad k=\left(\dfrac{2mE}{\hbar^2}\right)^{1/2}\quad\cdots\,\)(1.4)
式 (1.3)の一般解は指数関数または三角関数を含む次式の形に表される
\(\quad \phi(x)=ae^{ikx}+be^{-ikx}=A\sin kx+B\cos kx\quad\cdots\,\)(1.5)
波動関数の重要な性質として、連続性の条件があり、境界条件を考慮しなければならない。
箱の外では\(\,\phi=0\,\)であるから、箱の中(\(\,0\ge x\ge L\,)\)の\(\,\phi\,\)も箱の両端で値が\(\,0\,\)にならなくてはいけない。
そこで境界条件として \(\,\phi(0)=\phi(L)=0\,\) を使うと、\(\,x=0\,\)で\(\,\cos\,\)関数の部分は\(\,0\,\)にならないので、\(\sin\,\)の関数部分だけが残る。
また、\(\,x=L\,\)で\(\,\sin kx\,\)の値が\(\,0\,\)になるには \(\,kL=n\pi\,\)となり、その結果、波動関数とエネルギーがそれぞれ次のように決まる。
\(\quad\phi(x)=A\sin(n\pi x/L)\quad\cdots\,\)(1.6)
\(\quad E=\dfrac{(n\pi\hbar/L)^2}{2m}\quad\cdots\,\)(1.7)
ここで整数\(\,n\,\)は\(\,1,2,3\,\)などの自然数であり、これは量子数と呼ばれる。
(1.7) 式から、箱の中の粒子に許されるエネルギーは、図のように飛び飛びのエネルギー準位になる。
この結果は有限な空間に閉じ込められた粒子のエネルギーが飛び飛びになって量子化されることを示している。
ここで注目するべきことは、エネルギーが最低の基底状態、すなわち\(\,n=1\,\)の状態でも、エネルギーが\(\,0\,\)にならないことである。このエネルギーをゼロ点エネルギーという。
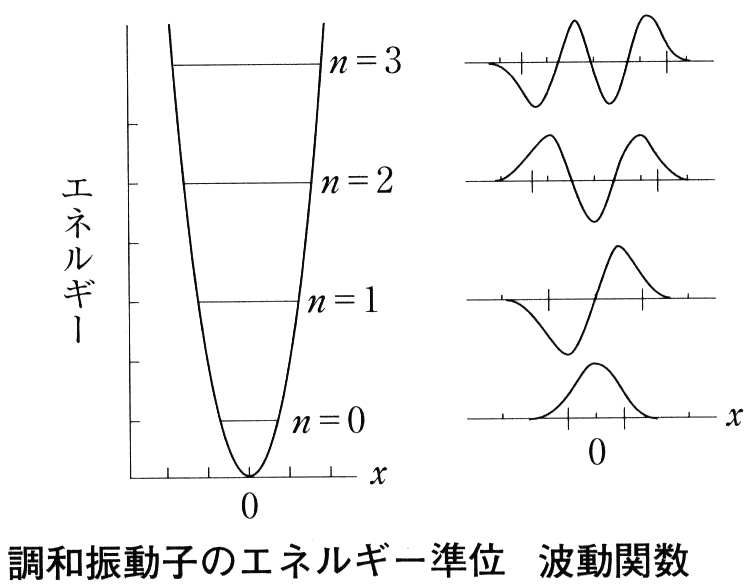 (1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。
(1.7) 式で与えられる波動関数は図の中央に示したように、エネルギー準位を区別する量子数\(\,n\,\)が増えるにつれ上下の振動が激しくなる。波動関数の値が\(\,0\,\)になる位置を節(ふし)という。
節になる位置は、\(\phi\,\)でも\(\,\phi^2\,\)も同じであり、図の右に示した\(\,\phi^2\,\)の図から明らかなように、節の位置に粒子が観測される確率は\(\,0\,\)である。
1-2. 調和振動子
 波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。
波動方程式の簡単な例として、左図のようなバネ(バネ定数を\(\,k\,\))につるされた質量\(\,m\,\)の錘(おもり)の振動を考える。位置エネルギーは、\(\,U(x)=\frac{1}{2}kx^2\,\) であり、釣り合った位置から\(\,x\,\)だけ錘がずれると、図の右に示した放物線に沿って上がって行き、常に中心に引き戻される力が働いて振動する。このような振動を調和振動子という。
この場合のハミルトニアンの運動エネルギーは箱の中の粒子の場合と同じになり、位置エネルギーは\(\,U(x)=\frac{1}{2}kx^2\,\) であるから、この調和振動子の波動方程式は次のように表される。
\(\left(-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2}+\dfrac{1}{2}kx^2\right)\Psi=E\Psi\quad\cdots\,\)(1.8)
この微分方程式は、次のように波動関数を仮定すると解くことができる。
\(\quad\Psi(x)=e^{-ax^2}\,\displaystyle\sum_{i=0}b_ix^i\quad\cdots\,\)(1.9)
解いた結果、次式に従うエネルギー準位が得られる。
\(\quad E_n=\left(n+\dfrac{1}{2}\right)h\nu\qquad(n=0,1,2,\cdots)\quad\cdots\,\)(1.10)
ここで、\(\,n=0,1,2,\cdots\,\) は振動の量子数(振動量子数)であり、\(h\,\)はプランク定数で、\(\nu\,\)はこの振動の固有振動数である。

調和振動子に許されるエネルギー準位は図の左に示すように等間隔になる。その間隔は、振動のエネルギー量子\(\,h\nu\,\)であり,固有振動数\(\,\nu\,\)はバネの力の定数が\(\,k\,\)で質量が\(\,m\,\)の古典力学の振動子と全く同じで、次式によって与えられる。
\(\quad\nu=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}\quad\cdots\,\)(1.11)
量子論の振動子には、古典力学と明らかに違った注目すべき特徴がある。エネルギーが最低の状態(基底状態)でも、そのエネルギーは\(\,0\,\)にならず、\(\,\dfrac{1}{2}h\nu\,\)というエネルギーをもって振動する。このエネルギーをゼロ点エネルギーといい、その時の振動をゼロ点振動という。
図の左に示したように、調和振動子の波動関数は中心の周りで振動子、遠くに行くと減衰する。値が\(\,0\,\)になる節の数は量子数\(\,n\,\)に等しく、エネルギーが高いほど多くなる。
1-3. 2粒子系の運動方程式
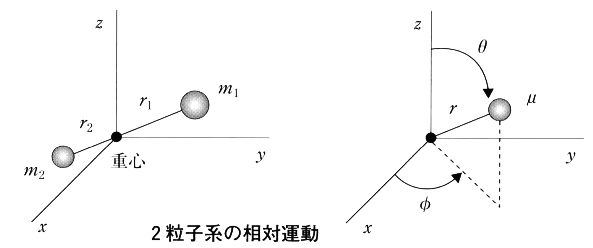 2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。
2個の粒子を含む場合すなわち2粒子系の波動方程式は、以下のように取り扱うと1個の粒子の問題になり簡単になる。図の左に示したように、質量\(\,m_1\,\)と\(\,m_2\,\)の2個の球が距離$r$で結ばれているとして、その運動を考える。
ここで重心を座標原点に固定すると、\(\,r_1\,\)と\(\,r_2\,\)の和が\(\,r\,\)になり、2個の粒子の相対運動は長さが\(\,r\,\)の棒の先端につけた1つの球の運動の問題に単純化される。そのとき先端の粒子の質量\(\,\mu\,\)は、2個の粒子の質量の逆数の和の逆数になる。
\(\quad\)換算質量\(\quad\mu=\dfrac{1}{\frac{1}{m_1}+\frac{1}{m_2}}\)
こうして2個の粒子の相対運動は、換算質量をもつ1つの粒子の運動として取り扱うことが出来る。したがって、その波動方程式は次のように、1つの粒子の方程式と同じになる。
\(\quad\left(-\dfrac{\hbar^2}{2\mu}\Delta+U\right)\Psi=E\Psi\quad\cdots\,\)(1.13)
このような問題では、原点からの距離\(\,r\,\)が特別に重要なので、直交座標系\(\,(x,y,z)\,\)の代わりに、図の右に示す3次元の極座標\(\,(r,\theta,\varphi\,)\,\)を変数にとる。すると体積要素\(\,dxdydz\,\)とラプラシアン\(\,\Delta\,\)は、以下のように表される。
\(\quad\)体積要素\(\quad dxdydz=r^2\sin\theta dr d\theta d\varphi\quad\cdots\,\)(1.14)
\(\quad\)ラプラシアン\(\quad \Delta=\dfrac{1}{r^2}\dfrac{\partial}{\partial r}\left(r^2\dfrac{\partial}{\partial r}\right)+\dfrac{1}{r^2}\Lambda\quad\cdots\,\)(1.15)
\(\quad\)ルジャンドリアン\(\quad \Lambda=\dfrac{1}{\sin\theta}\dfrac{\partial}{\partial\theta}\left(\sin\theta\dfrac{\partial}{\partial\theta}\right)+\dfrac{1}{\sin^2\theta}\dfrac{\partial^2}{\partial\varphi^2}\quad\)(1.16)
ここで、(1.15)式のラプラシアンに含まれる\(\,\Lambda\,\)は角度に依存する演算子であり、ルジャンドリアンと呼ばれる。
1-4. 剛体回転子
2量子系の波動方程式は、換算質量\(\,\mu\,\)を使うと原点から距離\(\,r\,\)のところに繋がれた1個の粒子の回転運動になる。距離\(\,r\,\)が一定なので\(\,r\,\)に関する微分は消えてしまい、また位置エネルギーも\(\,0\,\)とおいてよいので、その波動方程式は次のように単純な式になる。
\(\quad-\dfrac{\hbar^2}{2I}\Delta\Psi=E\Psi\quad\cdots\,\)(1.17)
ここで、次式で表される\(\,I\,\)は、重心を軸とする回転運動の慣性モーメントである。
\(\quad I=\mu r^2\quad\cdots\,\)(1.18)
(1.17)式の波動方程式は三角関数を組み合わせた式を仮定して解くことが出来、その結果、剛体回転子に許されるエネルギーは次式のように、整数値をとる回転量子数\(\,J\,\)によって飛び飛びの準位になる。
\(\quad E=\dfrac{J(J+1)\hbar^2}{2I}\qquad (J=0,1,2,\cdots)\quad\cdots\,\)(1.19)
剛体回転子の波動方程式は、数学でよく知られている球面調和関数\(\,Y_{J,m}(\theta,\varphi)\,\)というものになり、それは\(\,J\,\)のほかにもう一つの量子数\(\,m\,\)にも依存している。\(\,J\,\)が決まれば、それに従って\(\,m\,\)のとりうる範囲が決まる。\(\,m\,\)は\(\,J\,\)から\(\,J-1,J-2,\cdots,0,\cdots,-J\,\)まで、合計\(\,2J+1\,\)通りの値が可能である。
\(\quad Y_{00}(\theta,\varphi)=\left(\dfrac{1}{4\pi}\right)^{1/2}\quad\cdots\,\)(1.20)
\(\quad Y_{10}(\theta,\varphi)=\left(\dfrac{3}{4\pi}\right)^{1/2}\cos\theta\quad\cdots\,\)(1.21)
\(\quad Y_{1\pm1}(\theta,\varphi)=\mp\left(\dfrac{3}{8\pi}\right)^{1/2}\sin\theta\ e^{\pm i\varphi}\quad\cdots\,\)(1.22)
\(\quad Y_{20}(\theta,\varphi)=\left(\dfrac{5}{16\pi}\right)^{1/2}(3\cos^2\theta-1)(\quad\cdots\,\)(1.23)
\(\quad Y_{2\pm1}(\theta,\varphi)=\mp\left(\dfrac{15}{8\pi}\right)^{1/2}\sin\theta\ \cos\theta\ e^{\pm i\varphi}\quad\cdots\,\)(1.24)
\(\quad Y_{2\pm2}(\theta,\varphi)=\mp\left(\dfrac{15}{32\pi}\right)^{1/2}\sin^2\theta\ e^{\pm i2\varphi}\quad\)(1.25)
2.分子の回転
2-1. 回転運動のエネルギー
質量\(\,m\,\)、速度\(\,v\,\)の直線運動の大きさが運動量\(\,p=mv\,\)で、運動に伴うエネルギーは
\(\quad E=\dfrac{1}{2}mv^2=\dfrac{1}{2}\dfrac{p^2}{m}\quad\cdots\,\)(2.1)
である。一方、回転運動の大きさを表す量が角運動量であり、回転の軸から距離\(\,r\,\)にあって、運動量\(\,p\,\)で運動している物体の角運動量\(\,p_{\theta}\,\)は、
\(\quad p_{\theta}=r\times p\quad\cdots\,\)(2.2)
と表される。\(\,p_{\theta}\,\)は運動量を含むベクトルである。この角運動量を用いて、回転運動のエネルギーは
\(\quad E=\dfrac{1}{2}\dfrac{p_{\theta}^2}{I}\quad\cdots\,\)(2.3)
のように表される。式(2.1)と(2.3)を比較すると対応していることが分かる。
 直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは
直線運動を行う物体で運動の持続性(慣性)に影響する量である質量に対応するのが、回転運動における\(\,I\,\)であり、慣性モーメントと呼ばれる。慣性モーメントは
\(\quad I=\sum_im_ir_i^2=\sum_im_i(x_i^2+y_i^2+z_i^2)\quad\)(2.4)
であるが、2原子分子では換算質量\(\,\mu\,\)と原子間の距離\(\,r\,\)を使うと、以下の簡単な式で表すことが出来る
\(\quad \mu=\dfrac{m_1\cdot m_2}{m_1+m_2}\quad\cdots\,\)(2.5)
\(\quad I=\mu r^2\quad\cdots\,\)(2.6)
式(2.3)には運動量\(\,p_{\theta}\,\)が含まれており、この式を量子の世界にもちこむには、その\(\,p_{\theta}\,\)を演算子に置き換えればよい。その結果
\(\quad p_{\theta}=\sqrt{J(J+1)}\hbar\quad\cdots\,\)(2.7)
と置き換えることが出来る。従って、式(2.3)の2原子分子の場合の量子論的な表現は式(1.19)のように
\(\quad E=\dfrac{J(J+1)\hbar^2}{2I}=BJ(J+1)\qquad (J=0,1,2,\cdots)\quad\cdots\,\)(2.8)
となる。ここで\(\,J\,\)は回転量子数であり、\(\,0\,\)を含む整数のみが許される。すなわち回転エネルギーは量子化されており、飛び飛びの準位のみが許されることになる。\(\,B\,\)は回転定数と呼ばれるもので次式で表される。
\(\quad B=\dfrac{h}{8\pi^2I}\quad\)周波数単位}\(\qquad \dfrac{h}{8\pi^2c_0I}\quad\)波数単位\(\quad\cdots\,\)(2.9)
2-2. 観測される回転スペクトル
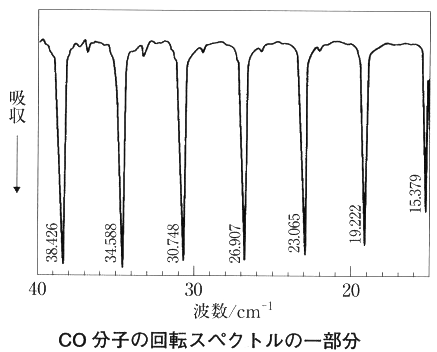 回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。
回転運動だけに起因するスペクトルはマイクロ波領域から遠赤外線領域に現れる。図は期待状態のCO分子の吸収スペクトルである。規則的な間隔の吸収線からなる。式(2.8)より2原子分子の場合の回転エネルギー準位は下図のようになることが理論的に予測できる。
回転量子数の\(\,J=0,1,2,3,\cdots\,\)に対して、エネルギー準位は\(\, 0,2B,6B,12B,\cdots\,\)となる。従って隣接するエネルギー準位間の大きさは \(\,2B,4B,6B,\cdots\,\)である。これを横軸にエネルギーをとってプロットすると図の下に示したようにスペクトルの位置が\(\,2B\,\)の間隔で並ぶ。これは実測のスペクトルとぴったり一致する。
 このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。
このようにして、光子を1つ吸収することによる(2原子分子の)回転遷移は、\(\,J\,\)の値が1つだけ変化する状態の間に起こることがわかる。吸収はエネルギーが増える方向への遷移であるが、エネルギーが減る方向の瀬には発光スペクトルとして観測され、実際同様なスペクトルを示すことがわかっている。すなわち回転遷移の選択則は\(\,\Delta J=\pm 1\,\)である。ここでは、この選択則を実測との対応から導いたが、理論的にも同じ結果が導かれる。
以上のようにして、実測スペクトルの間隔から回転定数\(\,B\,\)が決定できる。この\(\,B\,\)は(2.9)式に定義された量であるから、\(\,B\,\)がわかるということは慣性モーメント\(\,I\,\)が実験的に求められたことを意味する。これより\(\,B\to I\to r\,\)のようにして、分子の構造を与える情報\(\,r\,\)が得られることになる。
2原子分子であるNO分子についても同様な解析が可能であり、実測スペクトルから分子構造に関する情報を導くことができる。それらの結果を以下の表にまとめる。
| \(\mu\) (kg) | 回転定数\(\,B\) (Hz) | \(B\,\)cm\(^{-1}\) | 結合距離 \(r\,\mathring{\mathrm{A}}\) | |
|---|---|---|---|---|
| \(^{12}\)CO | \(1.139\!\times\!10^{-26}\) | \(5.793\times 10^{10}\) | \(1.932\) | \(1.128\) |
| \(^{13}\)CO | \(1.191\!\times\!10^{-26}\) | \(5.538\times 10^{10}\) | \(1.847\) | \(1.128\) |
| NO | \(5.012\!\times\!10^{10}\) | \(1.672\) | \(1.151\) | |
COの場合、\(J\!=\!1\!-\!0\,\)の回転遷移では、\(E=BJ(J+1)\,\) より、\(115.9\)GHz となり、\(^{13}\)COでは、\(110.8\)GHzとなる。\(J\!=\!2\!-\!1\,\)の場合は \(\,6B-2B=4B\,\)なので、\(^{12}\)CO は\(231.7\)GHzで、\(^{13}\)COは\(\,221.5\,\)GHzになる。
2-3. 観測されたスペクトル
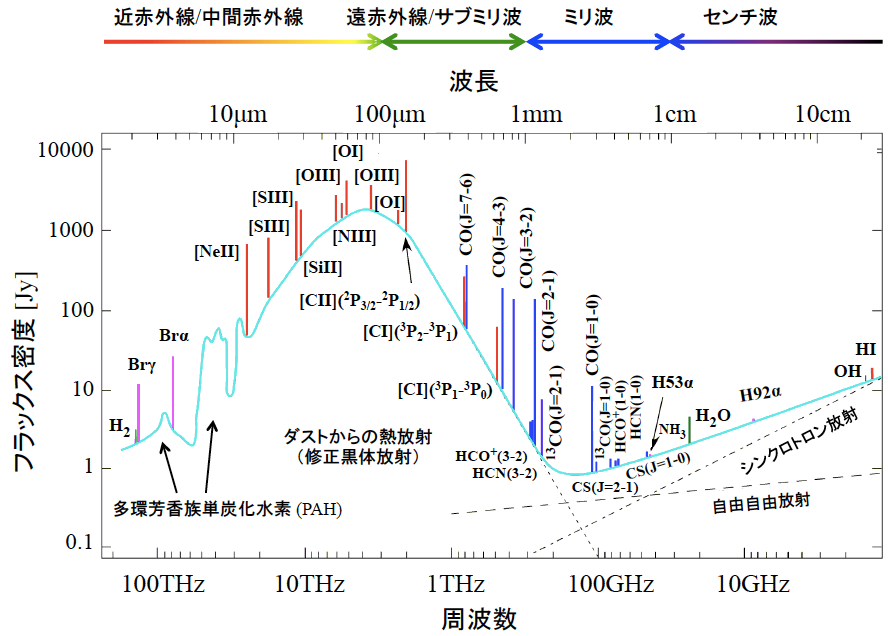
爆発的星形成銀河(starburst銀河)M82の中心数100pc領域における、赤外線から電波に至る波長領域のスペクトル。大別して、(1)周波数に対して、連続的に放射強度が変化している「連続波放射」と、(2)ある特定の周波数でのみ、強い放射を示す「スペクトル線放射」とに分けられる。
連続波放射は、主に波長の長い電波域におけるシンクロトロン放射(磁場の中を高速で運動している電子からの放射)と、サブミリ波~赤外線域にかけて、大きな山をつくっている成分、すなわち、星間ダスト(星間空間中に存在する、シリケイトなどの固体微粒子)からの熱放射の重ね合わせとしてよく説明でできる。
この他、ミリ波付近には自由・自由遷移放射(電離領域中を運動する自由電子からの放射)も見られる。一方、この波長帯のスペクトル線放射としては、原子からの再結合線(桃色)・微細構造線(赤)・超微細構造線、分子からの回転線(青)などがみられる。
|
|
|
|
|