最近、Youtube で流れている問題を見ていると、すっかり忘れている事や知らないことが多い。そこで、いくつかの問題とその解法を備考録に書いていきます。
【問1】
\(\quad\sqrt{3}\sin 2x+2\sin^2x-1\,\) の\(\,0\!\le\!x\!\le\!\pi\,\)での最大値と最小値を求めよ。
【解法】
三角関数って、やっていないと直ぐ忘れる。この場合は倍角の公式を使う。
\(\quad \cos 2\alpha=1-2\sin^2\alpha\qquad\cdots\,\)(1)
これを使うと与式は
\(\quad\sqrt{3}\sin 2x-\cos 2x=2\left(\dfrac{\sqrt{3}}{2}\sin 2x+\left(-\dfrac{1}{2}\right)\cos 2x\right)\,\cdots\,\)(2)
ここで\(\,\sin\,\)の加法定理が
\(\quad\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\qquad\cdots\,\)(3)
であり、\(\cos(-\pi/6)=\sqrt{3}/2\,,\quad\sin(-\pi/6)=-1/2\,\)なので、(2)式は
\(\quad 2\left(\sin 2x\cos\left(-\dfrac{\pi}{6}\right)+\cos 2x\sin\left(-\dfrac{\pi}{6}\right)\right)\qquad\cdots\,\)(4)
(4)と加法定理の(3)を見比べれば
与式は以下のように変形できる。
\(\quad 2\left(\sin\left(2x-\dfrac{\pi}{6}\right)\right)\qquad\cdots\,\)(5)
最大値は\(\,2x-\pi/6=\pi/2\,\)のときなので \(\,\,x=\pi/3\,\)のとき\(\,\,2\)
最小値は\(\,2x-\pi/6=3\pi/2\,\)のときなので \(\,\,x=5\pi/6\,\)のとき\(\,\,-2\)
【問2】
\(\quad x^5+x+1\quad\)を因数分解せよ。
【解法】
ネットでは、まず1の3乗根を使うとあります。これは以下の方程式の
\(\quad x^3-1=(x-1)(x^2+x+1)=0\qquad\cdots\,\)(6)
根は、\(x=1,\,(-1\pm\sqrt{3}\,i)/2\,\)である。
\(\omega=(-1+\sqrt{3}\,i)/2\,\)とすると
\(\quad\omega^2=(-1-\sqrt{3}\,i)/2\,,\quad\omega^3=1\,\)である。
\(\quad\omega^2+\omega+1=0\,\)である。与式に\(\,\omega\,\)を代入すると
\(\quad\omega^5+\omega+1=\omega^2+\omega+1=0\,\)なので割り切れる。
そこで、与式を\(\,x^2+x+1\,\)で割ってみる。
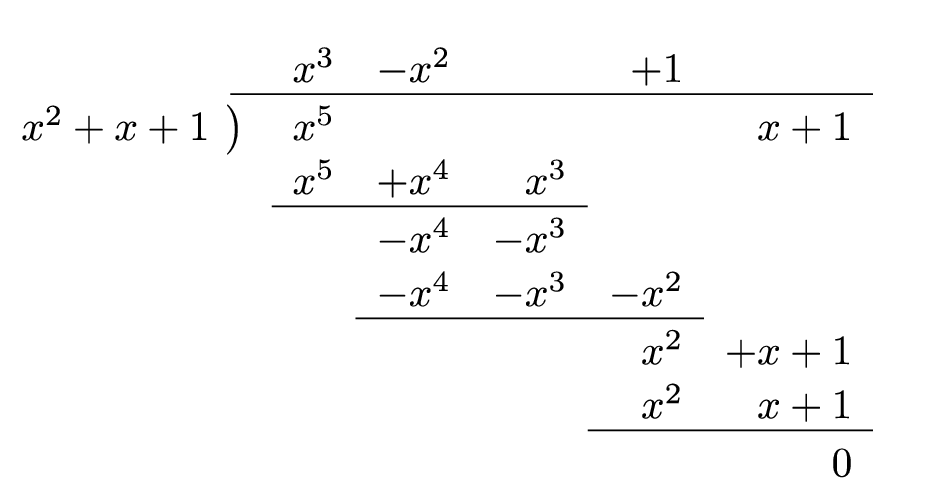
このように、割り切れる。商が\(\,x^3-x^2+1\,\)となるので、答えは
\(\quad x^5+x+1=(x^2+x+1)(x^3-x^2+1)\quad\)となります。
別解(?)として、以下のように展開する方式があります。
\(\quad x^5+x+1=x^5-x^2+x^2+x+1=x^2(x^3-1)+x^2+x+1\)
\(\qquad =x^2(x-1)(x^2+x+1)+x^2+x+1\)
\(\qquad =(x^2+x+1)(x^3-x^2+1)\)
【問3】
\(\quad a^2+b^2=1224\quad\)にあてはまる自然数の組を答えよ。
【解法】
この手の整数の問題は合同式を使うのがセオリーらしい。
\(\,{\large \bigstar\,}\)合同式
一般に、ある2つの整数\(\,a,\,b\,\)を自然数\(\,m\,\)で割った余りが等しいとき、\(a,\,b\,\)は\(\,m\,\)を法として合同であるといい
\(\quad a\equiv b\,(\mathrm{mod}\, m)\qquad\)と表す。
この式のことを合同式といい、\(a-b\,\)が\(\,m\,\)で割りれることを表す。
合同式では加法・減法・乗法が成り立つ。
\(a\equiv b\,(\mathrm{mod}\,m),\,\,c\equiv d\,(\mathrm{mod}\,m)\,\)のとき
\(\quad a+c\equiv b+d\,(\mathrm{mod}\,m)\)
\(\quad a-c\equiv b-d\,(\mathrm{mod}\,m)\)
\(\quad ac\equiv bd\,(\mathrm{mod}\,m)\)
除法については\(\, ac\equiv bc\,(\mathrm{mod}\,m)\,\)で
\(\quad\cdot\,c\,\)と\(\,m\,\)が互いに素のとき、
\(\qquad a\equiv b\,(\mathrm{mod}\,m)\)
\(\quad\cdot\,c\,\)と\(\,m\,\)が互いに素でないとき、\(c\,\)と\(\,m\,\)の最大公約数を\(\,d(>1)\,\)とすると
\(\qquad a\equiv b\,(\mathrm{mod}\,\dfrac{m}{d})\quad\)が成立する。
\(\,{\large \bigstar\,}\)平方剰余と平方数の性質
\(\quad a^2\equiv b\,(\mathrm{mod}\,m)\,\)となる整数\(\,a\,\)が存在するとき、\(b\,\)は\(\,m\,\)を法とする平方剰余であるという。
・平方数に関する重要な性質
\(1\,\):平方数を\(\,3\,\)で割った余りは必ず\(\,0\,\)か\(\,1\,\)。余りが\(\,2\,\)になることはない。
\(2\,\):平方数を\(\,4\,\)で割った余りは必ず\(\,0\,\)か\(\,1\,\)。余りが\(\,2\,\)か\(\,3\,\)になることはない。
これらをふまえて、解法は以下のようになる
\(\,1224=2^3\,3^2\,17\,\)なので
・\(\,a^2+b^2=1224=4\times 306\,\)より
\(\quad a\equiv0\,(\mathrm{mod}\,2)\,\)かつ\(\,b\equiv0\,(\mathrm{mod}\,2)\)
・\(\,a^2+b^2=1224=9\times 136\,\)より
\(\quad a\equiv0\,(\mathrm{mod}\,3)\,\)かつ\(\,b\equiv0\,(\mathrm{mod}\,3)\quad\)なので
\(\therefore\quad a\equiv0\,(\mathrm{mod}\,6)\,\)かつ\(\,b\equiv0\,(\mathrm{mod}\,6)\quad\)となるので
\(\quad a=6x,\,b=6y\,\)とおくと\(\,\,x^2+y^2=34\,\,\)になり、
\(\quad (x,y)=(5,3)\,,\,(3,5)\,\)となるので\(\,(a,b)=(30,18)\,or\,(18,30)\,\)
|
|
|
|
|