ポリトロープとは、熱力学で使うときと天文で使うときで多少感じが違う。まずは、熱力から
● ポリトロープ変化
圧力\( P\)と比容積\( V\)が以下の関係で結ばれる変化をポリトロープ変化という（この変化は可逆変化）
\(\quad PV^n=C\quad n\): ポリトロープ指数
\(\qquad n=0\qquad P=C\quad\,\,\): 等圧変化
\(\qquad n=1\qquad PV=C\quad\): 等温変化
\(\qquad n=\gamma\qquad PV^{\gamma}=C\quad\): 断熱変化
\(\qquad n=\infty\quad\,\, V=C\qquad\): 等積変化
【1】気体の比熱
熱力学の第1法則は
\(\,U\,\)を内部エネルギー、\(\,Q\,\)を熱量、\(\,W\,\)を仕事とすると
\(\quad dU=d’W+d’Q\quad \cdots\)(1)
と表せる。ここで \( d’\,\)は準静的過程を表す。
\(\quad d’W=-PdV\quad \cdots\)(2)
\(\quad dU=-PdV+d’Q\quad \cdots\)(3)
体積が一定として、\(dT\,\)で割ると
\(\quad C_V=\dfrac{d’Q}{dT}=\left(\dfrac{\partial U}{\partial T}\right)_V\quad \cdots\)(4)
同様に、圧力が一定とすれば
\(\quad C_P=\left(\dfrac{\partial U}{\partial T}\right)_P+P\left(\dfrac{\partial V}{\partial T}\right)_P\quad \cdots\)(5)
また、(4)式を \(T\)で積分すると\(\,\,U=C_VT\quad \cdots\)(6)
1モルでは \(\,\,PV=\mathrm{R}T\quad \cdots\)(7)\(\,\,\)で
\(\quad P\left(\dfrac{\partial V}{\partial T}\right)_P=\mathrm{R}\quad \cdots\)(8) なので、(5)式は
\(\quad C_P=C_V+\mathrm{R}\quad \cdots \)(9)
【2】断熱変化
\(dU\,\)の微分を考える
\(\quad dU=\left(\dfrac{\partial U}{\partial T}\right)_VdT+\left(\dfrac{\partial U}{\partial V}\right)_TdV\quad \cdots\)(10)
これを(3)式に代入すると
\(\quad d’Q=\left(\dfrac{\partial U}{\partial T}\right)_VdT+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]dV\quad \cdots\)(11)
\(P=\)一定として(11)式を\(dT\,\)で割ると
\(\quad C_P=C_V+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]\left(\dfrac{\partial V}{\partial T}\right)_P\quad \cdots\)(12)
断熱変化では \(d’Q=0\,\)なので(11)式は
\(\quad \left(\dfrac{\partial U}{\partial T}\right)_VdT+\left[P+\left(\dfrac{\partial U}{\partial V}\right)_T\right]dV=0\quad \cdots\)(13)
理想気体では\(\,(U\,\)は温度だけの関数なので \(\left(\dfrac{\partial U}{\partial V}\right)_T=0\)
(13)式に(6)式と(7)式を代入すると
\(\quad C_VdT+\dfrac{\mathrm{R}T}{V}dV=0\quad \cdots\)(14)
比熱比を\(\,\gamma=\dfrac{C_P}{C_V}\quad \cdots\)(15)\(\quad\)として(14)式を\(C_VT\,\)で割ると
\(\quad \dfrac{dT}{T}+(\gamma-1)\dfrac{dV}{V}=0\quad \cdots\)(16)\(\quad\)なので
\(\quad \ln T+(\gamma-1)\ln V= \text{一定} \cdots\)(17)\(\quad\)よって
\(\quad TV^{\gamma-1}= \text{一定} \cdots\)(18)
式(7)より\(\quad T=\dfrac{PV}{\mathrm{R}}\quad\cdots\)(19)を代入すると
\(\quad PV^{\gamma}=\text{一定}\quad \cdots\)(20)「ポアソンの法則」が得られる。
常温での\(\,C_V\,\)は並進運動と回転運動の自由度の\(\frac{\mathrm{R}}{2}\,\)倍となる。
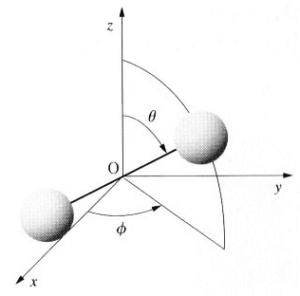単原子分子では並進運動の自由度が３なので、\(\,C_V=\frac{3}{2}\mathrm{R}\)。
２原子分子では\(\theta\,,\,\phi\,\)の回転が加わり、自由度が５になるので、\(\,C_V=\frac{5}{2}\mathrm{R}\)となる。
３原子分子(直線形)では、並進の自由度と回転の自由度は、２原子分子と同様だが振動の自由度が4となる。この振動は常温での比熱に寄与しないので、\(\,C_V\,\)は同じとなる。
よって、単原子分子は \(\gamma=\frac{5}{3}\,\)となり、２原子分子と直線形の３原子分子は \(\,\gamma=\frac{7}{5}\,\)となる。
 |
 |
 |